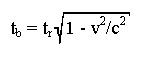Visits: 2225
Philipp Wehrli, 2. Januar 2002,
ergänzt um den Abschnitt Überlichtgeschwindigkeit und Zeitreisen am 18. Oktober 2011
Einsteins berühmte Relativitätstheorie revolutionierte unsere Vorstellung von Raum und Zeit. Die spezielle Relativitätstheorie beschreibt die Bewegungen im gravitationsfreien Raum, während die allgemeine Relativitätstheorie die Gravitation als ein Phänomen erklärt, das durch die Krümmung der Raumzeit entsteht. Hier werden einige der wichtigsten Phänomene der speziellen Relativitätstheorie vorgestellt: Die Verlangsamung von bewegten Uhren (Zwillingsparadoxon), die Längenkontraktion und die Magnetkraft.
1. Die Suche nach dem Äther
2. Die Idee der speziellen Relativitätstheorie
3. Zeitdilatation
4. Experimente zur Uhrenverlangsamung
5. Das Zwillingsparadoxon
6. Was heisst ‘gleichzeitig’?
7. Längenkontraktion
8. Magnetismus als Folge der Längenkontraktion
9. Längenkontraktion fotografiert
10. E=mc2
11. Das Minkowski-Diagramm
12. Überlichtgeschwindigkeit und Zeitreisen
13. Weiterführende Literatur
1. Die Suche nach dem Äther
Ende des 19 Jh. zweifelte niemand daran, dass Licht eine Welle ist, die durch die Gleichungen von James Clerk Maxwell beschrieben wurde. Eine Welle braucht aber immer ein Medium, in dem sie sich ausbreiten kann. So ist es z. B. auf dem Mond unmöglich zu sprechen, weil der Mond keine Atmosphäre hat, welche die Schallwellen tragen könnte. Die Physiker glaubten daher, das ganze Universum sei von einem sogenannten Äther überflutet, durch den die Lichtwellen wogen. Dieser Äther kommt eigenartigerweise in den Maxwell-Gleichungen nicht vor. Das scheint absurd: Wenn ich einer Welle entgegeneile, sollte sich die Welle mir schneller nähern. Die Geschwindigkeit der elektromagnetischen Wellen war aber nach den Maxwell-Gleichungen weder abhängig von der Geschwindigkeit des Beobachters, noch von der Geschwindigkeit der Quelle. Es war deshalb eine wichtige Aufgabe, den Äther zu messen und die Korrektur in die Maxwell-Gleichungen einzufügen. Die Sache wurde noch verwirrender dadurch, dass alle Experimente die scheinbar absurden Maxwell-Gleichungen bestätigten. Der Äther war nicht messbar!
Weil die Erde um die Sonne kreist, während der vermutete Äther in Ruhe ist, bewegt sich die Erde zumindest die meiste Zeit relativ zum Äther. Dies sollte eine ganze Reihe von messbaren Effekten zur Folge haben und gegen Ende des 19 Jh. und Anfangs des 20 Jh. versuchten die Physiker in verschiedenen Experimenten vergebens, diese Effekte nachzuweisen.
Z. B. sollte die Lichtbrechung in Glas davon abhängig sein, wie das Glas relativ zur Bewegungsrichtung der Erde durch den Äther ausgerichtet ist. Dazu machten 1860 Fizeau, 1872 Mascart und 1902 Lord Rayleigh Versuche, ohne den Effekt nachweisen zu können. Auch müssten sich die Platten eines Kondensators stets normal zur Richtung der Erdbewegung durch den Äther ausrichten. Dies versuchten Trouton und Noble erfolglos zu messen.
Berühmt wurde ein Experiment, das Albert Michelson und Edward Morley 1886 durchführten. (Historisch spielte dieses Experiment zwar nicht die herausragende Rolle, die ihm heute eingeräumt wird.) Michelson und Morley sagten sich: Wenn die Erde den Lichtwellen entgegeneilt, müsste die auf der Erde gemessene Lichtgeschwindigkeit grösser sein, als wenn die Erde von der Welle davoneilt. Völlig überraschend zeigte sich aber, dass die Lichtgeschwindigkeit c auf der Erde in allen Richtungen unabhängig von Tages- oder Jahreszeiten immer gleich gross ist (Sex 2).
Abbildung 1 Wird aus dem mittleren Fenster eines fahrenden Schiffes ein Stein geworfen, dann erreichen seine Wellen zuerst den hinteren Teil des Schiffes und erst später den vorderen. Albert Michelson und Edward Morley zeigten, dass bei Lichtwellen keine solchen Effekte zu beobachten sind.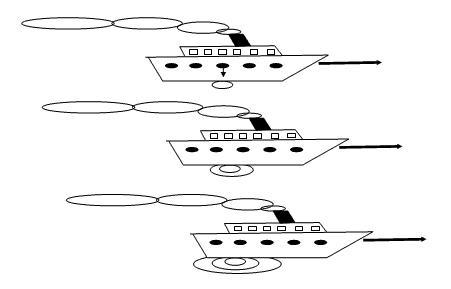
2. Die Idee der speziellen Relativitätstheorie
Diese Resultate wurden intensiv diskutiert. Man überlegte sich z. B., ob vielleicht die Erde von einem Ätherwirbel umhüllt sein könnte. Aber letztlich mussten alle diese Hypothesen wieder verworfen werden, weil sich immer ein Experiment fand, dem sie widersprachen.
Schliesslich hatte Albert Einstein 1905 die Idee, dass wir den Äther vielleicht deshalb nicht messen können, weil es den Äther nicht gibt. Er analysierte die Begriffe ‘Weg’, ‘Zeit’ und ‘Bewegung’ sehr sorgfältig und achtete strikte darauf, nur von Dingen zu sprechen, die wir auch tatsächlich messen können. Einstein baute seine Theorie auf zwei Prinzipien, von denen er annahm, dass sie immer gelten:
1) Die Naturgesetze sind für alle unbeschleunigt bewegten Beobachter gleich.
2) Die Lichtgeschwindigkeit c beträgt für alle Beobachter 299’792 km/s, unabhängig davon, wie sich die Lichtquelle oder der Empfänger bewegen.
Das erste, das sogenannte Relativitätsprinzip gilt schon in Newtons Physik. ‘Relativ’, weil es kein absolutes Ruhesystem gibt, für das spezielle Gesetze gelten. Bewegung ist nur relativ zu einem anderen Körper definierbar, aber nicht zu einem ruhenden Raum. Wenn Einstein den Begriff ‘relativ’ brauchte, meinte er nicht: „Ein Schnellzug ist relativ schnell im Vergleich mit einer Schnecke.“ Dieses ‘Relativ’ würde ja genau das absolute Ruhesystem voraussetzen, das Einstein ausmerzen wollte. Einstein meinte mit ‘relativ’ etwas ganz anderes, nämlich: „Der Zug hat eine hohe Geschwindigkeit relativ zur Schnecke und die Schnecke hat eine hohe Geschwindigkeit relativ zum Zug.“
‘Relativ’ bedeutet ‘in Bezug auf.’ Damit ist gemeint: Aus Sicht des Zugpassagiers flitzt die Schnecke wahnsinnig schnell am Fenster vorbei. Ob sich der Zug relativ zur Erde bewegt oder ob die Schnecke am Fenster vorbei katapultiert wird, darüber sagt dieser Satz nichts. Das Relativitätsprinzip sagt, um anzugeben, wie schnell sich ein Körper bewegt, muss ich angeben, relativ zu welchem Bezugssystem die Geschwindigkeit gemessen wird. Übrigens galt dieses Relativitätsprinzip schon bei Newton.
Erst Einsteins zweites Prinzip unterscheidet sich von Newtons Physik. Es wird das Prinzip von der Konstanz der Lichtgeschwindigkeit genannt. Dieses Prinzip sagt, dass nicht alles relativ ist. Die Lichtgeschwindigkeit ist absolut, also für alle Beobachter gleich. Einstein nannte seine Theorie deshalb zuerst ‘Absolutheitstheorie’. Denn dieser Punkt war der eigentlich neue.
Ebenso wie das Licht bewegen sich übrigens alle anderen elektromagnetischen Wellen im Vakuum mit der Lichtgeschwindigkeit c, also z. B. auch Radiowellen, Mikrowellen und UV-Strahlen. Weil die Atomuhren auf der Erde und in Satelliten heute mit Radiosignalen synchronisiert werden, würde es sofort auffallen, wenn Radiowellen irgendwo schneller oder langsamer wären.
3. Zeitdilatation
Wie kann es geschehen, dass die Lichtgeschwindigkeit für alle Beobachter gleich gross ist? Wenn ich einer Lichtquelle entgegenfahre, müsste mir das Licht doch schneller erscheinen! Genau dies wird aber nicht gemessen. Irgendetwas stimmt also mit der Geschwindigkeitsmessung nicht oder mit unserer Interpretation der Geschwindigkeitsmessung.
Einstein überlegte sich sehr genau, wie wir die Lichtgeschwindigkeit überhaupt messen. Wenn wir die Lichtgeschwindigkeit messen, messen wir eine Strecke und wir messen die Zeit, die das Licht braucht, um diese Strecke zurückzulegen. Wenn die Lichtgeschwindigkeit für alle Beobachter gleich gross ist, heisst dies, dass die Beobachter die Zeit oder den Weg oder beides unterschiedlich messen.
Die Zeit könnten wir z. B. mit der folgenden Lichtuhr messen: Ein Lichtimpuls wird durch ein Rohr geschickt und am anderen Ende gespiegelt. Wenn das Licht wieder am Boden ankommt, soll die Uhr gerade zwei Nanosekunden (2 ns) zeigen. Für den ruhenden Beobachter ist das Licht nach 1 ns beim Spiegel.
Wird die Lichtuhr bewegt, so muss das Licht vom ruhenden Beobachter aus gesehen einen weiteren Weg zurücklegen. Wenn die ruhende Uhr 1 ns zeigt, ist das Licht bei der bewegten Uhr noch nicht beim Spiegel angekommen. Die bewegte Uhr zeigt also noch nicht eine Nanosekunde. Die bewegte Uhr läuft langsamer.
Abbildung 2 In einer ruhenden Lichtuhr kommt der Lichtimpuls nach einer Nanosekunde oben an und schaltet die Uhr eine Nanosekunde weiter. In einer bewegten Uhr hat der Lichtimpuls nach einer Nanosekunde erst einen Teil der Strecke zurückgelegt. Die bewegte Uhr geht deshalb langsamer.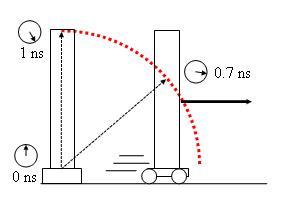
Im Ruhesystem wird also eine andere Zeit gemessen als im bewegten System. Ich nenne die Zeit im Ruhesystem tr. Die Zeit im bewegten System nenne ich die Eigenzeit tb des bewegten Beobachters. Die Eigenzeit einer Uhr ist also immer die Zeit, welche die Uhr anzeigt (sofern sie nicht kaputt ist).
Ich möchte nun die Idee der speziellen Relativitätstheorie in einem etwas speziellen Raum-Zeit-Diagramm zeichnen. Diese Darstellung ist unüblich, aber sehr anschaulich. Wie sie in die üblicherweise verwendete Minkowski-Metrik umgerechnet werden kann, zeigt (Eps 1). Die Relativitätstheorie zeigt, dass Zeit und Raum grosse Ähnlichkeit haben. Damit diese Ähnlichkeit sichtbar wird, multipliziere ich alle Zeiten mit der Lichtgeschwindigkeit c. Denn so kann ich die Zeiten in Metern angeben und mit den Längen vergleichen. Mit diesen Definitionen zeichne ich noch einmal die Abbildung 2, diesmal als Weg-Zeit-Diagramm.
Abbildung 3 Weg-Eigenzeit-Diagramm für eine ruhende Uhr (senkrechter dicker Pfeil) und eine bewegte Uhr (schiefer dicker Pfeil). Wir könnten sagen: Beide Uhren bewegen sich mit Lichtgeschwindigkeit c durch die Raum-Zeit. Wir sehen aber nur die Bewegung im Raum. Die ruhende Uhr bewegt sich nur durch die Zeit. Die bewegte Uhr bewegt sich teilweise durch den Raum, dafür umso langsamer in der Zeit.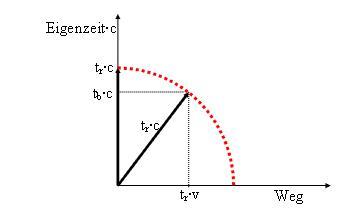
Für Physiker: Dieses Diagramm ist kein Minkowski-Diagramm. Die y-Achse zeigt die Eigenzeit der bewegten Uhr.
Mit dem Satz von Pythagoras folgt aus Abbildung 3 sogleich:
(tr·c)2 = (tb·c)2 + (tr·v)2
Oder nach tb umgestellt:
Das heisst: Wenn eine ruhende Uhr die Zeit tr anzeigt, dann zeigt eine Uhr, die mit der Geschwindigkeit v bewegt wird, die Zeit tb. Bewegte Uhren laufen langsamer! Diesen Effekt nennt man Dilatation der Zeit. Einige Experimente, in denen dies tatsächlich gemessen wird, stelle ich im nächsten Abschnitt vor.
4. Experimente zur Uhrenverlangsamung
Aus dem Alltag sind wir gewohnt, dass unsere Uhren immer gleich schnell laufen, egal was wir tun. Erst wenn die Batterie verbraucht ist oder die Uhr kaputt geht, stimmt dies nicht mehr. In Wirklichkeit stimmt dies aber nicht exakt. Wenn ich zwei exakt gleiche und absolut präzise Uhren im Punkt A exakt gleich stelle und sie danach auf verschiedenen Wegen zu einem Punkt B trage, dann zeigen sie nicht mehr unbedingt die gleiche Zeit an. Dabei können die Punkte A und B auch identisch sein. Dieser Effekt wird in den Relativitätstheorien beschrieben, die Albert Einstein in den Jahren 1905 und 1914-1916 formulierte. Dabei sind die folgenden zwei Effekte zu unterscheiden:
1.) Schnell bewegte Uhren gehen langsamer.
2.) Uhren im Gravitationsfeld, also in der Nähe einer grossen Masse gehen langsamer.
Der erste Effekt wird durch die spezielle, der zweite durch die allgemeine Relativitätstheorie erklärt. Das Experiment wurde hundertfach und mit völlig verschiedenen Uhren durchgeführt. Alle Uhren gehen langsamer, wenn sie bewegt sind, und sie laufen alle nach den gleichen Gesetzen, die Einstein in der Relativitätstheorie vorhersagte. Messbar wird dies allerdings erst, wenn die Bewegung sehr schnell, wenn möglich fast mit Lichtgeschwindigkeit erfolgt. Vier solche Experimente möchte ich kurz schildern.
Weil die Versuche mit völlig verschiedenen Uhren funktionieren, nehmen die Physiker an, dass auch für Lebewesen die Zeit langsamer läuft, wenn sie schnell bewegt werden. D. h. die Passagiere haben während des Fluges mit hoher Geschwindigkeit auch weniger Zeit, sich Gedanken zu machen oder sich zu langweilen. Wenn ein Zwilling in Ruhe auf der Erde bleibt, während sein Zwillingsbruder annähernd mit Lichtgeschwindigkeit eine weite Reise macht, wird der Zwilling auf der Erde bei der Rückkehr des anderen viel älter sein als jener. Bei einem gewöhnlichen Flug mit gewöhnlichen Uhren ist der Effekt natürlich nicht messbar, weil die Geschwindigkeit viel zu klein ist.
1.) 1972 führten Joseph Hafele und Richard Keating mehrere Experimente mit zwei genau gleichen Cäsium-Atom-Uhren durch. Sie stellten die beiden Uhren exakt gleich und legten dann die eine in ein Flugzeug, das einmal um die Erde flog. Als das Flugzeug wieder zurückkehrte, verglichen sie die Uhren miteinander. (Sex 2) oder (Sex 3)
Bei diesem Experiment muss berücksichtigt werden, dass die Uhren, welche auf der Erde zurückgelassen werden, nicht in Ruhe sind. Sie werden vielmehr mit der Erdrotation mitgedreht. Die Uhren, welche die Erde in östlicher Richtung umkreist hatten, bewegten sich weniger als die Uhren auf der Erde. Sie gingen um 273±7 Nanosekunden vor. Die Uhren, die in westlicher Richtung flogen, gingen um 59±10 Nanosekunden nach, weil sie schneller bewegt wurden als die Uhren auf der Erde. Die Resultate stimmen exakt mit Einsteins Theorie überein.
2.) Die Verlangsamung der Zeit spielt in der Raumfahrt eine grosse Rolle. Bei Satelliten und Raumsonden ist es enorm wichtig, dass die Uhren sehr exakt stimmen, weil sonst die Navigation nicht funktionieren oder zuviel Energie kosten würde. Ausserdem haben diese Sonden oft grosse Geschwindigkeiten. Aus diesen Gründen wird der Effekt der Zeitverlangsamung in der Raumfahrt täglich sehr genau gemessen, wobei immer eine exakte Übereinstimmung mit Einsteins Theorie gefunden wurde.
3.) Wenn Teilchen aus dem Weltall auf die Atmosphäre prallen, entstehen spezielle Teilchen, die Myonen. Man kann solche Teilchen auch im Labor herstellen und weiss von da, dass diese in sehr kurzer Zeit zerfallen. Eigentlich zerfallen die Myonen so schnell, dass sie den langen Weg durch die Atmosphäre niemals ganz zurücklegen könnten, selbst wenn sie ungeheuer schnell fliegen würden. Dennoch treffen die Myonen fast alle unversehrt auf dem Erdboden auf. Was ist geschehen?
Weil die Myonen sehr schnell fliegen, steht ihre Zeit fast still. Sie zerfallen deshalb viel langsamer und können dadurch auch den weiten Weg durch die Atmosphäre überstehen. (Sex 2)
4.) Genau das Gleiche kann täglich in vielen Teilchenbeschleunigern auf der ganzen Welt beobachtet werden. Die Teilchenphysiker haben es oft mit Teilchen zu tun, die sehr rasch in andere Teilchen zerfallen. Sie befinden sich deshalb in einer sehr ähnlichen Lage, wie Jasmin mit dem toten Zwilling. Sie müssen versuchen, die Zerfallszeit irgendwie zu verlangsamen, damit sie mehr Zeit für ihre Messung haben. Dies machen sie wie Jasmin so, dass sie die Teilchen auf ihre Achterbahn schicken. Das sind oft kilometerlange Teilchenbeschleuniger, wie etwa das Cern in Genf. Allerdings fliegen die Teilchenphysiker anders als Jasmin bei ihren Experimenten nicht mit den untersuchten Teilchen mit. (Sex 2)
Die Verlangsamung der Zeit ist etwas sehr Seltsames, und vielleicht denken Sie jetzt: Das verstehe ich nicht! Es gibt auch gar nicht viel zu verstehen. Aufgrund der geschilderten Experimente können wir nur sagen, dass die Welt eben so seltsam ist. Wenn Sie sich weiter mit der Relativitätstheorie auseinandersetzen, werden Sie feststellen, dass diese Seltsamkeit der Natur zu keinen logischen Widersprüchen führt und dass sie sich sogar in eine äusserst elegante Theorie zusammenfügt. Mehr verstehen auch die Experten heute nicht. Aber auch wenn wir nicht verstehen, weshalb die Natur so seltsam ist, dürfen wir uns ja doch darüber wundern und daran freuen, nicht wahr?
5. Das Zwillingsparadoxon
Wenn aber die eine Uhr langsamer geht als die andere, ist dies denn nicht ein Verstoss gegen das Relativitätsprinzip? Das System, in dem die Uhren am schnellsten gehen, könnte ich das Ruhesystem nennen. In diesem Ruhesystem wären die Naturgesetze anders als in allen bewegten Systemen, denn zumindest die Uhren würden hier schneller laufen.
Dieser Einwand ist bekannt unter dem Namen ‘Zwillingsparadoxon’. Zwei Zwillinge fahren beide in Raketen mit hoher Geschwindigkeit aneinander vorbei. Jeder Zwillingsbruder würde sagen, der andere sei bewegt und bleibe deshalb jünger. Wer hat recht?
Schauen wir noch einmal in einem Diagramm an, was eigentlich geschieht. In Abbildung 3 wurde willkürlich ein Ruhesystem gewählt. Angenommen, eine Reihe von Beobachtern sitzen in diesem Ruhesystem und beobachten eine bewegte Uhr. Nach jeder Sekunde, die im Ruhesystem vergeht, zeichnet der Beobachter, welcher der Uhr am nächsten ist, im Raumzeit-Diagramm den Punkt ein, an dem sich die Uhr gerade befindet und die Zeit, die sie anzeigt. Die so eingezeichneten Punkte hätten regelmässige Abstände von einer Lichtsekunde.
Abbildung 4 Für drei Uhren a, b und c trage ich nach jeder Sekunde (gemessen mit einer Uhr im Ruhesystem) einen Punkt in das Diagramm. Die Eigenzeitachse zeigt die Zeit, welche die Uhr zum Zeitpunkt der Eintragung anzeigt. Die Skala ist so gewählt, dass sich die Spuren aller Uhren im Raumzeit-Diagramm gleich schnell ausbreiten. Eine Uhr, die sich schnell durch den Raum bewegt, bewegt sich weniger schnell durch die Zeit.
Im Diagramm in Abbildung 4 wurde aber wieder willkürlich ein Ruhesystem gewählt, nämlich das, in dem die Uhr c ruht. Im Ruhesystem a und b würde die Situation analog aussehen: Jeder Beobachter hat das Gefühl, er sei in Ruhe und seine Uhr laufe am schnellsten. Wer hat recht?
Ganz einfach: Sie sollen zusammenkommen und ihre Uhren vergleichen! Um dies zu tun, muss aber mindestens der eine Zwilling seine Rakete wenden. Er fliegt also nicht mehr mit gleichbleibender Geschwindigkeit, sondern er ist beschleunigt. Deshalb gilt für ihn auch das Relativitätsprinzip nicht, das ja besagt: Die Naturgesetze sind für alle unbeschleunigt bewegten Beobachter gleich. Wenn nur der eine Zwilling seine Rakete wendet, dann läuft seine Uhr langsamer. Dies wurde auch beim Mondflug so gemessen. Allerdings betrug der Zeitunterschied nach dreitägiger Fahrt nur Bruchteile einer Sekunde.
Abbildung 5a) Die Spuren von zwei Uhren a und b breiten sich gleich schnell im Raumzeit-Diagramm aus. Weil die Uhren aber nicht nebeneinander liegen, kann nicht entschieden werden, ob eine davon schneller läuft und wenn ja, welche.
b) Damit die Uhren verglichen werden können, muss die eine davon beschleunigt werden. Für diese gilt das Relativitätsprinzip nicht.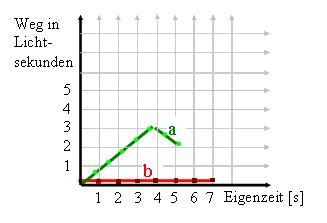
c) Wenn die Uhr a zurückkehrt, zeigt sie erst die Eigenzeit 8s an, während die Uhr b bereits bei 10s ist.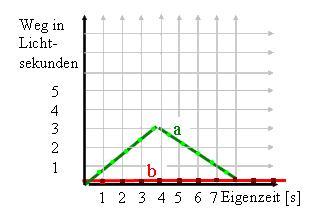
Details zu dieser und vielen anderen scheinbaren Paradoxien aus der Relativitätstheorie hat Jürgen Brandes in einem schönen Buch gesammelt. (Bra 1)
Achtung: Es gibt zwei Sorten der Uhrenverlangsamung, die nicht verwechselt werden dürfen. Uhren laufen langsamer, wenn sie schnell bewegt werden. Und Uhren laufen langsamer, wenn sie in der Nähe einer grossen Masse sind. Der erste Effekt wird in der speziellen Relativitätstheorie erklärt, der zweite in der allgemeinen Relativitätstheorie. Natürlich laufen Uhren auch langsamer, wenn sie kaputt sind oder wenn die Batterie abgelaufen ist, aber dies ist hier selbstverständlich nicht gemeint.
6. Was heisst ‘gleichzeitig’?
Stellen wir uns vor, die Physikerin Anna sitzt in einem Eisenbahnwagen und hat an beiden Enden dieses Wagens eine Uhr aufgestellt, nennen wir sie Uhr A und Uhr B. Anna kriegt die Aufgabe diese beiden Uhren ganz genau gleich richten. Vielleicht denken Sie: „Ok, dann muss sie nur zur Uhr A gehen und von dort aus schauen, welche Zeit die Uhr B zeigt. Diese Zeit stellt sie dann auch bei der Uhr A ein.“
Aber das Licht braucht ja eine gewisse Zeit, um von B zu A zu kommen. Nach der vorgeschlagenen Methode würde also die Uhr A nachgehen.
„Nun gut“, sagen Sie vielleicht, „Dann trägt sie eben die Uhr A zur Uhr B und stellt sie dort ein. Danach trägt sie sie wieder zurück.“ Aber mit diesem Herumtragen von Uhren sollten wir vorsichtig sein. Irgendwie stimmt ja etwas mit den Uhren in den fahrenden Raketen nicht. Wir sollten daher die Uhren so wenig wie möglich bewegen, wenn wir sie richten wollen.
Albert Einstein machte den folgenden Vorschlag: Anna soll eine Lampe in die Mitte des Wagens stellen. Sie lässt diese Lampe kurz aufleuchten, und wenn das Licht bei den Uhren ankommt, sollen die Uhren zu laufen beginnen. Diese Methode wird die „Einsteinsche Uhrensynchronisation“ genannt.
Nun nehmen wir an, der Physiker Berti fahre in einem zweiten genau gleichen Zug, ebenfalls mit zwei Uhren C und D an Anna vorbei. Und wir lassen die Lampe genau in dem Moment aufblitzen, in dem die beiden Zugsmitten nebeneinander liegen. Anna beschreibt den Vorgang so: Ich bin in Ruhe, Berti fährt an mir vorbei. Die Lampe leuchtet auf. Etwas später kommt das Licht bei der Uhr D an und schaltet diese ein. Dann erreicht das Licht gleichzeitig A und B, wobei auch diese Uhren zu laufen beginnen. Und am Schluss wird auch noch C gestartet.
Abbildung 6 Einsteinsche Uhrensynchronisation. Zwei Uhren werden synchronisiert, indem man genau in die Mitte zwischen ihnen eine Lampe aufblitzen lässt. Wenn der Blitz bei den Uhren ankommt, beginnen diese zu laufen.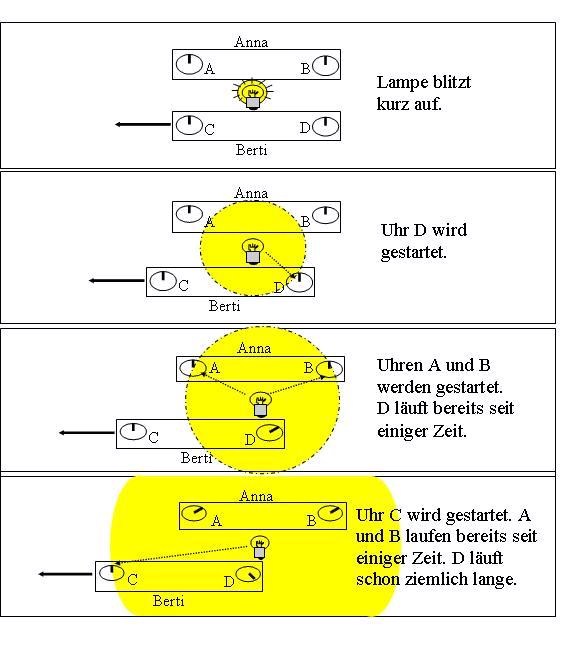
Berti ist mit dieser Schilderung überhaupt nicht einverstanden. Er sagt: „Ich bin in Ruhe, Anna fährt an mir vorbei. Die Lampe leuchtet auf. Zuerst kommt das Licht bei der Uhr A an, denn diese Uhr fährt ja dem Licht entgegen. Dann erreicht das Licht gleichzeitig C und D. Selbstverständlich gleichzeitig, denn C und D waren ja die ganze Zeit gleich weit von der Lampe entfernt. Die Uhr B wird erst Schluss gestartet, denn B fährt ja den Lichtwellen davon.“
Wenn für Anna zwei Ereignisse gleichzeitig, aber an verschiedenen Orten stattfinden, dann sind sie für Berti nicht gleichzeitig. Wer hat recht? -Nach dem Relativitätsprinzip sind die Beobachtungen von Anna und Berti gleichwertig. Beide haben recht. Gleichzeitigkeit an verschiedenen Orten ist relativ, also abhängig vom Beobachter. Wenn aber ein Ereignis 1 ein Ereignis 2 verursacht, dann liegt für alle Beobachter 1 in der Vergangenheit von 2. Physiker sagen: Kausalitätsbeziehungen sind absolut.
Dies hat zur Folge, dass Erhaltungssätze immer lokal gelten müssen. Wenn z. B. die elektrische Ladung erhalten bleibt, bedeutet dies, dass nicht am Ort A eine Ladung verschwinden kann, um gleichzeitig dafür an einem anderen Ort B wieder aufzutauchen. Denn wenn dies geschehen würde, dann gäbe es ein anderes Bezugssystem, in dem dieses ‘gleichzeitig’ nicht mehr gleichzeitig wäre. In diesem anderen Bezugssystem würde dann eine Zeitlang eine Ladung fehlen oder es wäre eine Ladung zuviel da.
7. Längenkontraktion
In Abschnitt 4 erwähnte ich Myonen, die in der obersten Atmosphärenschicht entstehen und die Erde erreichen, obwohl sie eigentlich viel früher zerfallen müssten. Wie schaffen es die Myonen, den sehr weiten Weg durch die Atmosphäre zurückzulegen?
Wir, die wir auf der Erde stehen und zuschauen, sagen, die Zeit der Myonen läuft langsamer, weil die Myonen sehr schnell fliegen. Die Geschwindigkeit der Myonen ist aber nur relativ zu uns sehr gross. Ein Myon, das mitfliegt, würde sagen, die Myonen sind alle in Ruhe, aber die Erde bewegt sich ungeheuer schnell auf die Myonen zu. Für die Myonen selbst läuft deshalb die Zeit völlig normal. Trotzdem wissen auch die Myonen, dass sie keinen sehr weiten Weg zurücklegen können und auch die Myonen stellen fest, dass sie schliesslich auf der Erde landen und nicht schon vorher zerfallen. Wie würden die Myonen dies erklären?
Die Myonen würden sagen: „Wir waren nur ganz kurze Zeit in der Atmosphäre, so kurz, dass wir auf der Erde aufschlugen, bevor wir von selbst zerfielen.“ Und sie sagen weiter: „Der Weg durch die Atmosphäre war sehr kurz. Weil sich die Erde auf uns zu bewegte, wurde dieser Weg zusammengedrückt.“
8. Magnetismus als Folge der Längenkontraktion
Wie lässt sich dieses ‘Zusammendrücken’ des Weges in der Natur beobachten? Den schönsten relativistischen Effekt kennen Sie aus dem Alltag: Es ist die elektromagnetische Kraft, die jeden Elektromotor antreibt. Wie Sie wissen, ziehen sich eine positive und eine negative Ladung an. Und wie Sie ebenfalls wissen, besteht ein stromdurchflossener Leiter aus Atomen mit positiv geladenen Kernen, in dem ein Teil der Elektronen, also negative Ladungen fliessen. Wenn in einem ungeladenen Leiter Strom fliesst, sind die positiven und die negativen Ladungen ausgeglichen. D. h., auf eine ruhende elektrische Ladung neben dem Leiter wirkt keine Kraft.
Abbildung 7 Ein ungeladener Leiter, in dem Strom fliesst. Die negativen und die positiven Ladungen im Leiter sind genau ausgeglichen. Auf eine negative Probeladung neben dem Leiter wirkt keine Kraft. Das e- steht für Elektron.
Schauen wir nun, was geschieht, wenn die negative Probeladung in die gleiche Richtung fliegt wie die Elektronen im Leiter. Von der bewegten Probeladung aus gesehen, sind die positiven Ladungen im Leiter nun bewegt, sie liegen also wegen der Lorentzkontraktion näher beieinander. Die negativen Ladungen im Leiter, die vorher bewegt erschienen, sind nun relativ zur Probeladung nicht mehr bewegt. Wenn diese vorher eine Lorentzkontrahiert waren, sind sie es nun für die mitbewegte Ladung nicht mehr. Das Elektron, das neben dem Leiter bewegt wird, sieht also die positiven Ladungen dichter und die negativen weniger dicht beieinander. Der Leiter, der im Ruhesystem ungeladen ist, erscheint für das bewegte Elektron geladen. Eine Rechnung zeigt, dass dieser Effekt gerade die Ursache der bekannten Lorentzkraft ist (Sex 2). So ergibt sich aus der speziellen Relativitätstheorie von selbst eine Verbindung zwischen Elektrizität und Magnetismus, die in der klassischen Physik völlig unerklärt bleibt.
Abbildung 8 In einem Leiter fliessen negativ geladene Elektronen nach rechts (weil die Pioniere der Elektrizität das früher noch nicht wussten, sagt man in diesem Beispiel unglücklicherweise, “der Strom fliesst nach links”. Wenn ein Elektron neben dem Leiter ebenfalls nach rechts fliegt, sieht es die Abstände zwischen den positiv geladenen Protonen im Leiter kleiner. Der Abstand zwischen den Elektronen im Leiter, die sich in die gleiche Richtung bewegen wie das Elektron aussen, scheinen nun grösser. Dadurch erscheint der Leiter für das neben dem Leiter bewegte Elektron positiv geladen. Durch die Längenkontraktion sieht das Elektron beim Leiter einen Überschuss positiver Ladungen und wird von diesem angezogen. Diese sogenannte elektromagnetische Kraft oder Lorentzkraft folgt also direkt aus der speziellen Relativitätstheorie.
Umgekehrt wird der Elektromagnetismus ja in den Maxwellschen Gleichungen beschrieben. Die Maxwell-Gleichungen sind also relativistisch und müssen nicht abgeändert werden.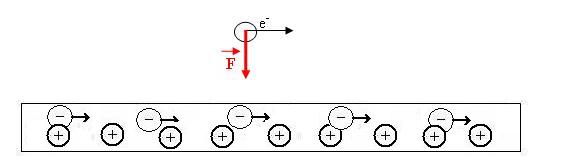
Vielleicht sagen Sie jetzt: „Der Leiter ist doch jetzt positiv geladen. Weshalb wirkt die Lorentzkraft nur auf bewegte Elektronen?” Aber diese Argumentation ist falsch. Der Leiter ist nicht positiv geladen. Er sieht nur aus der Perspektive der bewegten Ladung positiv geladen aus. Der Leiter ist relativ zur Bewegung des Elektrons positiv geladen.
Damit das Experiment tatsächlich funktioniert, benötigen Sie aber eine ziemlich starke Batterie, denn mit dem Wechselstrom von der Steckdose funktioniert es natürlich nicht. Denn beim Wechselstrom fliessen die Elektronen ja nicht einheitlich in eine Richtung.
9. Längenkontraktion fotografiert
In manchen populärwissenschaftlichen Büchern wirt die Längenkontraktion illustriert, indem verschiedene Gegenstände verkürzt gezeichnet werden. Was würde man sehen, wenn man einen schnell bewegten Gegenstand fotografieren würde? Tatsächlich ist die Sache etwas komplizierter. Denn weil die Lichtgeschwindigkeit endlich ist, treten zusätzliche Effekte auf, die wir aus dem Alltag kennen, wenn wir z. B.einen Ball von einem fahrenden Zug werfen.
Betrachten wir statt Licht einen Schneeball. Sagen wir, ein Fussgänger ‘sieht’ den Schneeball, wenn er ihm gerade ins Gesicht fliegt. Er ‘sieht’ den Schneeball nicht, wenn der Schneeball ihn auf dem Hinterkopf oder von der Seite trifft. Nun betrachten wir einen Zug, der mit hoher Geschwindigkeit vZ am Fussgänger vorbeifährt. Auf der Rückseite des Zuges steht ein Bub, der einen Schneeball mit der Geschwindigkeit vS vom Zug wegschleudert. Im Ruhesystem, in dem der Fussgänger steht, addieren sich die Geschwindigkeiten vZ und vS zur Geschwindigkeit vF. Wenn der Fussgänger schaut, wie ihm der Zug entgegenkommt, so trifft ihn der Schneeball mit vF schräg von vorne, der Fussgänger kann den Schneeball also ‘sehen’, obwohl der Ball von der Rückseite des Zuges kommt.
Abbildung 9a) Ein Zug fährt mit der Geschwindigkeit a an einem Fussgänger vorbei. Ein Bub steht hinten auf dem Zug und wirft einen Schneeball mit Geschwindigkeit vS zur Seite.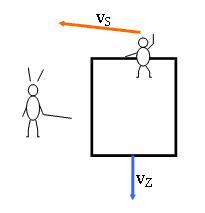
b) Die Geschwindigkeiten a und b addieren sich. Der Schneeball fliegt mit der Geschwindigkeit vS+vZ=vF dem Fussgänger entgegen. Obwohl der Ball von der Rückseite des Zuges weggeworfen wird, fliegt er dem Fussgänger ins Gesicht.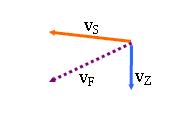
c) Was der Fussgänger tatsächlich sehen und fotografieren würde. Details siehe (Sex 2).
In der Relativitätstheorie ändert sich diese Überlegung leicht, weil zusätzlich zum beschriebenen Effekt, die Länge des Wagens verkürzt erscheint. Dies hat zur Folge, dass der Wagen genauso aussieht, wie wenn er gedreht wäre (Sex 2).
10. E = mc2
Die Formel E=mc2, eine der berühmtesten Formeln der Physik, stammt auch aus der speziellen Relativitätstheorie. Sie herzuleiten ist ein bisschen schwieriger als die obige Formel für die Zeitdilatation. Es ist aber nicht so schwierig, zu verstehen, was die Formel bedeutet.
Auf der linken Seite der Formel steht E, die Energie, auf der rechten steht eine Masse multipliziert mit der Lichtgeschwindigkeit im Quadrat. Die Formel zeigt also einen Zusammenhang zwischen einer Masse und einer Energie. Zu jeder Masse gehört eine Energie und zu jeder Energie gehört ein Gravitationsfeld.
In der Praxis sieht das z. B. so aus: Um zwei miteinander verbundene Teilchen zu trennen, muss Energie aufgewendet werden. Wenn sich umgekehrt zwei Teilchen verbinden, wird Energie frei. Zwei Teilchen, die miteinander verbunden sind, haben also weniger Energie als dieselben Teilchen, wenn sie nicht verbunden sind. Die Formel sagt, dass die verbundenen Teilchen leichter sind, als die nicht verbundenen.
Zum Beispiel kann sich ein Proton und ein Neutron zu einem Deuteron verbinden. Das Deuteron ist aber leichter, als ein Proton plus ein Neutron (siehe die folgende Aufstellung).
Ein Proton wiegt 1,6726485 · 10-27 kg
Ein Neutron wiegt 1,6749543 · 10-27 kg
Summe: 3,3476028 · 10-27 kg
Vergleich mit Deuteron: 3,3436377 · 10-27 kg
Das Deuteron ist 0.0039651 · 10-27 kg zu leicht! Wo geht die Masse hin, wenn zwei Teilchen verbunden werden?
Um ein Deuteron aufzuspalten braucht es Energie, es muss also Energie zu den Teilchen hinzugefügt werden, um sie zu trennen. Dann wird aber auch Masse hinzugefügt, die Teilchen werden also schwerer. Werden ein Proton und ein Neutron zusammengefügt, wird diese sogenannte Bindungsenergie frei, indem ein Photon (also Licht) abgestrahlt wird.
Wenn wir ein Neutron und ein Proton gegen ein Deuteron auf die Wage legen, so steigt die Schüssel mit dem Deuteron drin nach oben, während die fehlende Masse als Lichtteilchen entschwindet.
Abbildung 10 Ein Deuteron (rechts gestrichelt) besteht aus einem Proton (schwarz) und einem Neutron (grau). Das Deuteron wiegt aber weniger als ein Proton und ein Neutron, die nicht verbunden sind. Wenn ein Proton und ein Neutron verbunden werden, entweicht Energie, also Masse, in Form von Licht. Dies ist durch den Blitz rechts dargestellt.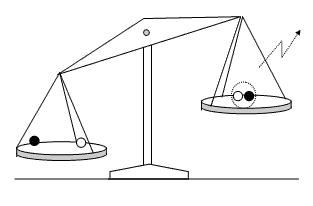
Bemerkenswert ist, dass in der Formel E=mc2 die Lichtgeschwindigkeit im Quadrat vorkommt. Die Lichtgeschwindigkeit ist eine enorm grosse Zahl und c2 bedeutet, dass eine sehr kleine Masse eine riesige Energie enthält. Zum Beispiel wurde bei der Atombombe von Hiroschima nur gerade ein Gramm Masse in Energie umgewandelt.
11. Das Minkowski-Diagramm
Viele der obigen Phänomene lassen sich mit dem sogenannten Minkowski-Diagramm sehr praktisch darstellen. Insbesondere die Zeitdilatation, die Längenkontraktion und die Frage, wie es mit der Kausalität in der speziellen Relativitätstheorie steht. Da das Minkowski-Diagramm bei Wikipedia bereits sehr klar erklärt wird, beschränke ich mich hier auf eine Kurzversion.
Wie wir gesehen haben, sind nach der speziellen Relativitätstheorie Zeit- und Längenangaben nur relativ zu einem Inertialsystem möglich. Eine wichtige Aufgabe der speziellen Relativitätstheorie ist deshalb, Längen- und Zeitangaben von einem Inertialsystem in ein anderes umzurechnen. Im Minkowski-Diagramm sind nun zwei Raum-Zeit-Diagramme, nämlich für jeden Beobachter eines, überlagert. So kann man aus den Zeit- und Ortsangaben des einen Beobachters problemlos die des anderen ablesen (Abbildung 11).
Abbildung 11 Das Minkowski-Diagramm
Im Minkowski-Diagramm wird jeweils nur eine Raumdimension gezeichnet. Das System (ct’, x’) bewegt sich mit konstanter Geschwindigkeit relativ zum System (ct, x). Auf der x-, und der x’-Achse sind die Abstände in Lichtsekunden eingezeichnet. Auf der ct- und der ct’-Achse die Zeiten in Sekunden. So ist ist beiden Systemen der Weg des Lichts gerade die Winkelhalbierende zwischen den Achsen (orange gepunktete Gerade).
Wenn die Winkelhalbierende der ct-Achse und der ct’-Achse gerade die Senkrechte ist (wie in der Zeichnung), dann sind die Massstäbe auf beiden Achsen gleich. Das Gleiche gilt für die x- und die x’-Achse.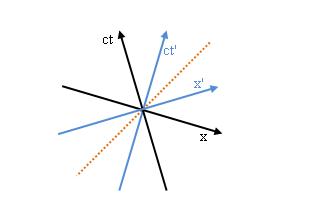
Die Ereignisse, die im blauen System (ct’, x’) gleichzeitig sind, liegen auf Parallelen zur x’-Achse (Abbildung 12a). Die Ereignisse, die im blauen System (ct’, x’) am gleichen Ort stattfinden, liegen auf Parallelen zur ct’-Achse (Abbildung 12b).
Abbildung 12a Gleichzeitige Ereignisse im System (ct’, x’) liegen auf Parallelen zur x’-Achse.
Abbildung 12b Ereignisse, die im System (ct’, x’) am gleichen Ort stattfinden, liegen auf Parallelen zur ct’-Achse.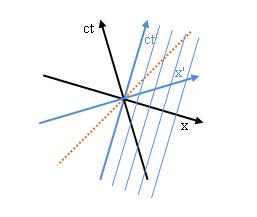
Ein Beobachter, der im System (ct’, x’) ruht, hat eine Weltlinie, die parallel zur ct’-Achse liegt. Er bewegt sich im System (ct, x), denn hier schneidet er die Parallelen zur ct-Achse (Abbildung 13).
Abbildung 13 Ein im System (ct’, x’) ruhender Beobachter bewegt sich im System (ct, x). Im Diagramm sieht man dies daran, dass seine Weltlinie (gestrichelte, blaue Linie) die Parallelen zur Achse ct schneidet.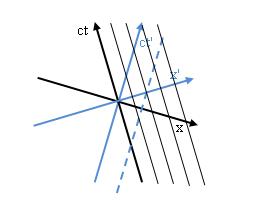
12. Überlichtgeschwindigkeit und Zeitreisen
Nach der speziellen Relativitätstheorie kann sich kein Teilchen, keine Energie und keine Information schneller als mit Lichtgeschwindigkeit ausbreiten oder bewegen. In den Minkowski-Diagrammen in Abbildung 14 sind wieder die Weltlinien des Lichts eingezeichnet. Diese sind immer die Winkelhalbierenden zwischen den Orts- und Zeitachsen, liegen also im Winkel von 45° zur Waagrechten. Da sich alle Gegenstände langsamer als mit Lichtgeschwindigkeit bewegen, können die Weltlinien von realen Dingen nie flacher werden als 45°. Diese Weltlinien des Lichts sind deshalb so wichtig, weil sie zeigen, ob zwei Ereignisse sich gegenseitig beeinflussen können.
Ein Ereignis im Ursprung des Koordinatensystems kann Auswirkungen haben auf Ereignisse innerhalb des oberen Lichtkegels (Abbildung 14a). Und es kann nur beeinflusst worden sein von Ereignissen innerhalb des unteren Lichtkegels. Wenn ein Ereignis ein anderes beeinflussen kann, so nennen wir ihren Abstand in der Raumzeit zeitartig. In diesem Fall gibt es ein Inertialsystem, in dem die beiden Ereignisse am gleichen Ort stattfinden. Ein Beobachter an diesem Ort muss dann nur die Zeit abwarten, bis das zweite Ereignis eintritt.
Wenn ein Ereignis das andere nur durch ein Signal mit Lichtgeschwindigkeit beeinflussen kann, so sagen wir, der Abstand zwischen den Ereignissen ist lichtartig.
Wenn zwei Ereignisse sich gegenseitig nicht beeinflussen können, so nennen wir den Abstand zwischen den zwei Ereignissen raumartig (Abbildung 14b). Zu solchen Ereignissen gibt es ein Inertialsystem, in dem die zwei Ereignisse gleichzeitig, aber an verschiedenen Orten stattfinden.
Abbildung 14a Ein Ereignis im Ursprung des Koordinatensystem kann nur Ereignisse im oberen Lichtkegel beeinflussen. Der Abstand vom Koordinatenursprung zu einem beliebigen Ereignis im oberen oder im unteren Lichtkegel ist zeitartig.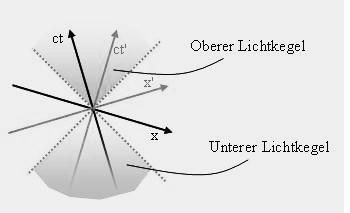
Abbildung 14b Wenn ein Ereignis nicht durch ein Ereignis im Ursprung beeinflusst werden kann und auch nicht auf dieses einwirkt, so gibt es ein Inertialsystem, in dem die zwei Ereignisse gleichzeitig, aber an unterschiedlichen Orten stattfinden.
Ob der Abstand zwischen zwei Ereignissen raumartig, zeitartig oder lichtartig ist, ist für alle Beobachter gleich. Das ist ganz wichtig. Denn wäre es anders, so wäre die kausale Struktur der Welt nicht für alle Beobachter gleich. Wenn ein Täter A durch irgendeine Rakete oder ein Signal ein Opfer B tötet, so ist A in jedem Inertialsystem der Mörder von B.
Was würde es bedeuten, wenn zwei Hexen Signale mit Überlichtgeschwindigkeit aussenden könnten? Sexl und Schmidt (Sex 2) machen dazu ein schönes Beispiel (Abbildung 15). Die Hexe Alice schaut sich die Lottozahlen von heute an. Sie sendet diese mittels Hyperradiowellen (rot-schwarz), also mit Überlichtgeschwindigkeit zu ihrer Hexenkollegin Betty, die gerade mit einem Besen mit sehr hoher Geschwindigkeit vorbei fliegt (Bettys Weltlinie). In Alices Inertialsystem vergeht dabei eine positive Zeit. In Bettys Inertialsystem aber kommt Nachricht an, bevor sie abgeschickt wurde. Betty sendet sogleich die Lottozahlen zurück zu Alice. Auch aus Sicht von Betty vergeht eine positive Zeit, nämlich Dt’. In Alices System kommt die Nachricht aber an, bevor sie abgeschickt wurde. Alice kann nun noch vor dem Einzahlungsschluss ihren Lottozettel abgeben.
Wir schliessen daraus, dass sich nichts mit Überlichtgeschwindigkeit bewegen oder ausbreiten kann. Allerdings gilt die Argumentation nur für die Zwei-Weg-Lichtgeschwindigkeit von A zu B und wieder zu A zurück. Es wäre mit Einsteins Formeln vereinbar, wenn eine Botschaft von A nach B mit Überlichtgeschwindigkeit gesendet würde, wenn dafür die Geschwindigkeit von B zu A entsprechend kleiner wäre. Dies ist nach der Lorentzianischen Interpretation der Relativitätstheorie der Fall (Sel 2).
Abbildung 15 Alice ist im Inertialsystem (ct, x) in Ruhe. Betty sitzt im Inertialsystem (ct’, x’) und fliegt in einiger Entfernung sehr schnell an Alice vorbei. Alice sendet mit Überlichtgeschwindigkeit (Hyperradiowellen) eine Botschaft an Betty. Diese sendet die Botschaft sogleich ebenfalls mit Überlichtgeschwindigkeit an Alice zurück. Dann würde Alice die Botschaft erhalten, bevor sie sie abschickt.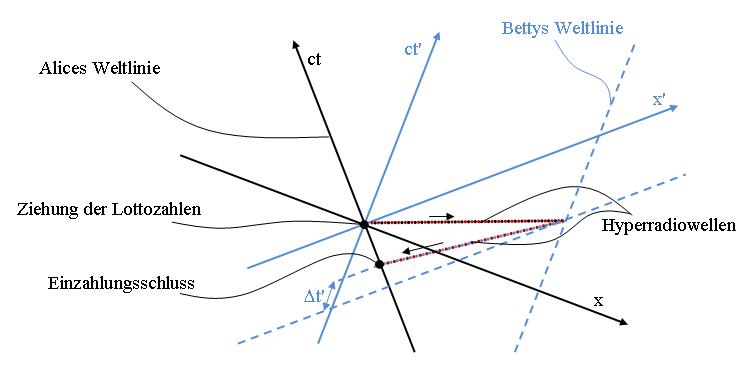
13. Weiterführende Literatur
Artikel auf dieser Homepage:
Überlichtgeschwindigkeit
Das Zwillingsparadoxon
Effekte der allgemeinen Relativitätstheorie
Gravitation
Externe Links:
Minkowski-Diagramm (wikipedia)
Film einer relativistischen Fahrt durch Tübingen
Didaktisches Material und Animationen zur Relativitätstheorie
Weiterführende Bücher:
Brandes Jürgen, ‘Die relativistischen Paradoxien und Thesen zu Raum und Zeit – Interpretationen der speziellen und allgemeinen Relativitätstheorie’, (1995), Verlag relativistischer Interpretationen – VRI, Karlsbad
Eine wunderschöne Zusammenstellung aller Fragen, welche die Relativitätstheorie verwirrend machen. Z. B.: Garagenproblem, Woodsches Paradoxon, Deckelparadoxie, Ehrenfes-Paradoxie, Zwillingsparadoxon.
Brandes Lösung: Das Problem durchrechnen und feststellen, dass nichts paradox ist.
Einstein Albert, ‘Über die spezielle und die allgemeine Relativitätstheorie, gemeinverständlich’, Springer, (1916)
Nach wie vor eine der besten Einführungen in die Relativitätstheorie, das Werk von ihrem Schöpfer selbst.
Selleri / Brandes et a., (1998) ‘Die Einsteinsche und Lorentzianische Interpretation der speziellen und allgemeinen Relativitätstheorie’, Verlag relativistischer Interpretationen – VRI, Karlsbad
Als Einstein die Relativitätstheorie schuf, ging er bewusst der Einfachheit halber davon aus, der Weg von A nach B sei gleich lang wie der Weg von B nach A. Nur mit dieser Annahme ist das Relativitätsprinzip erfüllt. Die Autoren zeigen, dass auch andere Lösungen möglich wären, und dass diese Lösungen möglicherweise philosophisch interessante Implikationen hätten. Alle Formeln und Voraussagen aus Einsteins Theorie bleiben aber gültig. Es geht also nicht darum, die Relativitätstheorie zu widerlegen, sondern einen anderen Blickwinkel aufzuzeigen.
Gemäss einer persönlichen Mitteilung von Jürgen Brandes wird in der neuesten Ausgabe ein Beispiel vorgerechnet, mit dem ein experimenteller Entscheid zwischen den beiden Interpretationen möglich ist.
Sexl / Raab / Streeruwitz, ‘Materie in Raum und Zeit – Eine Einführung in die Physik, Band 3’, (1980), Sauerländer
Wie alle Bücher von Sexl didaktisch hervorragend und sehr sorgfältig geschrieben. Eine erste Einführung in die moderne Physik auf Abitur- bzw. Maturitätsniveau. Weniger ausführlich als Sex 2, dafür enthält es auch noch andere Bereiche der modernen Physik auf sehr elementarem Niveau.
Sexl Roman, Schmidt Herbert K., ‘Raum-Zeit-Relativität’, (1989), Vieweg Studium, Braunschweig
Wie alle Bücher von Sexl didaktisch hervorragend und sehr sorgfältig geschrieben. Eine erste Einführung in die moderne Physik auf Abitur- bzw. Maturitätsniveau. Etwas ausführlicher als Sex 1.