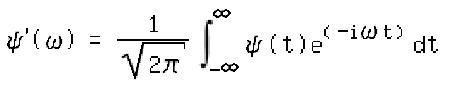Die Unbestimmtheitsrelation

Visits: 1385

Philipp Wehrli, 3. Juli 2006, erweitert um den Abschnitt zur Farbstoffchemie 26. Sept. 2011

In der klassischen Physik nimmt man an, dass Teilchen in der Realität unabhängig von der Messung gewisse eindeutig bestimmte Eigenschaften besitzen, z. B. einen Aufenthaltsort, eine Geschwindigkeit oder einen Drehimpuls. Werner Heisenbergs Unbestimmtheitsrelation (auch Unschärferelation genannt) besagt dagegen, dass diese Eigenschaften durch die Messanordnung überhaupt erst definiert werden und vorher nur als Möglichkeiten angelegt sind. Z. B. ist es nicht möglich, den Aufenthaltsort und den Impuls eines Teilchens gleichzeitig exakt zu kennen, weil die Begriffe Impuls des Teilchens A und Aufenthaltsort des Teilchens A nicht gleichzeitig eine Bedeutung haben.

Werner Heisenbergs Unbestimmtheitsrelation beruht auf einem Wellenphänomen, das auch bei klassischen Wellen bekannt ist: Es ist nicht möglich, bei einer Welle die Ankunftszeit und die Frequenz gleichzeitig exakt zu bestimmen, weil diese nicht gleichzeitig definiert sind. Es ist nicht schwierig, z. B. bei einer Wasserwelle die Frequenz zu bestimmen. Ich setze mich einfach auf einen Schiffssteg, zähle eine Minute lang die Wellenbuckel, die vorüberziehen, und berechne daraus die Frequenz. Was aber ist die Ankunftszeit dieser Welle?

Ich habe eine Minute lang Wellenbuckel gezählt, kann also die Ankunftszeit nur auf eine Minute genau angeben. Vielleicht hätte ich nicht eine Minute lang zählen müssen. Aber wenn ich die Frequenz einigermassen exakt bestimmen will, so muss ich zumindest die Zeit zwischen zwei Wellenbuckeln messen.

Könnte ich die Ankunftszeit noch weiter verkürzen?

Ich könnte einen Teil der Welle herausschneiden, indem ich z. B. eine Schleuse ganz kurz öffne und gleich wieder schliesse. Hinter der Schleuse hätte ich dann ein ganz kurzes Wellenpaket, das wie ein Knall zu einem präzise definierten Zeitpunkt bei mir ankommt. Wie unten näher ausgeführt, besitzt aber so ein Wellenpaket keine eindeutige Frequenz, sondern es ist eine Überlagerung von Wellen verschiedener Frequenzen.

Wenn ich also die Frequenz einigermassen exakt bestimme, dauert die Ankunft etwa so lange, bis zwei Wellenbuckel am Ziel sind. Die Ankunftszeit ist nicht genauer definiert. Mathematisch ergibt sich die Formel:

(1) Δν·ΔT > 1/2π

Wobei ΔT die Unbestimmtheit der Ankunftszeit ist und Dn die Unbestimmtheit der Frequenz, also der Unterschied zwischen der kleinsten und der grössten Frequenz, die möglich sind.

Nach Einstein besteht Licht aus Wellenpaketen (Photonen), deren Energie E proportional zur Frequenz ν der Welle ist (h ist das Plancksche Wirkungsquantum):

(2) E = hν

Wenn die Frequenz der Welle unbestimmt ist, dann ist also auch die Energie unbestimmt. Für Quanten ergibt sich die folgende Unbestimmtheitsrelation:

(3) ΔE·ΔT > 1/2π

Das heisst: Wenn ich die Energie E eines Teilchens sehr genau bestimmen will, dann kann ich fast nicht über die Ankunftszeit des Teilchens im Messapparat aussagen. Wenn ich umgekehrt genau messe, wann ein Teilchen im Messapparat ankommt, weiss ich nichts über seine Energie.

Hinweis für Profis: Im Formalismus der Quantenmechanik wird die Unbestimmtheit von Energie und Zeit nur indirekt hergeleitet, weil es keinen Operator für die Zeit gibt. Man muss sich also im konkreten Fall sehr genau überlegen, was ΔT bedeutet.

1. Bemerkung: Die Heisenbergsche Unbestimmtheit liegt nicht daran, dass ich ungeschickt messe. Es ist auch nicht so, dass die Messung die Welle ‚stört’ oder ‚verändert’, wie man oft liest. Experimente wie die unter Quantenradierer und komplementäre Grössen dargestellten wären nicht möglich, wenn die Quantenwellen so leicht gestört würden.
2. Bemerkung: Der Unterschied zwischen den klassischen Wellen und den Quantenwellen liegt in der Formel (2). Wenn ich bei einer Wasserwelle ein Stück herausschneide, z. B. indem ich eine Schleuse kurz öffne und gleich wieder schliesse, dann geht ein Teil der Energie durch die Schleuse hindurch, während ein anderer zurückgeworfen wird. Bei einem Photon wird die Energie nie gespalten. Immer geht entweder die gesamte Energie hindurch oder die gesamte Energie wird reflektiert. Das Seltsame der Quantentheorie ist also nicht die Unbestimmtheit, sondern die Tatsache, dass Quanten einerseits wie Wellen Interferenzmuster zeigen und insofern eine Ausdehnung haben, aber andererseits immer nur an einem Punkt dieser Welle tatsächlich gemessen werden.

Was geschieht in einem Experiment, in dem ich die Frequenz messe?

Um zu verstehen, dass sich die Unbestimmtheitsrelation nicht umgehen lässt, lohnt es sich, einige Experimente anzuschauen. Angenommen, ich will die Frequenz eines Lichtimpulses messen, also eines kleinen Wellenpakets. Wie kann ich dies tun? Die Frequenz von Licht ist so hoch, dass ich nicht zuschauen und zählen kann, wie schnell die Wellenbuckel ankommen. Weil die Lichtgeschwindigkeit c aber konstant ist, hängt die Frequenz aber direkt mit der Wellenlänge l des Lichtes zusammen, nämlich so:

(4) ν = c/λ

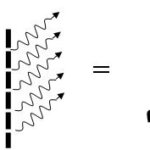
Ich kann also statt der Frequenz die Wellenlänge messen und damit die Frequenz berechnen. Die Wellenlänge von Licht messe ich mit einem optischen Gitter. Angenommen, ein Wellenpaket trifft auf ein optisches Gitter mit vielen engen Spalten. Ist der Gangunterschied zweier Strahlen ein Vielfaches der Wellenlänge, so überlagern sich die Wellenbuckel mit Wellenbuckeln. Dabei wird der Wellenzug aber verlängert, so dass die Ankunftszeit nur noch sehr unpräzise definiert ist (Abbildung 1).

Abbildung 1

Ein Wellenpaket trifft auf ein optisches Gitter.

In einer bestimmten Richtung überlagern sich die Wellen einer bestimmten Frequenz.

Dabei wird aber der Wellenzug viel länger. Die Wellenlänge und die Frequenz sind jetzt bestimmt, aber die Ankunftszeit ist nicht mehr definiert.

Hinter dem Gitter ist nicht eruierbar, ob das Licht durch die oberste oder die unterste Spalte kam. Der Wellenzug wird deshalb viel länger. Dieser Versuch funktioniert auch mit einzelnen Photonen, also mit Lichtteilchen, die immer genau an einem Ort ankommen.

Die Fouriertransformation

Wenn ich also einen kurzen Wellenzug habe und dessen Frequenz bestimmen will, dann verlängert sich der Wellenzug. Was geschieht, wenn bei einem langen Wellenzug mit bestimmter Frequenz ein Stück herausschneide, um dessen Ankunftszeit zu messen?

Der Mathematiker Joseph Baron de Fourier bewies, dass jedes Wellenpaket als Überlagerung von Wellen verschiedener Frequenzen eindeutig beschrieben werden kann. Jedes Wellenpaket kann also auf zwei verschiedene Arten eindeutig beschrieben werden.

1. Ich kann angeben, wie gross die Auslenkung zu einer bestimmten Zeit an einem bestimmten Ort ist.
2. Ich kann die Frequenzen der Sinus- und Cosinusschwingungen angeben, aus denen das Wellenpaket zusammengesetzt ist. (Normalerweise sind dazu unendlich viele solche ‚harmonische’ Wellen nötig).

Die so genannte Fouriertransformation zeigt, wie ich von der einen Darstellung in die andere umrechnen kann und umgekehrt.

1. Beispiel:

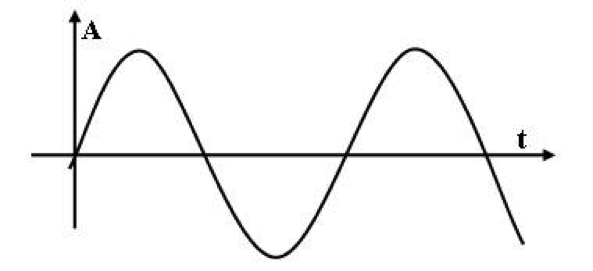
Die Welle sei in der 1. Darstellung eine Sinusschwingung (Abbildung 2).

Abbildung 2

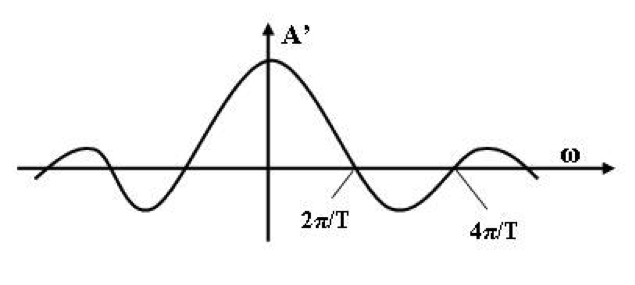
Die Sinusschwingung hat genau eine Frequenz. Also hat in der 2. Darstellung nur gerade eine Frequenz eine Intensität grösser als null (Abbildung 3):

Abbildung 3

2. Beispiel:

Wir betrachten die oben beschriebene Wasserwelle. Eine Schleuse wurde kurz geöffnet und gleich wieder geschlossen. Durch die Schleuse kommt eine Welle mit rechteckigem Querschnitt, also nach der 1. Darstellung (Abbildung 4):

Abbildung 4

Mit der Fouriertransformation kann man berechnen, welche Frequenzen in diesem Wellenpaket vorkommen und welche Intensität diese Wellen haben. Man erhält als 2. Darstellung (Abbildung 5):

Abbildung 5

Das heisst: Im obigen Wellenpakets befindet sich ein Spektrum unendlich vieler verschiedener Frequenzen. Die negativen Frequenzen kommen daher, dass in der Frequenz ω auch gleichzeitig die Phase angegeben ist, also die Information, wo die Sinusschwingung ihren Nullpunkt hat.

In der zweiten Darstellung finden wir in der Grafik das T unter dem Bruchstrich. Das heisst: Wenn wir in den Wellenzug in der ersten Darstellung kürzer machen, also die Schleuse nur sehr kurz öffnen, wird die Frequenz verschwommener. Genau dies ist die Aussage der Heisenbergschen Unbestimmtheitsrelation.

Ein Experiment, in dem ich die Ankunftszeit messe

Die Fouriertransformation ist abstrakt und vielleicht fragen Sie sich, ob Lichtwellen, also Photonen sich tatsächlich daran halten?

Tatsächlich haben Hauser und andere diesen Effekt in einem schönen Experiment nachgewiesen (Hau 1). Sie ‚zerhackten’ einen Laserstrahl mit den Speichen eines sehr schnell rotierenden Rades in kleine Wellenpakete. Danach massen sie die Frequenzen der Wellenpakete und stellten fest, dass die Photonen nun nicht mehr die Frequenz des Lasers hatten, sondern eine so genannte Linienverbreiterung zeigten, genau wie dies die Fouriertransformation und Heisenbergs Unbestimmtheitsrelation vorhersagte.

Welche Energie, also welche Farbe ein Photon hat, ist nicht alleine durch die Emission bestimmt, sie hängt sehr stark auch von den Bedingungen bei der Absorbtion ab.

Ist die Welt wellenartig?

Die Fouriertransformation zeigt noch etwas anderes. Im 2. Beispiel müssen wir es gar nicht mit einer Welle zu tun haben. Im Grunde genommen zeigt Abbildung 4. eine beliebige Messung, bei dem der Messwert nicht absolut exakt bestimmt wurde. Der Messwert liegt zwischen –T/2 und +T/2. Mit der Fouriertransformation wird diese Situation in eine Wellenschreibweise übertragen. Der Messwert, der vorher nichts mit Wellen zu tun hatte, wird plötzlich als Überlagerung von Wellen mit verschiedenen Frequenzen beschrieben. Wir können uns fragen, ob die Welt tatsächlich wellenartig ist oder ob die Wellen nur durch unsere Beschreibung oder durch die Art der Messinstrumente auftauchen.

Andere Unbestimmtheitsrelationen

Nach dem obigen erstaunt es nicht, dass es noch weitere Unbestimmtheitsrelationen gibt. In der Tat ist in der Quantentheorie eine ganze Reihe von Paaren von Messgrössen bekannt, die nicht gleichzeitig gemessen werden können, z. B.:

Impuls – Ort
Drehimpuls – Winkel
Energie – Zeit
Phase – Photonenzahl

Die Fouriertransformation mathematisch

Mit der folgenden Formel kann das Frequenzspektrum einer aperiodischen Funktion Y(t) berechnet werden:

Umgekehrt kann aus einem Frequenzspektrum ψ´(ω) die zu Grunde liegende Funktion ψ(t) berechnet werden:

ψ(t) ist die Fourier-Transformierte von ψ´(ω), ψ´(ω) die inverse Fourier-Transformierte von ψ(t).

Anwendungen in der Farbstoffchemie

Zur Unbestimmtheitsrelation gibt es eine ganze Reihe von Anwendungen. Für Leser, die einen kleinen Rechenaufwand nicht scheuen, will ich ein Beispiel aus der Farbstoffchemie vorführen. Dieser Abschnitt ist eine Kurzfassung eines Artikels von Norbert Treitz in Spektrum der Wissenschaft Nov. 2010.

In der Farbstoffchemie gilt die empirische Regel, dass kurze Kohlenstoffketten eher kurzwelliges Licht absorbieren, während längere Ketten eher langwelliges Licht aufnehmen. Diese Regel ist eine Folge der Unbestimmtheitsrelation, wie die folgende Überlegung zeigt.

In den Lehrbüchern werden zwischen den Kohlenstoffatomen dieser Ketten meist alternierend Einfach- und Doppelbindungen gezeichnet. Tatsächlich haben die Atomkerne aber oft alle den gleichen Abstand von L=0,14nm. Wo die Einfach- oder Doppelbindungen gerade sind, ist unbestimmt. Man könnte sich vorstellen, von jedem Kohlestoffatom fliege je ein Elektron frei zwischen den Enden der Kette hin und her, nämlich ein Elektron von jeder Doppelbindung. Dieses Bild ist aber nicht ganz korrekt, weil es den Wellenaspekt der Elektronen nicht berücksichtigt. Vielmehr haben die Elektronen nach de Broglie eine Wellenlänge λ=h/π, wobei die λ/2 Teiler der Länge der Kohlenstoffkette sein muss.

Ausserdem dürfen nach dem Pauli Prinzip höchstens zwei Elektronen im gleichen Energiezustand sein, wobei sie aber entgegengesetzten Spin haben müssen. In einer Kette von 2N Kohlenstoffatomen gibt es also 2N freie Elektronen, die jeweils paarweise den gleichen Energiezustand besetzen. Das Paar im niedrigsten Energiezustand schwingt mit der Wellenlänge λ₁=4NL, denn die halbe Wellenlänge muss gerade die Länge der Kohlenstoffkette sein. Das Paar im zweitniedrigsten Zustand hat die Wellenlänge λ₂=4NL/2. Das N-te Paar hat die Wellenlänge λ_N=4NL/N=4L. Die Energie dieser Elektronen ist
E_N = h²/(2mλ_N²) = h²/(32L²m), wobei m die Masse des Elektrons ist, h das Plancksche Wirkungsquantum und L=0,14 der Abstand zwischen den Kohlestoffatomen der Kette. Für das energiereichste Paar spielt also die Länge der Kette keine Rolle.

Die Farbe eines Moleküls entsteht dadurch, dass ein Elektron Licht aufnimmt und dadurch auf ein höheres Energieniveau gehoben wird. Besonders häufig geschieht dies bei den Elektronen des höchsten Energieniveaus, also vom Niveau E_N=h²/(32L²m) zum Niveau
E_N+1 = h²/(2mλ_N+1²) = h²/(32L²mN²/(N+1)²) = E_N(N+1)²/N²
Der Energieunterschied E_N-E_N+1 beträgt:
ΔE_min = E_N+1-E_N = E_N((N+1)²-N²)/N² = E_N(2N+1)/N^{2
Für lange Ketten können wir 2N+1 ungefähr gleich 2N setzen, so dass}
ΔE_min = 2E_N/N = h²/(N16L²m)
Die Wellenlänge des dazugehörenden Lichts ist
λ=16mNL²c/h
Diese Wellenlänge ist für lange Kohlenstoffketten proportional zur Anzahl N der Kohlenstoffatome in der Kette.

Weiterführende Artikel auf dieser Homepage:

Sind Teilchen, die niemand beobachtet, real?
Einstein-Podolsky-Rosen Experiment
Quantenradierer

Weiterführende Bücher:

Philip Wehrli, ‘Das Universum, das Ich und der liebe Gott’, (2017), Nibe Verlag,

In diesem Buch präsentiere ich einen Gesamtüberblick über mein Weltbild: Wie ist das Universum entstanden? Wie ist das Leben auf der Erde entstanden? Was ist Bewusstsein und woher kommt es? Braucht es dazu einen Gott?
Viele Artikel dieses Blogs werden in diesem Buch in einen einheitlichen Rahmen gebracht, so dass sich ein (ziemlich) vollständiges Weltbild ergibt.

Leserunde bei Lovelybooks zum Buch ‘Das Universum, das Ich und der liebe Gott’, von Philipp Wehrli (abgeschlossen)

Rezensionen bei Lovelybooks
Rezensionen bei Amazon
Film-Präsentation zum Buch
Nibe Verlag

 

Feynman / Leighton / Sands, ‘Feynman Vorlesungen über Physik, Band III: Quantenmechanik’, (1988), Ouldenbourg, München / Wien
Wer Physik studiert, kennt und schätzt Feynman. Sehr ausführlich, aber auch sehr originell und didaktisch geschickt erklärt der Nobelpreisträger die Quantenmechanik. Das Buch ist das Vorlesungsskript für die Grundvorlesung und setzt demgemäss ein wenig Mathematik voraus. Feynman zeigt, wie man mit Spins rechnet und rechnet das obige Beispiel vor.

Paul Harry, ‘Photonen- Eine Einführung in die Quantenoptik’, (1999), Teubner Studienbücher, Leipzig
Etwas vom Besten, was zur Quantentheorie geschrieben wurde! Paul stellt die schönsten Experimente der Quantenoptik vor und analysiert scharfsinnig, weshalb die klassische Physik versagen muss. Die ideale Einführung für alle, die nicht nur rechnen, sondern die Natur auch verstehen wollen. Benützt nur sehr einfache Mathematik.

Spektrum Akademischer Verlag, Heidelberg, ‘Quantenphilosophie – Reihe Verständliche Forschung’, Neuser / Neuser-von Oettingen (Herausgegeber)
Wer sich für die Philosophie hinter der Quantentheorie interessiert, findet hier ein breites Spektrum anregender Artikel, unter anderem von Schrödinger, Gamov, d´Espagnat, Cassidy und de Witt. Die Artikel sind kurz, prägnant und allgemeinverständlich und werden mit vielen schönen Grafiken illustriert.

Zeilinger Anton, ‘Einsteins Spuk – Teleportation und weitere Mysterien der Quantenphysik’
Eine auch für Nicht-Wissenschafter nachvollzierbare, lebendig geschriebene Schilderung der EPR Experimente und der Quantenteleportation von dem Physiker, der die Experimente selber durchgeführt hat.