Visits: 1913
Philipp Wehrli, 12. März 2006, ergänzt am 26. Dezember 2013 um den Abschnitt Bedeutung.
Bayes Erkenntnisformel ist für die Erkenntnistheorie das, was Darwins Evolutionstheorie für die Biologie ist. Thomas Bayes zeigte, wie aus fast vollständiger Unwissenheit Schritt für Schritt Erkenntnis wachsen kann, so wie Darwin erklärte, wie sich aus fast unbelebter Materie Schritt für Schritt hochkomplexe Lebewesen entwickeln können. Wir müssen weder an Kants apriori Wissen glauben, noch an Platons eidos, die mystischen Ideen, noch an göttliche Eingebung. Es besteht Hoffnung, dass sich die Evolution des Wissens nahtlos in die Evolution des Lebens und des Bewusstseins einfügt.
1. Wahrscheinlichkeit
Die Wahrscheinlichkeitsrechnung, welche wir in der Schule gelernt haben, ist für den Alltag und für die Naturwissenschaften nur sehr bedingt brauchbar. Sie geht von einer bekannten Welt aus und gibt dann Prognosen über zukünftige Ereignisse ab. Wir wissen z. B., wie viele Seiten ein Würfel hat und berechnen damit die Wahrscheinlichkeiten für verschiedene Würfe. Normalerweise sind wir aber in der umgekehrten Situation: Wir kennen einige Ereignisse und möchten wissen, wie die Wirklichkeit dahinter aussieht. Mehrere Mathematiker und Physiker haben mir versichert, eine solche Schlussfolgerung sei gar nicht möglich, bis mich schliesslich Prof. Huber von der Uni Zürich auf Bayes Statistik aufmerksam machte.
Die Wahrscheinlichkeit P ist definiert als die Anzahl Treffer dividiert durch die Anzahl aller Möglichkeiten:
P = (Anzahl Treffer) : (Anzahl Möglichkeiten)
Wenn ich z. B. einen Würfel habe, so sind die sechs Würfelseiten die sechs möglichen Resultate. Wenn ich nach der Wahrscheinlichkeit frage, dass entweder 1 oder 2 kommt, so sind 1 und 2 die zwei Treffer. Die Wahrscheinlichkeit, dass beim Wurf mit einem Würfel 1 oder 2 fällt, ist also:
P1 oder 2 = 2 : 6 = 1/3
Die entscheidende Annahme bei dieser Definition ist, dass beim häufigen Werfen jede der sechs Würfelseiten gleich häufig auftritt.
2. Bedingte Wahrscheinlichkeit
Nun hätte ich zum Würfeln auch ein Dodekaeder mit Zahlen drauf nehmen können. Ein Dodekaeder hat 12 fünfeckige Seiten. Die Wahrscheinlichkeit wäre dann
P(1 oder 2|Dod.) = 2 : 12 = 1/6
Hier habe ich eine neue Schreibweise eingeführt. Der senkrechte Strich | kennzeichnet eine bedingte Wahrscheinlichkeit. P(1 oder 2|Dod.) ist die Wahrscheinlichkeit dass 1 oder 2 kommt unter der Bedingung, dass ich ein Dodekaeder werfe. Das P(1 oder 2|Dod.) ist also von rechts nach links zu lesen: Das Dodekaeder ist schon ausgewählt und nun ist die Frage, mit welcher Wahrscheinlichkeit wir 1 oder 2 erwarten sollen.
In den obigen Beispielen wusste ich immer, wie die Welt aussieht, also wie viele Seiten der “Würfel” hatte. Ich könnte aber auch zuerst den Würfel auswählen, z. B. indem ich sie in Zeitung verpackt in einen Sack werfe, gut durchschüttle und dann blind eine Zeitung herausziehe. So wäre die Wahrscheinlichkeit, dass ich den Würfel erwische 1/2 und ebenfalls 1/2 für das Dodekaeder. In einen Wahrscheinlichkeitsbaum gezeichnet sieht die Sache so aus:
Abbildung 1 Wahrscheinlichkeitsbaum mit zwei Würfeln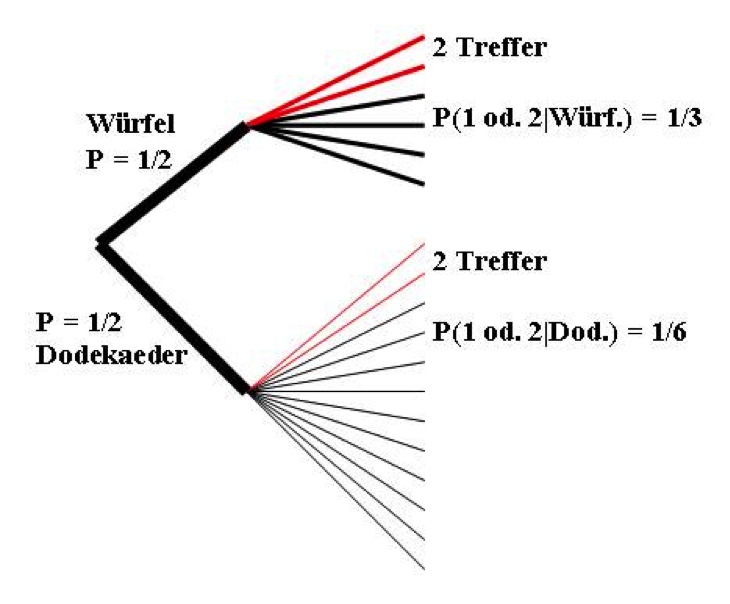
Es gibt also zwei Wege, 1 oder 2 zu erhalten. Erstens kann ich den Würfel erwischen und dann 1 oder 2 würfeln, oder ich kann das Dodekaeder ziehen und mit etwas mehr Glück zum gleichen Resultat kommen. Die Wahrscheinlichkeit, auf irgend einem Weg 1 oder 2 zu erhalten, beträgt:
P(1 oder 2) = P(1 oder 2|Würf.) · P(Würf.) + P(1 oder 2|Dod.) · P(Dod.)
Wenn ich den Versuch N mal durchführe, kann ich eine gewisse Anzahl Treffer erwarten, nämlich:
N · [P(1 oder 2|Würf.) · P(Würf.) + P(1 oder 2|Dod.) · P(Dod.)]
Die Anzahl Treffer, die mit dem normalen Würfel zustande kamen, ist:
N · P(1 oder 2|Würf.) · P(Würf.)
3. Bayes Erkenntnisformel für zwei Möglichkeiten
Nun haben wir alle Werkzeuge bereit, um Bayes Erkenntnisformel herzuleiten. Denken wir uns die folgende Situation:
Meine Freundin würfelt und ich weiss, dass sie dazu entweder einen normalen Würfel benutzt oder ein Dodekaeder. Sie nennt mir das Resultat und ich soll erraten, welchen “Würfel” sie geworfen hat. Natürlich findet meine Freundin es lustiger, das Dodekaeder zu werfen, aber dieses psychologische Vorwissen nützt mir nichts. Denn sie muss den geometrischen Körper in Zeitung verpackt aus einem Sack ziehen und erwischt in 50% der Fälle den normalen Würfel und in 50% das Dodekaeder.
Die Frage ist nun: Wenn meine Freundin 1 oder 2 gewürfelt hat, wie gross ist die Wahrscheinlichkeit P(Würf.| 1 oder 2), dass sie den normalen Würfel genommen hat? -Beachte, dass in P(Würf.| 1 oder 2) die Reihenfolge der Einträge vertauscht ist: Jetzt ist bekannt, dass 1 oder 2 gewürfelt wurde (deshalb ist “1 oder 2” rechts). Die Frage ist, ob der Würfel gewählt worden ist (deshalb ist “Würf.” links).
Wieder ist die Wahrscheinlichkeit P(Würf.| 1 oder 2) definiert als die Anzahl Treffer dividiert durch die Anzahl aller Möglichkeiten.
Die Anzahl Treffer sind nun gerade die obigen Anzahl Treffer, die mit dem normalen Würfel zustande kamen, also:
N · P(1 oder 2|Würf.) · P(Würf.)
Bei der Anzahl aller Möglichkeiten kommen noch die Treffer, die mit dem Dodekaeder erzielt wurden hinzu, also:
N · P(1 oder 2) = N · [P(1 oder 2|Würf.) · P(Würf.) + P(1 oder 2|Dod.) · P(Dod.)]
Damit wird Bayes Formel:
wobei das N weggekürzt werden kann.
Ich weiss also z. B., dass meine Freundin 1 oder 2 gewürfelt hat. Wie gross ist die Wahrscheinlichkeit, dass sie den normalen Würfel erwischt hat?
| P(Würf.) = ½ | (=a priori Wahrscheinlichkeit, dass sie den normalen Würfel zieht) |
| P(Dod.) = 1/2 | (= a priori Wahrscheinlichkeit, dass sie das Dodekaeder erwischt) |
| P(1 oder 2|Würf.) = 1/3 | (= Bedingte Wahrscheinlichkeit, dass 1 oder 2 kommt, falls der Würfel gezogen ist) |
| P(1 oder 2|Dod.) = 1/6 | (= Bedingte Wahrscheinlichkeit, dass 1 oder 2 kommt, falls das Dodekaeder gezogen ist) |
Damit wird Bayes Formel:
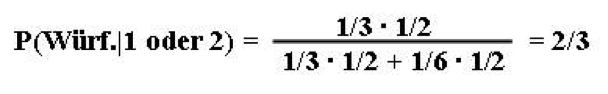
Bevor ich wusste, dass meine Freundin 1 oder 2 würfelte, betrug die Wahrscheinlichkeit, dass sie den normalen Würfel zog, 1/2. Aufgrund meines neuen Wissens muss diese Wahrscheinlichkeit auf 2/3 aktualisiert werden. (Man ist versucht zu sagen: “Die Wahrscheinlichkeit wird korrigiert.” ´korrigiert´ impliziert aber, dass die a priori Wahrscheinlichkeit falsch war. Sie war aber nicht falsch, sondern sie gab den damaligen Kenntnisstand korrekt wider.)
4. Beispiel mit mehreren Versuchen
Bei weiteren Würfen würde sich die Aussagekraft weiter verbessern. Angenommen, die Freundin zieht einmal ein Päcklein aus dem Sack (also entweder normalen Würfel oder Dodekaeder) würfelt dann mit dem gezogenen Ding 10 mal. Dabei erreicht sie immer eine Zahl zwischen 1 und 6. Wie gross ist die Wahrscheinlichkeit, dass sie den normalen Würfel benützt?
Wenn sie den normalen Würfel gezogen hat, so wird sie mit Sicherheit immer eine Zahl zwischen 1 und 6 würfeln, also Wahrscheinlichkeit 1. Wenn sie das Dodekaeder zieht, würfelt sie nur mit einer Wahrscheinlichkeit von
(1/2)10 zehnmal eine Zahl zwischen 1 und 6. Bayes Formel ergibt also:
Bereits nach zehn Würfen ist also das Resultat sehr eindeutig: Mit einer Wahrscheinlichkeit von 99.9% hat meine Freundin den normalen Würfel gezogen.
Bayes Formel mit mehr als zwei Würfeln
Analog kann Bayes Formel für mehr als zwei verschiedene Würfel aufgestellt werden:
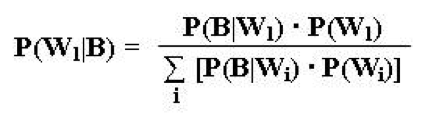
Dabei sind die Wi die verschiedenen Sorten von Würfeln, W1 ist der Würfel, der tatsächlich fällt und B ist das beobachtete Ereignis.
5. Kontinuierliche Werte
Selbstverständlich müssen die gemessenen Werte nicht diskret sein, wie bei den gewürfelten Zahlen. Z. B. könnte ein Motorenbauer sich fragen, welcher Anteil der produzierten Motoren fehlerhaft sind. Dazu nimmt er Stichproben und will anhand dieser Stichproben auf die Gesamtheit schliessen. Der Anteil der Ausschussproduktion soll in Prozent angegeben werden, also in einem kontinuierlichen Wert. Die Bayessche Statistik liefert dann eine Aussage der Form:
“Mit der Wahrscheinlichkeit p liegt die Ausschussproduktion bei diesem Verfahren zwischen x% und y%.”
Für die Details verweise ich auf das schöne Buch von Dieter Wickmann (Wic 1).
6. Geschätzte a priori Wahrscheinlichkeiten.
Wir haben zwar bereits einiges erreicht. Wenn wir die a priori Wahrscheinlichkeiten für die verschiedenen Würfel kennen, können wir nach den Würfen sehr gut abschätzen, mit welchem Würfel sie zu Stande kamen. In den Naturwissenschaften und im Alltag kennen wir aber normalerweise die a priori Wahrscheinlichkeiten nicht. In der Praxis müssen daher die a priori Wahrscheinlichkeiten meist geschätzt werden. Je nach Schätzung kommt man so auf unterschiedliche Resultate. Dies hat zu Kritik an Bayes Statistik geführt.
Beruhigenderweise fällt die Wahl der a priori Wahrscheinlichkeiten kaum je ins Gewicht. Je mehr Versuche durchgeführt werden, desto schneller nimmt die Bedeutung der a priori Wahrscheinlichkeiten ab. Selbstverständlich darf man die a priori Wahrscheinlichkeiten weder 0 noch 1 wählen. Oft setzt man sie für alle Möglichkeiten gleich, so wie ich dies im obigen Beispiel getan habe (beide Würfel werden mit gleicher Wahrscheinlichkeit gezogen). Es lohnt sich, ein bisschen mit den Zahlen zu spielen und z. B. in den obigen Beispielen die a priori Wahrscheinlichkeiten zu variieren.
7. Bedeutung
Meiner Ansicht nach wird Bayes Statistik vor allem in der Erkenntnistheorie massiv unterschätzt. Bayes Statistik ist die Grundlage aller Erkenntnis. Dies zeige ich im Artikel über das Induktionsprinzip. Unser Gehirn funktioniert grundsätzlich bayesianisch. Ich habe erst im Dezember 2013 erstaunt festgestellt, dass dies von manchen Gehirnforschern heute noch bezweifelt wird (siehe dazu den Artikel aus Gehirn & Geist, ‘Das bayesianische Gehirn’). In einem Leserbrief zu diesem Artikel schreibe ich:
“Ich bin überrascht, dass offenbar einige Fachleute bestreiten, dass das Gehirn bayesianisch denkt. Dies ist doch eine direkte Folge der Hebbschen Regel, nach der zwei Neurone A und B umso stärker miteinander verbunden werden, je häufiger sie gleichzeitig feuern.
Es sei P(A) die Häufigkeit, mit der A feuert, und P(B) die Häufigkeit, mit der B feuert. Weiter sei P(A|B) die Anzahl der Fälle, in denen A und B gleichzeitig feuern, dividiert durch die Zahl der Fälle, in denen B feuert. P(B|A) ist analog.
Dann ist die Anzahl N der Fälle, in denen A und B gleichzeitig feuern:
N = P(A|B) P(B) = P(B|A) P(A)
Dies ist gerade Bayes’ Formel!
Wenn wir berücksichtigen, dass Netze von Neuronen oft durch einzelne Neurone repräsentiert werden, ist klar, dass A und B auch für ganze Netze von Neuronen stehen können. Das Gehirn arbeitet also auf Basis von Bayes’ Formel.
Dabei ist die Verrechnung denkbar einfach. Es müssen nämlich keineswegs die einzelnen Zellen Bayes’ Formel beherrschen. Vielmehr spielt das Neuronennetzwerk als Parallelrechner sämtliche Möglichkeiten gleichzeitig durch. Zu den mir verfügbaren Daten sind in meinem Gehirn alle Interpretationsmöglichkeiten als Überlagerung repräsentiert. Von diesen wird die überzeugendste ausgewählt, d. h. diejenige, bei der die meisten Neuronen synchron feuern. Auch dies erfordert von den einzelnen Zellen keineswegs einen komplizierten Rechenvorgang. Die Zellen müssen nur zählen, wie oft sie gleichzeitig mit anderen Zellen feuern.”
In der Praxis sieht das dann etwa so aus: Ich hatte lange Zeit sehr schlechte Augen und hatte daher grosse Mühe, Menschen zu erkennen. Zwar fiel es mir leicht, in der Schule meine Mitschüler zu erkennen. Wenn ich die gleichen Schüler z. B. in einem Laden sah, erkannte ich sie oft nicht. Denn die Apriori Wahrscheinlichkeit, in der Schule einen Mitschüler zu treffen, ist hoch. In der Schule war also mein Gehirn darauf eingestellt, Mitschüler wahrzunehmen. Was wir sehen, hängt stark davon ab, was in den Kontext passt.
Lesen Sie bitte laut den Satz:
“Wir Erwachsenen können oft still vor uns hin weinen, aber beim Säugling bilden Schreien und Weinen eine untrennbare Einheit.” (Desmond Morris)
Ergänzen Sie nun die folgenden Buchstaben zu einem Wort:
Tr___e
Das Wort kann auf verschiedene Weise ergänzt werden. Es handelt sich um eine Aufgabe, die nicht mit exakter Logik gelöst werden kann. Im Alltag sind solche Aufgaben der Normalfall. Fast nur in der Mathematik haben wir die Situation, dass Fragen nur eine Lösung zulassen.
Lesen Sie nun den Satz:
“Freude schweift in die Welt hinaus, bricht jede Frucht und kostet jeden Wein.” (Emanuel Geibel)
Ergänzen Sie nun die folgenden Buchstaben zu einem Wort:
Tr___e
Die meisten Menschen ergänzen die Buchstaben im ersten Beispiel zu ‘Träne’, während sie im zweiten ‘Traube’ lesen. Durch das vorangehende Zitat sind wir geeicht. Wir assoziieren Wein und Frucht mit Trauben, Weinen und Schreien dagegen mit Tränen. Die Voreinstellung macht den Gedanken. Dies ist das Grundprinzip unseres Denkens. Unser Denken basiert nicht auf Boolescher (Aristetolischer) Logik, wie Erkenntnistheoretiker immer noch zu denken scheinen. Ich halte es für einen unerträglichen Mangel der Erkenntnistheorie, dass sie Bayes Erkenntnisformel noch nicht zu ihrer Grundlage gemacht hat und statt dessen auf das unhaltbare Konzept des Kantschen Apriori setzt.
8. Weiterführende Literatur
Anwendungen von Bayes Formel auf dieser Homepage:
Das Doomsday-Argument
Induktionsprinzip
Solipsismus
9. Weiterführende Bücher
von Randow, Gero, ‘Das Ziegenproblem – Denken in Wahrscheinlichkeiten’, (1992), Rowohlt Taschenbuch Verlag GmbH, Reinbek bei Hamburg
Sehr unterhaltsames allgemeinverständliches Buch über alltägliche Fehlüberlegungen aus der Wahrscheinlichkeitsrechnung. Nebenbei werden die Grundbegriffe der Wahrscheinlichkeitsrechnung und Bayes Erkenntnisformel sehr anschaulich erklärt.
Wickmann, Dieter, ‘Bayes-Statistik – Einsicht gewinnen und Entscheiden bei Unsicherheit’, (1990), Bibliographisches Institut & F.A. Brockhaus AG, Mannheim
Ein Mathematiklehrbuch zur Bayes Statistik für Profis.