Sind Teilchen, die niemand sieht, real?

Visits: 1367

Philipp Wehrli, 2. Januar 2002

Viele Physiker behaupten, Teilchen besitzen nur die Eigenschaften, die wir beobachtet haben. Unbeobachtete Teilchen sind eigenschaftslos. Weshalb viele Physiker so denken, zeigt das hier beschriebene Experiment.

Die folgenden Experimente gehören wohl zu den verblüffendsten der Quantentheorie. Hauptakteure sind Teilchen mit Spin ½, z. B. Protonen, Elektronen oder Neutronen. Beobachtet wird das Verhalten der Teilchen in einem Magnetfeld. Wenn man die Teilchen in ein inhomogenes Magnetfeld stellt, wird die Hälfte der Teilchen nach oben, die andere nach unten gezogen. Die Teilchen verhalten sich also wie kleine Stabmagnete, allerdings mit der Einschränkung, dass die Richtung ihres Magnetfeldes ‘gequantelt’ ist. Sie kann nur parallel oder antiparallel zu einem äusseren Magnetfeld liegen. Schiefe Teilchen gibt es keine.

Die Ladungen und der quantenmechanische Drehimpuls (der sogenannte Spin) spielen in den folgenden Experimenten nur indirekt eine Rolle, obwohl ich vom Spin sprechen werde. Physiker nennen es Spin, wenn sie die Richtung des Magnetfelds eines Protons meinen. Der Grund ist, dass der Spin beim Proton immer in die gleiche Richtung zeigt, wie das Magnetfeld des Teilchens. (Beim Neutron und beim Elektron sind Spin und Magnetfeld antiparallel). Wenn ich im folgenden vom Spin schreibe, meine ich nichts anderes als die Richtung des Magnetfeldes des Teilchens. Wie die Richtung des Magnetfeldes ist auch die Richtung des Spins gequantelt.

Beispiel für ein inhomogenes Magnetfeld ist das Feld eines gewöhnlichen Stabmagneten. In der Praxis werden zwar Elektromagnete verwendet, aber weil die meisten Leute wissen, was ein Stabmagnet ist, ergänze ich Abbildung 1 durch einen (grauen) Stabmagneten, der deutlicher zeigt, in welche Richtung die Kraft wirkt. Im folgenden betrachte ich Protonen. Das Experiment sieht aber mit Neutronen oder Elektronen genau gleich aus.

Für das Verhalten eines Protons bei einem Stabmagneten gelten die Regeln:

1.) Gleichnamige Pole stossen sich ab.

2.) Ungleichnamige Pole ziehen sich an.

3.) Jedes Proton ist entweder parallel oder antiparallel zum äusseren Magnetfeld ausgerichtet. Andere Richtungen wurden noch nie beobachtet.

Abbildung 1 Ein Proton (symbolisch als kleiner Stabmagnet mit N und S angeschrieben) im inhomogenen Magnetfeld. Die gestrichelten Pfeile zeigen die Feldlinien des inhomogenen Magnetfeldes. Man könnte sich vorstellen, das Magnetfeld stamme von einem riesigen Stabmagneten (grau). Wird das Proton zu diesem Stabmagneten hingezogen, sagen wir, es habe in diesem Apparat Spin ‘plus’ oder positiven Spin. Wird es abgestossen, sagen wir, es habe Spin ‘minus’ oder negativen Spin.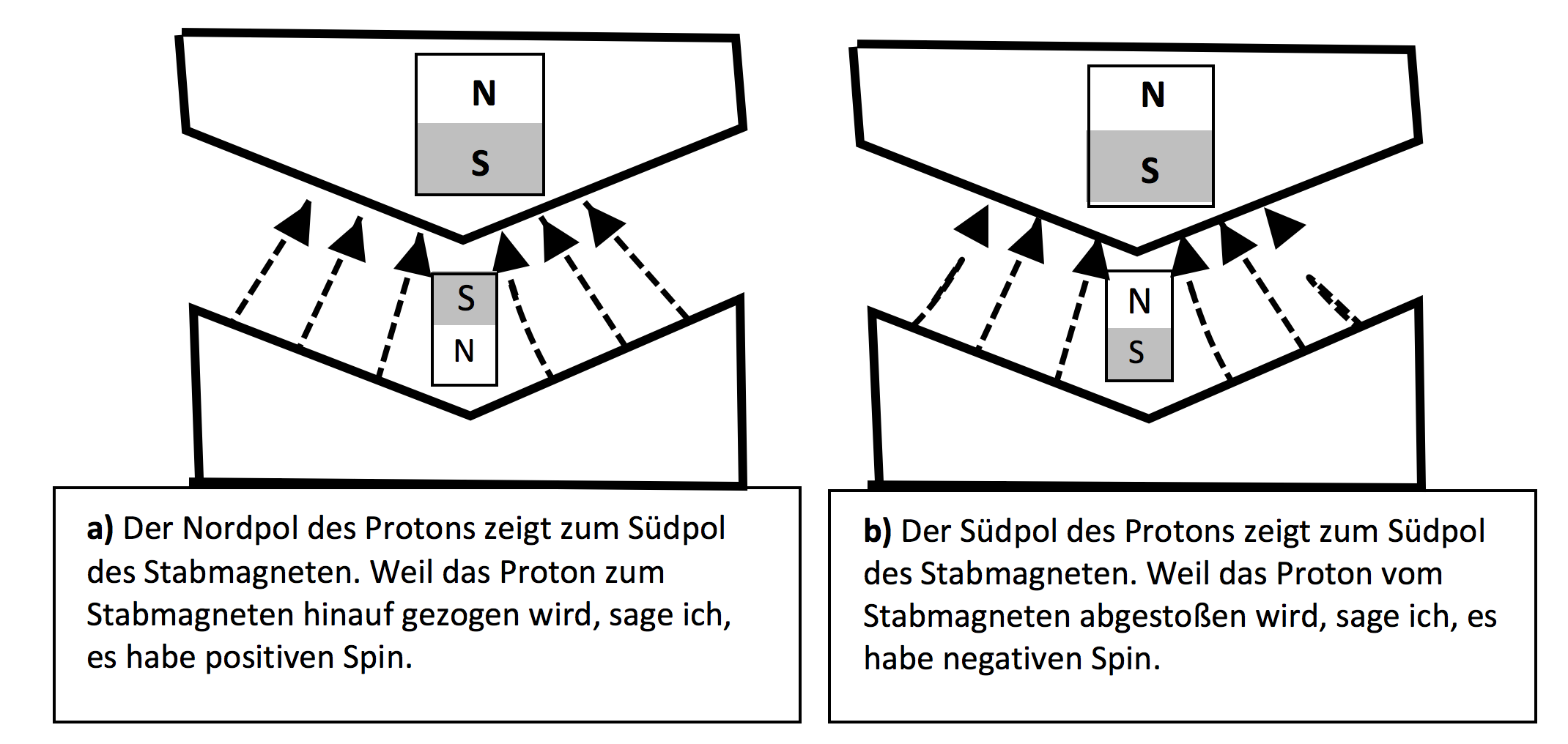

Wenn das Magnetfeld des Protons in die gleiche Richtung zeigt, wie das äussere Magnetfeld, sagen wir, das Proton habe in diesem Magnetfeld ‘positiven Spin’. Im anderen Fall sagen wir, es habe ‘negativen Spin’. Ob das Proton positiven oder negativen Spin hat, hängt also vom Apparat ab, in dem ich den Spin messe. Wenn ich den Apparat auf den Kopf stelle, ohne am Teilchen etwas zu ändern, dann hat dasselbe Teilchen im gedrehten Apparat den entgegengesetzten Spin.

Im sogenannten Stern-Gerlach Versuch kann man zeigen, dass es in jedem Magnetfeld nur diese zwei Sorten von Protonen gibt, und man kann die Protonen nach dem Spin sortieren. Dabei wird ein Protonenstrahl wie oben durch ein stark inhomogenes Magnetfeld geschickt, wobei man sieht, dass der Strahl in genau zwei Teilstrahlen aufgespalten wird.

Abbildung 2 Stern-Gerlach Versuch: Ein Protonenstrahl wird in einem inhomogenen Magnetfeld in zwei Teilstrahlen aufgeteilt. Die Protonen des einen Strahls haben ‘positiven Spin’, die des anderen ‘negativen Spin’.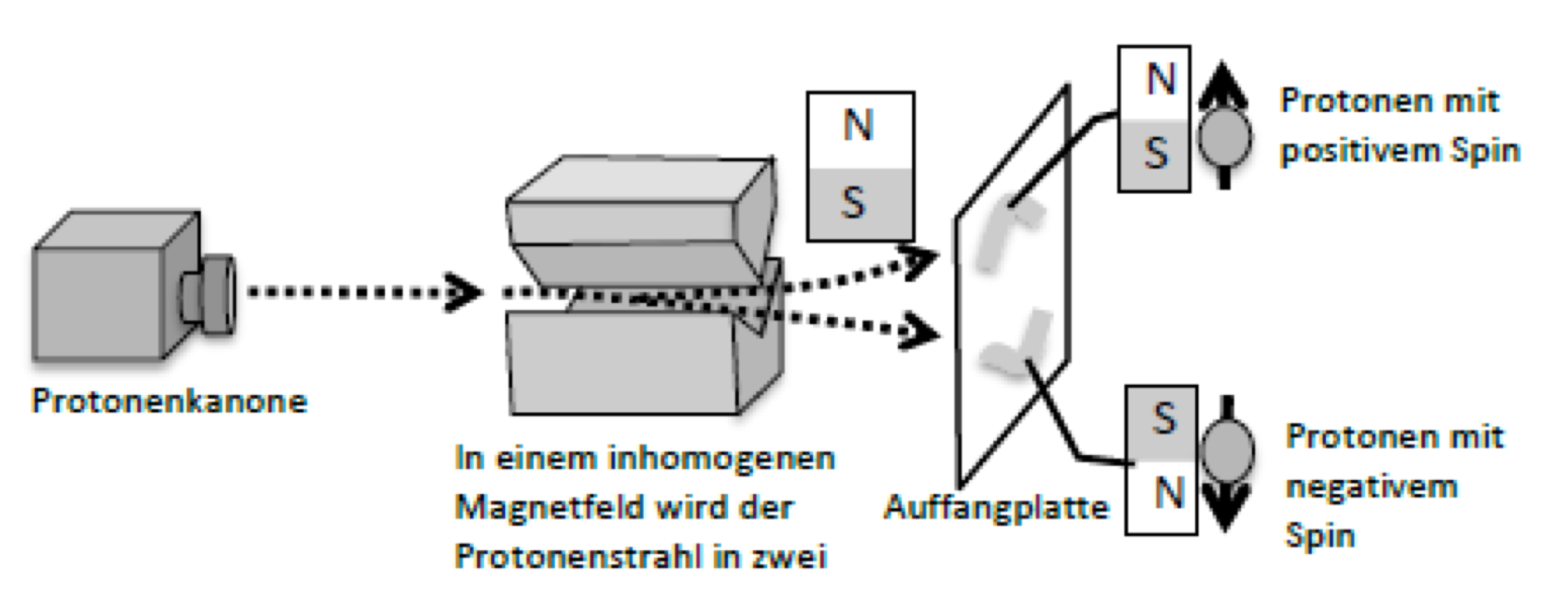

Für die weitere Verwendung zeichne ich den gleichen Versuch schematisch. Wenn das Magnetfeld in Richtung z grösser wird, nenne ich die Apparatur ‘z Polarisator’. Statt ‘positiver Spin’ schreibe ich dann ‘Spin +z’ und statt ‘negativer Spin’ schreibe ich ‘Spin -z’. Die Apparatur zeichne ich so:

Abbildung 3 Gleich wie Abbildung 2, aber schematisch. Wieder zeigt der graue Stabmagnet neben dem Apparat, wie das äussere Magnetfeld liegt. Die kleinen Stabmagnete der austretenden Strahlen zeigen, die Magnetfelder der Protonen nach dem Apparat.

Offensichtlich kann ich Polarisatoren in verschiedenen Richtungen einrichten. Einen analogen Apparat, welcher die Spinkomponente in y Richtung (y Spin) misst, nennen wir y Polarisator, und die entsprechenden Spinkomponenten +y und -y.

Nun stellen wir drei Polarisatoren hintereinander, zuerst einen z, dann einen y und am Ende wieder einen z Polarisator. Wir teilen also zuerst einen Protonenstrahl in zwei Teilstrahlen +z und -z. Dann teilen wir die -z Protonen in zwei Teilstrahlen +y und -y. Aber bei dieser zweiten Teilung verwandeln sich einige Spins von -z in +z.

Abbildung 4 Werden Protonen zuerst in einem z Polarisator sortiert und danach die Protonen mit Spin -z in einem y Polarisator sortiert, so finden sich in einem weiteren z Polarisator plötzlich wieder Protonen mit Spin -z.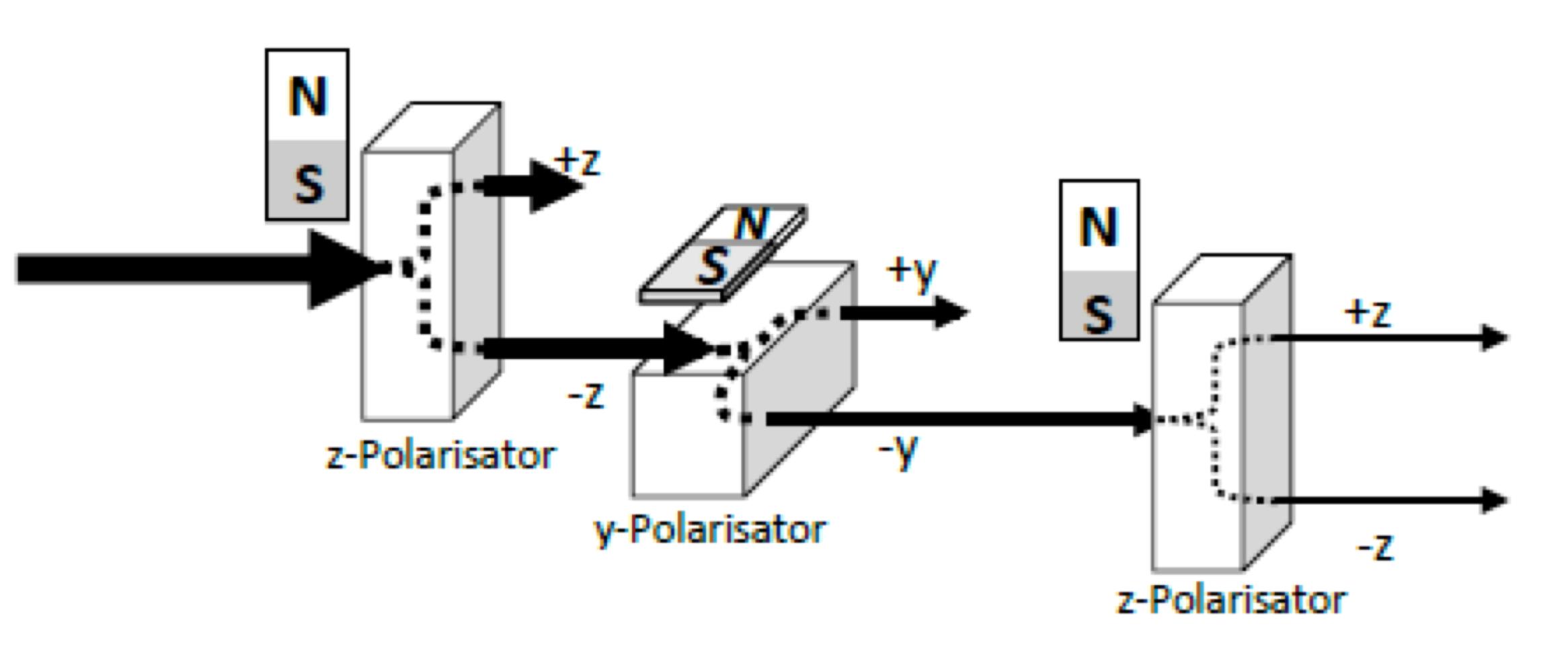

Nun, vielleicht denken Sie jetzt: Die Protonen werden eben im y Polarisator derart durchgeschüttelt, dass sie alles vergessen, was vorher war. Die Protonen haben aber überhaupt nichts vergessen, wie das folgende Experiment zeigt. Wir können nämlich den +y und den -y Strahl wieder zusammenleiten und gemeinsam in einen z Polarisator lenken. Wenn wir das tun, ‘erinnern’ sich die Protonen plötzlich wieder daran, dass sie eigentlich -z Spin haben. Es gibt keinen +z Strahl mehr.

Mit anderen Worten: Im -y Strahl hat es +z Protonen und im +y Strahl hat es +z Protonen, aber in beiden Strahlen zusammen hat es keine +z Protonen.

Abbildung 5 Wenn nach dem y-Polarisator die Teilstrahlen +y und -y wieder zusammengeführt werden, findet man in diesen beiden Strahlen zusammen nur Protonen mit Spin -z. Dies, obwohl im Teilstrahl -y alleine einige Protonen Spin +z haben (wie in Abbildung 4 gezeigt).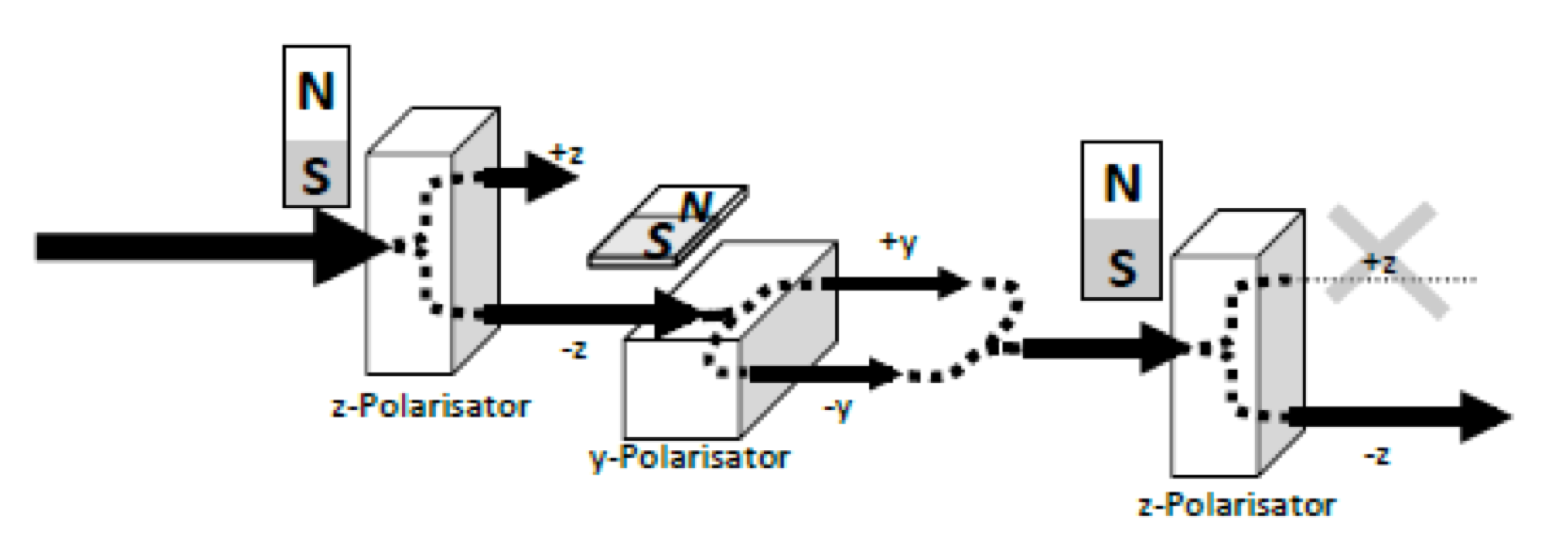

In der Quantenphysik gibt es viele Paare von Messgrössen, die ein ähnliches Verhalten zeigen, wie ich es eben am Beispiel des y und des z Spins des Protons gezeigt habe. Die beiden Messgrössen eines solchen Paares nennt man komplementär. Sie können nicht gleichzeitig exakt gemessen werden. Andere Beispiele von komplementären Grössen sind die Paare von Grössen, die über die Heisenbergsche Unbestimmtheitsrelation zusammenhängen, also Ort und Impuls eines Teilchens, Zeit und Energie etc..

Wie auch im Doppelspaltversuch dürfen wir auch in den obigen Experimenten den Teilchen nicht eine Eigenschaft zuschreiben, die wir nicht gemessen haben. Im Doppelspaltversuch dürfen wir nicht sagen, das Elektron sei durch den einen oder den anderen Spalt gegangen, wenn wir es nicht bei einem Spalt (z. B. mit einer Lampe) beobachtet haben. Ein unbeobachtetes Elektron geht immer durch beide Spalte, was zu einem Interferenzmuster führt. Ebenso können wir in Abbildung 5 nicht sagen, das Proton habe im y Polarisator entweder einen Spin +y oder -y. Denn wir führen ja die Teilstrahlen wieder zusammen, ohne zu schauen, wo das Proton ist. Jedes Proton geht im y Polarisator beide Wege gleichzeitig. Deshalb kommt es im z Polarisator zur Interferenz, wobei der +z Strahl ausgelöscht wird. Wenn wir keine Messung in y-Richtung durchführen, ist der Spin in y-Richtung auch nicht festgelegt.

Es ist nicht nur so, dass ein Teilchen an zwei Orten gleichzeitig sein kann. Die Experimentatoren können sogar erst im Nachhinein entscheiden, ob das Teilchen an beiden Orten war oder nur an einem. Denn wenn Sie die Strahlen +y und -y zusammenführen, hat das Teilchen die Information von beiden Wegen. Wenn sie dagegen beide Teilstrahlen einzeln anschauen, dann erscheint das Teilchen immer nur in einem von ihnen.

Niels Bohr, Werner Heisenberg und einige andere bestanden energisch darauf, dass ein Teilchen nur dann an einem bestimmten Ort ist, wenn wir es an diesem Ort messen. Diese Vorstellung nennt man die ‘Kopenhagener Deutung’ (Sel 1). Einstein, Bohm, deBroglie und Schrödinger wehrten sich ebenso energisch gegen diese Vorstellung. Sie sagten, ein Teilchen ist immer nur an einem Ort. Wir wissen nur nicht, nach welchen Gesetzen es sich im Kleinen bewegt. Was denken Sie dazu, wenn Sie das obige Experiment betrachten?

Weiterführende Artikel auf dieser Homepage:

Der Beobachter in der Quantentheorie
Einstein-Podolsky-Rosen Experiment

 Was hat Quantenphysik mit Telepathie zu tun? Wehrli (Vorstandsmitglied) geht in seinem Vortrag an der Generalversammlung der Skeptiker Schweiz auf pseudowissenschaftliche Behauptungen von sogenannten “Telepathen” und ähnlichen Menschen ein.

Weiterführende Bücher:

Philip Wehrli, ‘Das Universum, das Ich und der liebe Gott’, (2017), Nibe Verlag,

In diesem Buch präsentiere ich einen Gesamtüberblick über mein Weltbild: Wie ist das Universum entstanden? Wie ist das Leben auf der Erde entstanden? Was ist Bewusstsein und woher kommt es? Braucht es dazu einen Gott?
Viele Artikel dieses Blogs werden in diesem Buch in einen einheitlichen Rahmen gebracht, so dass sich ein (ziemlich) vollständiges Weltbild ergibt.

Leserunde bei Lovelybooks zum Buch ‘Das Universum, das Ich und der liebe Gott’, von Philipp Wehrli (abgeschlossen)

Rezensionen bei Lovelybooks
Rezensionen bei Amazon
Film-Präsentation zum Buch
Nibe Verlag

 

 

Audretsch Jürgen (Hrsg.), ‘Verschränkte Welt – Faszination der Quanten’, (2002), WILEY-VCH, Weinheim
Eine Sammlung anregender Artikel zum aktuellen Stand der Quantenforschung und ihren neuesten Anwendungen, die Quantenkryptographie und den Quantencomputer. Auch die Probleme bei der Interpretation werden geschildert und mit der Dekohärenztheorie wird eine mögliche Lösung angedeutet. Den vollen Genuss hat aber nur, wer die Quantentheorie schon kennt.

Rae Alastair, ‘Quantenphysik: Illusion oder Realität?’, (1996), Reclam
Vielleicht die einfachste Erklärung zum Einstein-Podolsky-Rosen Experiment, die ich kenne.

Selleri Franco, (1990) ‘Die Debatte um die Quantentheorie’, Vieweg, Braunschweig
Sellerie zeigt die Interpretationsprobleme, die durch die Quantentheorie aufgeworfen wurden und erklärt, wie sie von den Begründern der Theorie gelöst wurden und wie die Interpretationen heute z. T. mit Experimenten überprüft werden können. Dabei verwendet er ziemlich abstrakte Mathematik. Man kann zwar über die meisten Formeln hinweglesen, aber das Buch verliert dabei natürlich etwas.

Spektrum Akademischer Verlag, Heidelberg, ‘Quantenphilosophie – Reihe Verständliche Forschung’, Neuser / Neuser-von Oettingen (Herausgegeber)
Wer sich für die Philosophie hinter der Quantentheorie interessiert, findet hier ein breites Spektrum anregender Artikel, unter anderem von Schrödinger, Gamov, d´Espagnat, Cassidy und de Witt. Die Artikel sind kurz, prägnant und allgemeinverständlich und werden mit vielen schönen Grafiken illustriert.