Visits: 1883
Philipp Wehrli, 2. Januar 2002
Einsteins berühmte Relativitätstheorie revolutionierte unsere Vorstellung von Raum und Zeit. Die spezielle Relativitätstheorie beschreibt die Bewegungen im gravitationsfreien Raum, während die allgemeine Relativitätstheorie die Gravitation als ein Phänomen erklärt, das durch die Krümmung der Raumzeit entsteht. Hier stelle ich einige erstaunliche Effekte der allgemeinen Relativitätstheorie vor. Was Krümmung der Raumzeit bedeutet und wie sie die Gravitation verursacht, wird in der Seite Gravitation angedeutet.
1. Uhren im Gravitationsfeld
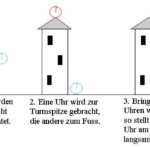
Wie bereits im Artikel zur speziellen Relativitätstheorie erwähnt, müssen wir zwei Fälle unterscheiden, in denen Uhren langsamer gehen. Beim ersten Fall handelt es sich um schnell bewegte Uhren, die in der speziellen Relativitätstheorie beschrieben werden. Der zweite Fall, der in der allgemeinen Relativitätstheorie beschrieben wird, soll hier diskutiert werden. Wieder werden zwei genau gleiche Uhren exakt gleich gerichtet. Diesmal bringt Andi die eine Uhr auf einen hohen Turm, während Betti die andere zum Fuss des Turmes schafft. Dort angekommen warten beide einige Zeit, um schliesslich mitsamt den Uhren wieder zur Mitte des Turmes zusammenzukommen, wo sie die Uhren vergleichen. Dort stellen die zwei erstaunt fest, dass die Uhr, die auf der Turmspitze lag, schneller gelaufen ist als die Uhr am Fuss des Turmes.
Abbildung 1 Uhren im Gravitationsfeld gehen langsamer. Je weiter unten die Uhr ist, desto langsamer geht sie.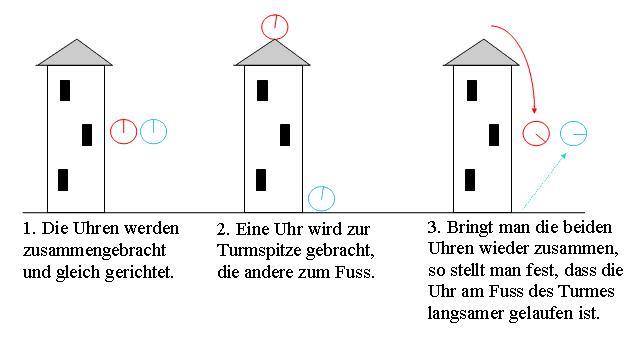
Der Effekt ist umso grösser, je stärker das Gravitationsfeld ist. Mit sehr genauen Uhren ist der Effekt auch auf der Erde auf Bergen messbar. Bei schnell fliegenden Satelliten wirken beide besprochenen Effekte der Zeitverlangsamung. Weil der Satellit schnell fliegt, läuft die Uhr langsamer. Weil er hoch oben ist, läuft sie schneller. Die beiden Effekte überlagern sich und je nach Flugbahn überwiegt der eine oder der andere. Die Messungen stimmen exakt mit der Theorie überein.
2. Rotverschiebung im Gravitationsfeld
Die Verlangsamung der Zeit im Gravitationsfeld kann auch unter einem anderen Gesichtspunkt gesehen werden. Das Licht ist eine elektromagnetische Welle, es hat also eine Frequenz. Licht von niedriger Frequenz hat wenig Energie und ist rot. Licht von hoher Frequenz ist blau und hat eine hohe Energie.
Nun könnten wir aber von einem Turm eine Lichtwelle ‘fallenlassen’. Beim ‘Fallenlassen’ wird das Licht zwar nicht schneller, denn die Lichtgeschwindigkeit ist überall und immer c = 299’792 km/s. Das Licht erhält aber doch mehr Energie, es wird also bläulicher und hat unten eine höhere Frequenz als oben.
Dieses Licht kann nun zum direkten Uhrenvergleich verwendet werden. Nehmen wir an, beim obigen Experiment mit den Uhren auf und unter dem Turm werde zusätzlich folgendes gemacht. Gerade wenn sich Andi und Betti verabschieden, beginnt Andi eine Lichtwelle auszusenden, die Betti mit einem Spiegel wieder zurückwirft. Betti zählt die Wellenbuckel, die auf den Spiegel treffen. Andi zählt die Wellenbuckel, die er aussendet und die, die er vom Spiegel her wieder empfängt. Sie stellen fest, dass keine Wellenbuckel verlorengehen. Andi sendet also gleich viele Buckel aus, wie Betti reflektiert und wie er auch wieder empfängt.
Allerdings sagt Betti mit Blick auf ihre kaum fortgeschrittene Uhr: „Die Wellenbuckel sind wahnsinnig rasch hintereinander gekommen. Das Licht hatte eine sehr hohe Frequenz und war ganz blau.“
Andi meint dagegen: „Nein, ich habe Licht mit einer niedrigen Frequenz losgeschickt und auch wieder solches empfangen. Das Licht war ganz rot.“
Die drei scheinbar verschiedenen Effekte sind also nur verschiedene Aspekte eines einzigen Effektes:
1.) Aufsteigendes Licht wird rot, herunterfallendes wird blau.
2.) Herunterfallendes Licht und herunterfallende Teilchen werden energiereicher.
3.) Die Zeit läuft unten langsamer als oben.
Die Verlangsamung der Zeit in der Nähe von Massen und das Herunterfallen von Gegenständen hängt sogar untrennbar zusammen, wie Einstein zeigte (Eps 1). Immer wenn in einem Gebiet des Raumes die Zeit langsamer läuft, fallen alle Gegenstände in dieses Gebiet hinein. Es braucht dazu gar keine Kraft mehr. In einem Spezialfall ist dies sogar sehr einfach zu verstehen, nämlich wenn Licht im Gravitationsfeld abgelenkt wird.
3. Die Formeln für Rotverschiebung und Zeitdilatation im Gravitationsfeld
Angenommen, wir lassen ein Lichtteilchen von einem Turm fallen, das heisst, wir leuchten mit einer Lampe von einer Turmspitze zum Erdboden hinunter. Wie ändert sich dabei die Frequenz des Lichtes? (Eine ausführliche Rechnung findet man in (Sex 3).
Die Energie des Photons ist E=hn (h ist die Plancksche Konstante). Dieser Energie entspricht die Masse
m = E / c2 = hν /c2 (1)
Wenn diese Masse von einem Turm der Höhe Δx hinunterfällt, gewinnt sie die Energie ΔE, so dass sich die Frequenz des Lichtes um Δν ändert (g ist die Gravitationsbeschleunigung):
ΔE = mgΔx = hΔν (2)
Die obige Herleitung gilt für kleine Δx und kleine Gravitationskraft. Fällt das Photon sehr weit hinunter, so verändert sich dabei seine Frequenz und die dazugehörige Masse zu stark, so dass ich m nicht mehr als konstant annehmen darf. Ich kann also auf diese Weise z. B. nicht den Radius eines schwarzen Lochs herleiten, aber auf der Erde ist die Frequenzänderung so klein, dass die Herleitung sehr exakt ist.
Aus (1) und (2) erhalte ich die relative Frequenzänderung:
Δν / ν = gΔx / c2 (3)
Diese Frequenz kann ich nun dazu benützen, zwei Uhren zu vergleichen. Angenommen, eine Atomuhr A liege oben auf dem Turm und messe die Zeit to. Unten auf der Erde steht ein Physiker mit zwei weiteren Uhren B1 und B2, welche die Zeiten t1 und t2 anzeigen. B1 ist genau gleich gebaut wie die Uhr A auf dem Turm. Beide haben je ein eigenes Atom eingebaut und sie messen die Zeit, indem sie zählen, wie oft dieses Atom schwingt. Die Uhr auf dem Turm sendet ausserdem im Rhythmus der Atomschwingungen ein Signal der Frequenz n zu B2. Die Uhr B2 wird durch das Signal von A gerichtet, sie zählt also nicht die Schwingungen eines eingebauten Atoms, sondern die Schwingungen des Signals von A. Da kein Wellenberg verloren geht und da wir die Messung über eine beliebig lange Zeit weiter führen können ohne dass sich der Abstand zwischen den Uhren verändert, können wir sagen, B2 zeigt ebenfalls die Zeit an, die auf dem Turm vergeht. Wir können also die “Geschwindigkeit” der Zeit oben und unten auf dem Turm vergleichen, indem wir die Uhren B1 und B2 vergleichen.
Da die Frequenz des Signals beim Herunterfallen grösser wird, läuft B2 schneller als B1 und zwar gilt:
(ν + Δν) / t2= ν / to = ν / t1 (4)
Die Begründung für diese Gleichung ist klar: Die Zeiten to, t1 und t2 sind umso grösser, je grösser die Frequenz ist, mit der sie weiter zählen. Die Gleichung
ν / to = ν / t1 zeigt, dass der Beobachter unten am Turm nicht das Gefühl hat, seine Zeit laufe langsamer. Seine Zeiteinheit ist definiert durch die Schwingung des Atoms in der Atomuhr B1 und die Frequenz dieser Schwingung nennt er ν. Genau gleich kommt der Beobachter bei A zum Schluss, das Atom seiner Uhr schwinge mit der Frequenz n. Mit der so definierten Zeiteinheit erscheint der Zeitablauf beiden Beobachtern gleich: Beide können in einer Stunde gleich viel Arbeiten erledigen oder gleich viele Sachertorten essen. Dass ein Unterschied besteht, merken sie erst, wenn A ein Signal hinunter schickt und offensichtlich wird, dass das n von A nicht das gleiche ist wie das ν von B. Das ν von A kommt in der Uhr B2 als (ν + Δν) an. Dies ist gemeint, wenn jemand sagt: “Die Zeit läuft unten im Gravitationsfeld langsamer”.
Die Uhr B2 misst sozusagen die Zeit oben auf dem Turm in Einheiten unten auf der Erde. Die Anzeige der Uhr B2 wird dann als die Zeit angesehen, die bei A vergangen ist, während die Anzeige der Uhr B1 mit der Zeit unten identifiziert wird. (4) wird deshalb oft so geschrieben:
Toben = (ν + Δn) / ν Tunten (5)
Oder mit (3):
Toben = (1+gΔx/c2)Tunten (6)
Wie bereits erwähnt gelten alle diese Formeln nur für kleine Höhenunterschiede r und kleine Gravitationsbeschleunigungen g. Aus der Beschleunigung im Gravitationsfeld können wir also die Formel für die Zeitdilatation herleiten. Im Artikel Gravitation zeige ich, wie wir auch hätten umgekehrt argumentieren können. Wir hätten die Zeitdilatation als gegeben annehmen können und daraus die Gravitationsbeschleunigung herleiten können. Dies ist eigentlich die viel überraschendere Schlussfolgerung: Weil die Zeit unten langsamer läuft, fallen die Gegenstände hinunter. Ein Vorgeschmack, wie dies gehen könnte, im folgenden Abschnitt.
4. Lichtablenkung im Gravitationsfeld
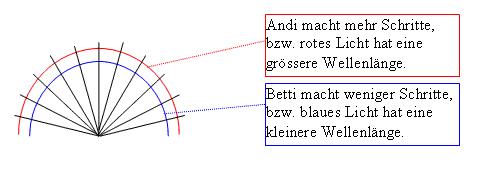
Nehmen wir an, Andi und Betti spazieren zusammen. Sie gehen immer beide gleich schnell, sagen wir, sie machen beide zwei Schritte zu 50 Zentimeter pro Sekunde. Sie machen eine Bergwanderung. Dabei gehen sie anfangs den Höhenlinien nach, und Betti geht immer etwas weiter unten als Andi. Nun geschieht folgendes. Weil Betti weiter unten geht, läuft ihre Uhr etwas langsamer als die von Andi. Deshalb schreitet Betti auch etwas langsamer. Wenn die beiden dennoch immer schön nebeneinander bleiben wollen, werden sie also einen Bogen zu Betti hin machen, also nach unten.
Dasselbe geschieht, wenn Licht horizontal über eine grosse Masse fliegt. Die Wellenlänge unten ist blauverschoben, also kürzer. Die Wellenlänge oben ist rotverschoben, also länger. Dies führt dazu, dass das Licht abgelenkt wird.
Wenn ein Stern sehr dicht und schwer ist, wird in einem ganz bestimmten Abstand von diesem Stern das Licht so stark abgelenkt, dass es einen vollständigen Kreis beschreibt. Der Radius dieses Kreises ist das 1½-fache des Schwarzschildradius’. Dieser Spezialfall ist in Abbildung 10 gezeichnet. Wer auf diesem Kreis steht, kann sich auf den eigenen Hinterkopf schauen. Weil dies in allen Richtungen gleichermassen gilt, ist das Bild des Kopfes dann eigentlich über den ganzen Horizont verschmiert.
Die Ablenkung des Lichtes im Gravitationsfeld wurde zum ersten mal während einer Sonnenfinsternis von Sir Arthur Eddington und in einer zweiten Messung von Arthur Dyson beobachtet. Als im Jahre 1916 die Sonne vollständig vom Mond verdeckt war, zeigten die beiden, dass das Licht von Sternen, die eigentlich hinter der Sonne lagen, so um die Sonne herumgebogen wurde, dass die Sterne dennoch sichtbar waren. Dieser Effekt war grösser als Newtons Gravitationstheorie ihn voraussagte und stimmte gut mit Einsteins Theorie überein. Seither gibt es wesentlich genauere Messungen, die ebenfalls die allgemeine Relativitätstheorie bestätigen.
Weil grosse Massen Licht ablenken, können wir manchmal Lichtquellen (z. B. Quasare) sehen, die eigentlich hinter einer Galaxie versteckt sein müssten. Durch die Lichtablenkung sehen wir die Lichtquellen dann ringförmig um die dazwischenliegende Galaxie verschmiert. Die Galaxie nennt man dann eine ‘Gravitationslinse’.
Abbildung 3 Typische Konstellation einer Gravitationslinse. Eine helle Lichtquelle liegt hinter einer Galaxie. Ihre Lichtstrahlen (durchgezogene gebogene Linien) werden von der Galaxie abgelenkt. Der Beobachter sieht das Licht aus zwei oder noch mehr verschiedenen Richtungen ankommen und vermutet daher mehrere Quellen (gestrichelte Linien).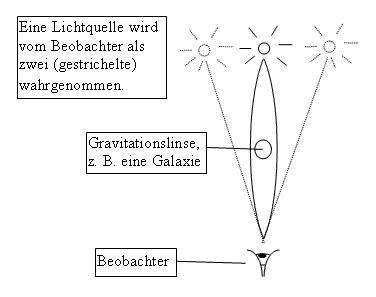
Dieser Effekt der Lichtablenkung ist noch bedeutsamer als es auf den ersten Blick den Anschein macht. Für alle unsere Sinne und für all unsere Messgeräte zeigen die Lichtstrahlen immer den kürzesten und schnellsten Weg an. Wenn in Abbildung 3 das Licht nicht geradeaus fliegt, dann deshalb, weil der kürzeste und schnellste Weg nicht geradeaus führt.
Dies führt zu ganz verblüffenden Effekten. Wenn wir mit dem Auto eine Kurve fahren, dann spüren wir, wie wir nach aussen gezogen werden. Je schneller wir fahren, desto mehr zieht es uns nach aussen. In der Nähe eines schwarzen Loches (näher als 1½ des Schwarzschildradius) ist es genau umgekehrt: Wenn wir schneller fahren, werden wir zusätzlich nach innen gezogen. Die ‘Zentrifugalkraft’ zieht hier nicht nach aussen, sondern nach innen.
Ein anderer Effekt kann mit einem Kreiselkompass (Gyroskop) beobachtet werden. In der Newtonschen Physik zeigt ein Kreiselkompass in einem Satelliten oder einer Rakete immer in die gleiche Richtung im Raum, egal, wie das Raumschiff bewegt oder beschleunigt wird. In der allgemeinen Relativitätstheorie ist dies völlig anders. Richten wir z. B. die Achse eines Kreiselkompasses in die Richtung, in die das Licht fliegt, und folgen wir den Lichtstrahlen, dann zeigt der Kreisel immer genau in die Richtung des Lichtes, auch wenn die Lichtstrahlen in einem Gravitationsfeld abgelenkt werden.
Abbildung 4 a) Wenn ich mit dem Auto eine Kurve fahre, spüre ich eine Kraft, die mich nach aussen zieht. Ein Kreiselkompass, den ich im Auto aufhänge, zeigt nach der Kurve noch immer auf denselben Stern am Fixsternhimmel wie vor der Kurve. Relativ zum Auto hat sich der Kreisel aber gedreht.
b.) Folge ich dagegen mit einer Rakete dem Weg eines Lichtstrahls, so spüre ich keine Kraft, die mich nach aussen zieht, egal wie schnell ich fahre. Dies gilt auch, wenn der Lichtstrahl von einer Masse abgelenkt wird und deswegen eine Kurve oder sogar einen Kreis durchläuft. Mein Kreiselkompass zeigt während des ganzen Weges in die Richtung des Lichtstrahls, wenn ich ihn einmal so ausgerichtet habe. Wenn ich einem gekrümmten Lichtstrahl folge, dreht sich der Kreisel relativ zum Fixsternhimmel, aber nicht relativ zur Rakete.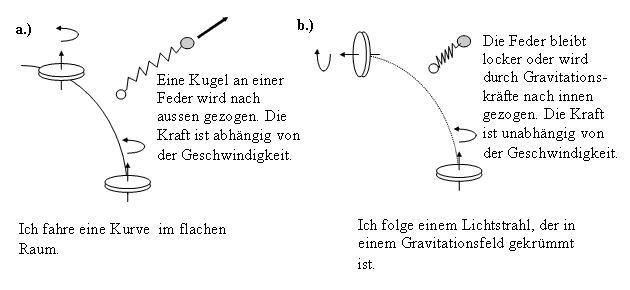
Dass Lichtstrahlen von einer Masse abgelenkt werden, könnte man sich auch in Newtons Physik vorstellen. In der allgemeinen Relativitätstheorie ist dieser Effekt viel umfassender. Es werden nicht nur die Lichtstrahlen abgelenkt, sondern sämtliche Naturgesetze folgen einer völlig neuen Geometrie. Man könnte sagen: Die Lichtstrahlen verfolgen immer noch die geradest möglichen Linien. Aber der Raum oder besser gesagt, die Raum-Zeit, ist gekrümmt. Siehe dazu auch Gravitation und Kosmologie.
5. Schwarze Löcher
In der Nähe von grossen Massen ist die Verlangsamung der Zeit grösser. Wenn ein Stern sehr dicht zusammengepackt ist, gibt es sogar einen bestimmten Abstand, bei dem die Zeit völlig stillsteht. Diesen Abstand nennt man nach dem deutschen Astronomen Karl Schwarzschild den Schwarzschildradius. Weil die Zeit völlig stillsteht, kann kein Licht von dort entweichen. Wenn wir von aussen zuschauen würden, wie ein Astronaut auf den Stern hinabfällt, würden wir sehen, wie er immer rötlicher wird und sich immer langsamer bewegt, je näher er dem Schwarzschildradius kommt. Beim Schwarzschildradius scheint der Astronaut sozusagen ‘anzufrieren’, obwohl er noch immer im freien Fall ist. So lange wir ihm auch zuschauen, wir werden nie sehen können, wie er den Schwarzschildradius überschreitet. Wir sehen das Licht, das von ihm ausgeht, zunehmend rotverschoben, bis es schliesslich so rotverschoben ist, dass wir gar kein Licht mehr sehen.
Aus dem Gebiet innerhalb des Schwarzschildradius, kann überhaupt nichts mehr entweichen, nicht einmal mehr Licht (von aussen gesehen fällt ja auch nichts hinein). Weil solche Sterne kein Licht mehr aussenden, nennt man sie ‘schwarze Löcher’. In Russland werden sie ‘gefrorene Sterne’ genannt.
Für den hineinfallenden Astronauten sieht die Sache ganz anders aus. Er bemerkt nämlich gar nicht, dass seine Zeit stillsteht und dass für uns draussen unendlich viel Zeit vergeht. Er hat im Gegenteil das Gefühl, er falle mit zunehmender Geschwindigkeit ins schwarze Loch hinein (Sex 3).
Im Zusammenhang mit schwarzen Löchern können verschiedene physikalische Grössen unendlich gross oder unendlich klein werden. Diese Unendlichkeiten nennen die Physiker Singularitäten. Roger Penrose postulierte, dass es eine kosmische Zensur gebe, die verhindere, dass wir solche Singularitäten sehen können. Die Unendlichkeiten können seiner Ansicht nach nur im Inneren des schwarzen Lochs auftreten, so dass wir sie nicht sehen können. In kürzerer Zeit versuchten Physiker, den Ablauf der Entstehung schwarzer Löcher genau zu beschreiben. Dabei stellte sich in fast allen Modellen heraus, dass es durchaus sichtbare Singularitäten geben kann, vor allem dann, wenn der kollabierende Stern nicht exakt kugelsymmetrisch ist. Physiker nennen solche sichtbaren Unendlichkeiten nackte Singularitäten (externer Link: Spektrum der Wissenschaft).
6. Weitere Effekte der allgemeinen Relativitätstheorie
Wie kann der Raum gekrümmt sein?
Urknall
Gravitation
7. Weiterführende Bücher:
Einstein Albert, ‘Über die spezielle und die allgemeine Relativitätstheorie, gemeinverständlich’, Springer, (1916)
Nach wie vor eine der besten Einführungen in die Relativitätstheorie, das Werk von ihrem Schöpfer selbst.
Sexl Roman u. Hannelore, ‘Weisse Zwerge – Schwarze Löcher’, (1979), Vieweg Studium, Braunschweig
Wie alle Bücher von Sexl didaktisch hervorragend und sehr sorgfältig geschrieben. Ideal als erster Kontakt mit der allgemeinen Relativitätstheorie. Verwendet einige einfache mathematische Formeln.
Epstein Lewis C., ‘Relativitätstheorie anschaulich dargestellt’, Birkhäuser, (1983), Basel
Von diesem Buch bin ich begeistert! Ohne Mathematik zeigt Epstein, wie die Krümmung der Raumzeit zur Gravitationskraft führt, wie die Lichtablenkung an grossen Massen zustande kommt und wie schwarze Löcher funktionieren.
Oloff Rainer, ‘Geometrie der Raumzeit – Eine mathematische Einführung in die Relativitätstheorie’, (1999), Vieweg, Braunschweig
Das Buch ist geschrieben für Studenten der Mathematik oder Physik, die in einem einsemestrigen Kurs von zwei Doppelstunden plus Übungen die allgemeine Relativitätstheorie wirklich verstehen wollen. Oloff erklärt bei jeder Definition und jedem Satz, wozu er sie braucht. Die Erklärungen sind anwendungsorientiert und verständlich. Ein ausgezeichnetes Buch für Physikstudenten!
Philip Wehrli, ‘Das Universum, das Ich und der liebe Gott’, (2017), Nibe Verlag,

In diesem Buch präsentiere ich einen Gesamtüberblick über mein Weltbild: Wie ist das Universum entstanden? Wie ist das Leben auf der Erde entstanden? Was ist Bewusstsein und woher kommt es? Braucht es dazu einen Gott?
Viele Artikel dieses Blogs werden in diesem Buch in einen einheitlichen Rahmen gebracht, so dass sich ein (ziemlich) vollständiges Weltbild ergibt.
Leserunde bei Lovelybooks zum Buch ‘Das Universum, das Ich und der liebe Gott’, von Philipp Wehrli (abgeschlossen)
Rezensionen bei Lovelybooks
Rezensionen bei Amazon
Film-Präsentation zum Buch
Nibe Verlag