Visits: 2389
Philipp Wehrli, 2. Janaur 2002
Das Einstein-Podolsky-Rosen Experiment stellt wohl den Höhepunkt der Quantenphilosophie dar. Es scheint, dass zwei Teilchen über weite Distanzen miteinander in Kontakt bleiben können. Die Messung am einen Teilchen scheint das Messresultat am anderen, weit entfernten Partnerteilchen zu beeinflussen. Ich stelle das Experiment vor und zeige, dass es entgegen der Lehrmeinung durchaus lokal-realistisch beschrieben werden kann, und zwar mit der Viele-Welten-Interpretation.
Für diesen Text ist ein gutes Verständnis der Polarisation von Licht Voraussetzung.
1. Die Philosophie hinter dem Experiment
Einstein, Podolsky und Rosen (EPR) wollten mit einem Gedankenexperiment zeigen, dass die Quantentheorie unvollständig sei. Sie behaupteten (in meinen Worten): Die Wahrscheinlichkeiten, die in der Quantentheorie auftreten, beruhten nur auf unserem Unwissen. Wenn wir eine vollständige Theorie hätten und alle Informationen über die Realität besitzen würden, würden die Wahrscheinlichkeiten verschwinden, denn “Gott würfelt nicht”. EPR empfanden die Annahme einer zufälligen Wirkung als unwissenschaftlich, als eine Kapitulation. Sollen wir glauben, dass jedes Mal, wenn ein Quantenereignis stattfindet, eine übernatürliche Kraft, vielleicht sogar ein Gott, eingreift? Wer oder was entscheidet, welche Möglichkeit verwirklicht wird? Woher kommt die Information darüber, wie die Welt im nächsten Augenblick aussehen wird?
EPR glaubten, dass die Welt mit einer vollständigen, lokal-realistischen Theorie beschrieben werden könne. Das heisst, sie setzten die folgenden drei Annahmen voraus:
A1. Einsteinsches Realitätskriterium
Kann man den Wert einer physikalischen Größe mit Sicherheit (das heißt mit der Wahrscheinlichkeit 1) vorhersagen, ohne ein System dabei in irgendeiner Weise zu stören, dann gibt es ein Element der physikalischen Realität, das dieser physikalischen Größe entspricht.
A2. Vollständigkeit
In einer vollständigen Theorie muss jedes Element der physikalischen Realität eine Entsprechung haben.
A3. Lokalität
Keine Information und keine Wirkung kann sich schneller ausbreiten als mit Lichtgeschwindigkeit.
Das EPR-Gedankenexperiement sollte zeigen, dass die Quantentheorie keine vollständige, lokal-realistische Theorie ist. Die Autoren erwarteten, dass die Quantentheorie ergänzt werde, damit sie vollständig sei. Es kam aber anders. Das Experiment wurde unterdessen mehrmals durchgeführt, und die meisten Physiker sind heute der Ansicht, dass es überhaupt keine lokal-realistische Theorie geben kann, welche die EPR-Experimente richtig erklärt.
2. Das Experiment
Es gibt verschiedene Varianten des EPR-Experimentes. Die folgenden Elemente sind in allen Varianten gleich:
– Zwei Teilchen werden miteinander verschränkt oder so erzeugt, dass sie miteinander verschränkt sind (was das genau bedeutet, wird unten erklärt).
– Die Teilchen werden an zwei verschiedene Orte gebracht.
– An den Teilchen werden komplementäre Grössen gemessen.
– Dieser Vorgang wird mit mehreren Teilchenpaaren wiederholt. Die statistische Auswertung aller Messresultate zeigt ein Ergebnis, das mit keiner lokal-realistischen Theorie erklärt werden kann.
2.1. Verschränkte Photonen herstellen
Im folgenden Experiment, das auch tatsächlich durchgeführt wurde, betrachten wir Paare von speziell präparierten Photonen. Die Präparation erfolgt ganz grob gesagt so: Wir nehmen ein Quecksilber- oder ein Calcium-Atom, das drei verschiedene Niveaus, also drei mögliche Elektronenbahnen hat. Dabei sind in der mittleren Elektronenbahn für das Elektron drei verschiedene Zustände 2a, 2b und 2c möglich, die alle dieselbe Energie haben, die sich aber in der sogenannten ‘magnetischen Quantenzahl’ unterscheiden. Physiker sagen, das mittlere Niveau ist ‘dreifach entartet’.
Ein Elektron, das im obersten (3.) Niveau ist, kann nicht direkt in das unterste (1.) fallen, weil dabei der Drehimpuls nicht erhalten wäre. Es kann aber auf drei verschiedenen Wegen über den mittleren Zustand zum tiefsten gelangen, nämlich über 2a, 2b oder 2c. Beim Übergang vom 3. zum 2. Niveau wird ein Photon ausgesendet und beim Übergang vom 2. zum 1. Niveau ebenso. Die beiden Photonen fliegen in entgegengesetzter Richtung auseinander. Das Spannende ist nun, dass die zwei ausgestrahlten Photonen immer in dieselbe Richtung polarisiert sein müssen. Wenn das Quecksilber-Atom geeignet ausgerichtet ist, sind die Photonen bei den Wegen über 2a oder 2c in y-Richtung polarisiert, beim Weg über 2b beide in z-Richtung. Diese Art, zwei Photonen zu emittieren, nennt man zwei Photonen Kaskadenübergang. Die emittierten Photonen nennt man verschränkt oder korreliert.
Abbildung 1 Zwei Photonen Kaskadenübergang. Das Quecksilberatom hat 3 Niveaus, wovon das 2. dreifach entartet ist. Beim Übergang vom 3. über das 2. ins erste Niveau werden zwei Photonen emittiert (Wellenlinien), die gleich polarisiert sein müssen, weil sonst der Gesamtdrehimpuls nicht erhalten bliebe. Wie sie polarisiert sind, wird aber erst durch die Messung bestimmt, denn es hängt davon welchen der Wege (über 2a, 2b oder 2c) das Elektron wählt.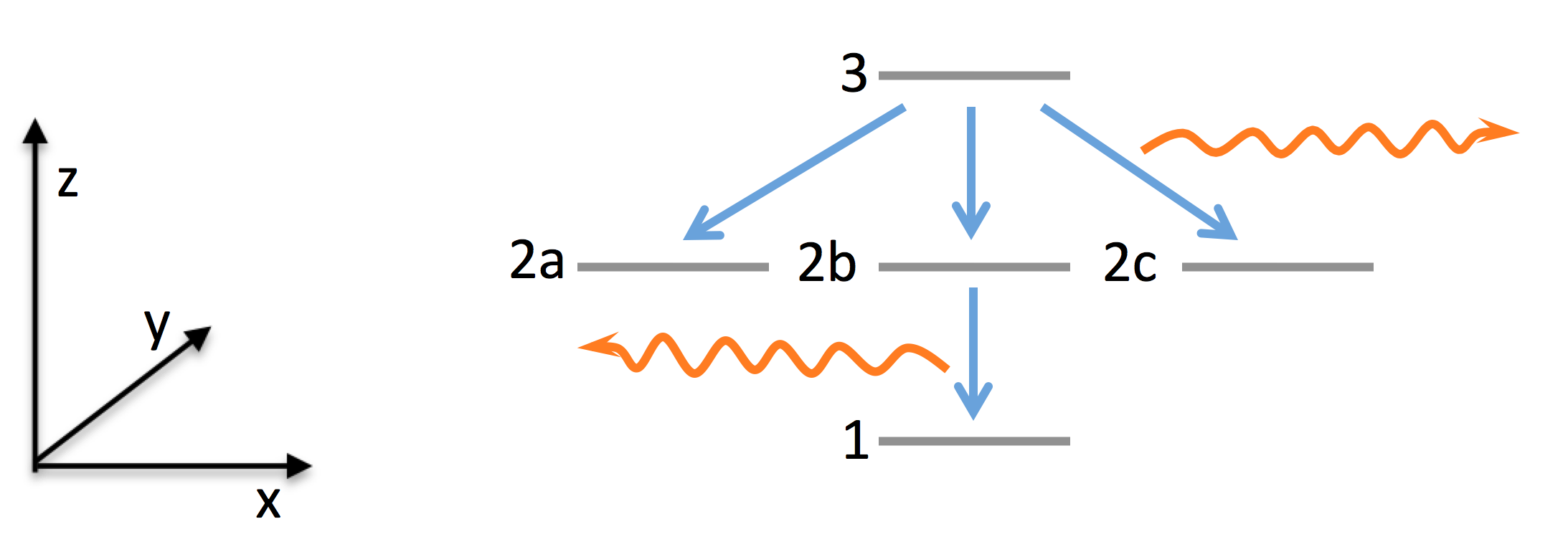
Wie im Doppelspaltexperiment wäre es falsch zu glauben, das herunterfallende Elektron wähle einen der Wege 2a, 2b oder 2c. Vielmehr geht es alle Wege. Die ausgesendeten Photonen sind daher in y- und in z-Richtung polarisiert. Welches davon verwirklicht wird, kann nur durch Messung festgestellt werden. Niels Bohr hätte etwa gesagt: „Es wird erst durch die Messung entschieden. Vorher sind die Photonen in einem Überlagerungszustand beider Polarisationen.“
Jeder mag selber entscheiden, ob er Bohrs Ausdrucksweise folgen will. Unabhängig davon, ob diese Photonen ihre Polarisation tatsächlich haben oder sich erst bei der Messung für eine Richtung entscheiden, sicher ist, dass die Photonen eines solchen Paares sehr eng miteinander verbunden sind, weil sie sozusagen ‘von Geburt auf’ im selben Zustand sind. Wir nennen die Photonen deshalb ‘verschränkt’ oder ‘korreliert’.
2.2. Was bedeutet ‘verschränkt’?
Albert Einstein, Boris Podolsky und Nathan Rosen widersprachen Bohrs Ausdrucksweise aufs heftigste. Sie sagten: Jedes Teilchen hat immer einen Zustand. Wie sich ein Teilchen verhält, ist unabhängig davon, was am anderen, weit entfernten Teilchen geschieht. Sie schlugen dazu das folgende Experiment vor. Man schiesst zwei korrelierte Photonen in entgegengesetzte Richtungen. Dann schickt man die Photonen getrennt durch zwei verschiedene Polarisatoren, an denen je ein Physiker steht, der frei wählen darf, in welche Richtung er seinen Polarisator ausrichtet. Schliesslich misst man an zwei Detektoren, wie häufig und bei welchen Winkeln beide Photonen durch ihren Polarisator hindurch gehen. Das Experiment sieht also etwa so aus:
Abbildung 2 Das Einstein-Podolsky-Rosen Experiment. Ein Quecksilberatom sendet zwei korrelierte Photonen in entgegengesetzter Richtung aus. Mit drehbaren Polarisatoren wird untersucht, wie häufig und bei welchen Winkeln beide Photonen durch ihren Filter hindurch gehen.
Wir haben zwei Polarisatoren, die wir gegeneinander verdrehen können. Den Zwischenwinkel nennen wir wieder a. Statt dass nun aber wie im Experiment zur Polarisation ein Photon durch beide Filter fliegt, schicken wir das eine Photon des Paares durch den einen Filter und das andere durch den anderen.
Dabei stellen wir folgendes fest: Wenn der Zwischenwinkel zwischen den Polarisatoren 0° misst, dann fliegen immer entweder beide Photonen durch ihren Polarisator oder es werden beide absorbiert. Bei 0° kommt es nie vor, dass das eine Photon absorbiert wird, das andere aber durchkommt. Die Polarisatoren können dabei beliebig weit voneinander entfernt stehen, so dass es unmöglich scheint, dass die zwei Photonen noch miteinander ‘sprechen’ können.
2.3. Ein verborgener Plan?
Vielleicht denken Sie jetzt, die Teilchen haben sich vorher abgesprochen und sich gesagt: „Wenn die Polarisatoren senkrecht gerichtet sind oder höchstens zwischen -45° und +45° von der Senkrechten weggedreht sind, gehen wir durch, sonst nicht.“ Die Photonen hätten also sozusagen einen inneren Plan, wie sie sich bei Polarisatoren verhalten (vgl. Abbildung 3).
Abbildung 3 Möglicher Plan für ein Photonenpaar. Jedes Photon weiss für jeden möglichen Polarisator, ob es durchgehen wird oder nicht. Liegt die Achse des Polarisators im grauen Bereich, so geht das Photon hindurch, ist sie im weissen Bereich, so wird es absorbiert.
Im eingezeichneten Beispiel ist der Polarisator 1 um 35°, der Polarisator 2 um -20° gedreht (gestrichelte Linien). Beide Photonen kommen durch den Polarisator hindurch, weil die Achsen der Filter im grauen Bereich liegen.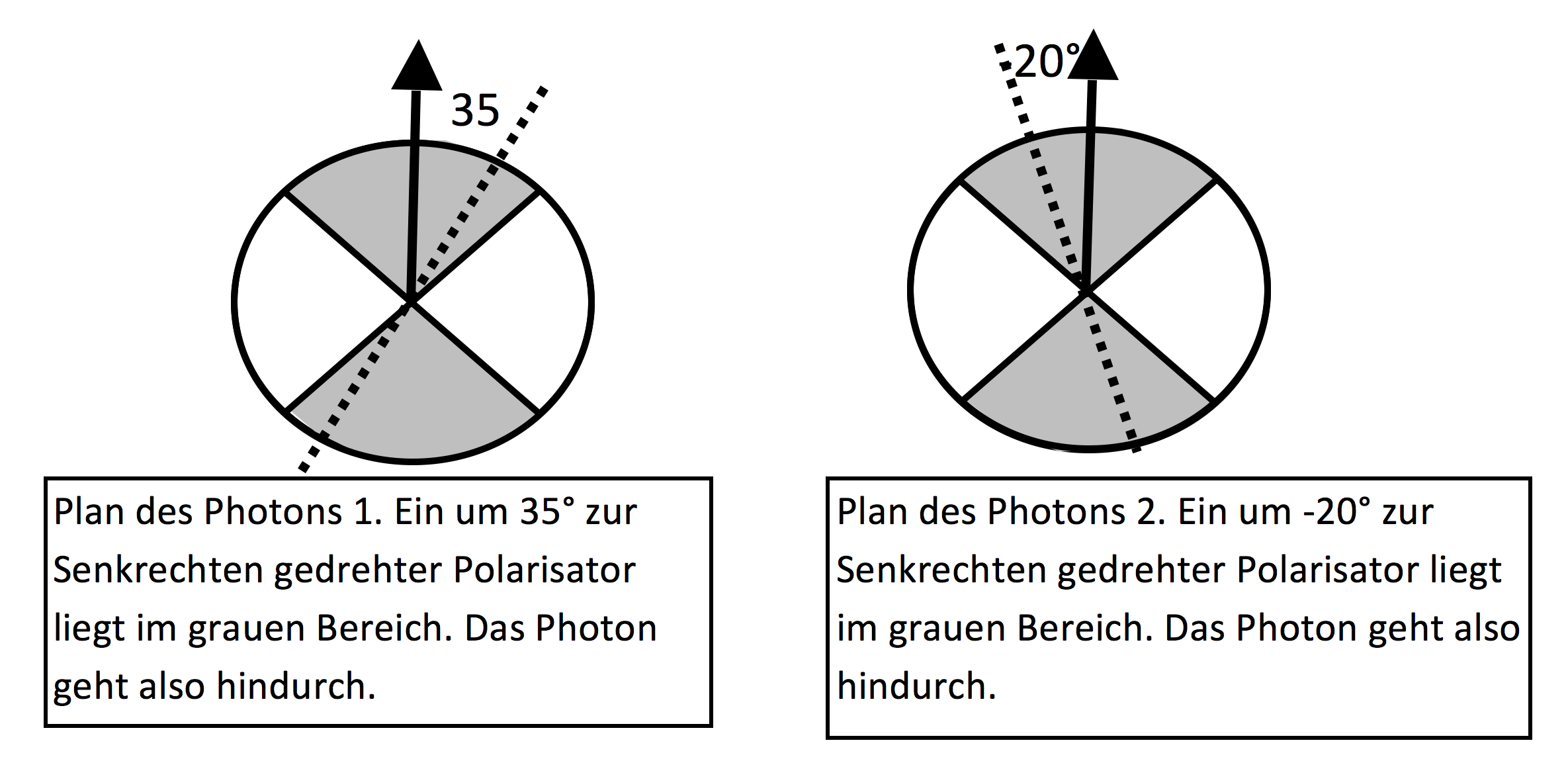
Die Experimente zeigen: Wenn wir beide Polarisatoren gleich richten, gehen immer beide Photonen in den Detektor oder keines von beiden. Wenn wir die Filter senkrecht zueinander einstellen, wird das eine Photon absorbiert, während das andere durch den Filter hindurch geht. Diese beiden Experimente stimmen mit den obigen inneren Plänen völlig überein.
Es sind auch andere ‘Pläne’ denkbar, welche die bisher geschilderten Experimente erklären würden. Damit die Absprache funktionieren kann, müssen sicher drei Bedingungen erfüllt sein:
i. Beide Photonen wissen zu jedem Winkel genau, was sie tun werden. Nur wenn sie sich mit Sicherheit darauf verlassen können, dass das andere Photon sich an einen ausgemachten, fixen Plan hält, können sie bei gleichgerichteten Polarisatoren immer gleich reagieren.
ii. Die Pläne für die beiden Photonen sind für alle Winkel genau gleich.
iii. Der Plan gebietet beiden Photonen, genau in der Hälfte der möglichen Winkel durch ihren Polarisator hindurch zu gehen und in der anderen Hälfte nicht. Denn zu jeder Einstellung des Filters, bei der das Photon hindurch geht, liegt genau senkrecht dazu eine Einstellung, bei der es absorbiert wird.
2.4. Experimente
Welche Resultate bringt das Experiment, wenn wir die Polarisatoren nicht gleich richten oder um genau 90° gegeneinander drehen, sondern um einen beliebigen Winkel a? Theorie und Experimente führen hier zum gleichen Resultat. Es gilt nämlich die gleiche Formel wie für ein einzelnes Photon, das hintereinander zwei Filter durchläuft. In |cos a|2 der Fälle verhalten sich die Photonen genau gleich, d. h. sie gehen beide durch den Filter oder sie werden beide absorbiert.
Wie müssen sich die Photonen absprechen, damit sie das immer schaffen, auch wenn sie nicht im voraus wissen können, wie gewählt wird?
Die Antwort ist: Es gibt überhaupt keine Möglichkeit, dieses Verhalten im voraus abzusprechen. Die Teilchen müssten den Zwischenwinkel zwischen den Polarisatoren kennen, und dazu müssten sie noch während der Messung miteinander kommunizieren.
Betrachten wir einige verschiedene Zwischenwinkel. P sei der Anteil der Paare, bei denen beide Photonen dasselbe tun, also beide in ihren Detektor gelangen oder beide absorbiert werden. Die Photonenpaare zeigen in den Experimenten das folgende Verhalten:
| Winkel a | P = |cos a|2 |
| 0° | 100 % |
| ±30° | 75 % |
| ±60° | 25 % |
| ±90° | 0 % |
Diese Verteilungen werden gemessen, daran gibt’s nichts zu rütteln. Nun nehme ich an, die zwei Photonen hätten einen fixen Plan, der ihnen für jede mögliche Richtung des Polarisators vorschreibt, wie sie sich verhalten sollen. Ich nehme an, die Photonen hätten diesen Plan ausgemacht, als sie gemeinsam produziert wurden. Ich werde zeigen, dass diese Annahme zu einem Widerspruch führt, dass sie also falsch ist.
Beide Photonen verhalten sich immer exakt nach ihrem gemeinsamen Plan. Wenn ich beobachte, wie sich ein Photon an einem Polarisator verhält, dann kenne ich einen Teil des Plans, der auch für das andere Photon gilt. Denn beide Photonen müssen sich ja an denselben Plan halten.
Nun wähle ich für den Polarisator 1 eine feste Achse, die ich 0° nenne, und schaue bei einer Reihe von Photonen, ob sie durch diesen Filter hindurch gehen. Ich drehe den Polarisator 2 um 30° und sehe, dass die Photonen bei 2 in 75 % der Fälle dasselbe tun wie die Photon bei 1. Ich kann also sagen:
Aussage 1: Der Plan bei 30° ist bei 75 % der Photonen gleich wie der Plan bei 0°.
Aussage 2: Der Plan bei -30° ist bei 75 % der Photonen gleich wie der Plan bei 0°.
Aussage 3: Ich stelle den Polarisator 1 auf 30° und den Polarisator 2 auf -30°. Dann liegen 60° zwischen den Richtungen der Polarisatoren. Gemäss Tabelle sind die Pläne für diese Richtungen in 25 % der Fälle gleich.
Es gibt keinen fixen Plan, der die Aussagen 1 bis 3 erfüllt! Denn wenn 75 % der Pläne bei 30° gleich wären wie bei 0° und 75 % der Pläne bei -30° gleich wie bei 0°, dann müssten mindestens 50 % der Pläne bei -30° und bei 30° übereinstimmen.
Mit anderen Worten: Es gibt keinen Plan, der bei Zwischenwinkeln von 30° bei 75 % der Photonen übereinstimmt, bei Zwischenwinkeln von 60° aber nur bei 25 % der Photonen. Damit die Photonen sich so verhalten könnten, müssten sie den Zwischenwinkel zwischen den Polarisatoren kennen. Aber dieser ist zum Zeitpunkt der Messung nicht einmal den Experimentatoren bekannt. Denn jeder Physiker weiss ja nur, wie er seinen Polarisator eingerichtet hat, und nicht, was der andere macht. Jeder nur denkbare fixe Plan zwischen den Photonen führt zu eindeutig anderen Resultaten, als die Experimente sie zeigen. Damit sich die Photonenpaare in den Experimenten so verhalten können, müssen die Photonen noch während der Messung Informationen austauschen können, obwohl sie sich bereits an völlig verschiedenen Orten befinden. So scheint es zumindest.
Der Physiker John Bell, der damals am CERN in Genf tätig war, zeigte mit seiner berühmten ‘Bellschen Ungleichung’ mathematisch, dass eine lokale Erklärung des Einstein-Podolsky-Rosen-Experiments nicht möglich ist. Das Experiment wurde seither mit verschiedenen Teilchenarten durchgeführt und die Vorhersagen der Quantentheoretiker wurden bestätigt (Bre 1).
Das Experiment funktioniert übrigens nicht nur mit der Polarisation von Licht, sondern auch für andere komplementäre Grössen, z. B. für Impuls und Ort oder Energie und Ankunftszeit. Ausserdem können ähnliche Experimente auch mit Materieteilchen durchgeführt werden.
Das No-Cloning-Theorem
Übrigens sieht man mit den Überlegungen zu Abbildung 4 auch, dass der Quantenzustand eines Teilchens nicht kopiert werden kann. Andernfalls könnte man 360 Kopien eines Teilchens herstellen und zu jeder Richtung auf ein Grad genau messen, ob das Teilchen durch den Filter hindurch geht. So könnte ich den Plan -den es ja nicht geben kann- zeichnen. Teilchenzustände können also nicht vervielfältigt werden. Dies nennt man das No-Cloning-Theorem.
2.5. Was ist daran seltsam?
Vielleicht denken Sie jetzt: „Na gut, was soll’s? Dann sendet eben das eine Photon dem anderen eine Nachricht, wie der Polarisator bei ihm gedreht ist.“
So einfach geht das nicht. Wir könnten ja das eine Photon nach New York und das andere nach China schicken. Oder wir könnten sie sogar in verschiedene Galaxien schiessen. Statt die Polarisatoren fest zu montieren, könnten wir sie erst dann drehen, wenn die Photonen schon sehr weit auseinander sind. Solche Experimente mit verzögerter Wahl wurden bereits durchgeführt. Die Photonen oder die Polarisationsfilter müssten mit Überlichtgeschwindigkeit miteinander kommunizieren und scheinen dies auch zu tun. Die Relativitätstheorie sagt aber: Wenn es möglich ist, Informationen mit Überlichtgeschwindigkeit zu verschicken, gibt es auch eine Möglichkeit, Information in die Vergangenheit zu schicken und Botschaften aus der Zukunft zu erhalten.
Leider -oder zum Glück- ist es unmöglich, mit verschränkten Teilchen Botschaften zu senden. Die Teilchen scheinen zwar Informationen auszutauschen, aber wir können dies nur sichtbar machen, wenn wir die Resultate beider Messungen vergleichen. Jeder Experimentator sieht nur ein Teilchen, dass mit einer Wahrscheinlichkeit von 50% durch den Filter hindurch geht.
Es sieht also so aus, als wäre entweder Einsteins Realitätskriterium oder die Lokalität verletzt. Ich habe vorausgesetzt, dass die Winkelverteilung für die Photonen auch dann gilt, wenn ich sie nicht messe. Damit habe ich Einsteins Realitätskriterium vorausgesetzt. Wenn dieses Kriterium gilt, müssen die Photonen sich eine Botschaft zusenden, was der Lokalitätsbedingung widersprechen würde. Deshalb sind die meisten Physiker der Ansicht, entweder sei das Realitätskriterium oder die Lokalitätsbedingung nicht erfüllt. Unter 3.3. werde ich aber zeigen, dass die Viele-Welten-Interpretation lokal-realistisch ist und das EPR-Experiment richtig beschreibt.
3. Interpretation
3.1. Das ist ja nur Statistik!
Man könnte denken, der Einstein-Podolsky-Rosen Effekt sei nur ein statistisches Phänomen. Die Teilchen eines verschränkten Paares seien nicht wirklich miteinander verbunden, sondern nur mit einer gewissen Wahrscheinlichkeit korreliert. Diese Auffassung ist aber falsch. Tatsächlich konnten Greenberger, Horne und Zeilinger zeigen, dass drei verschränkte Teilchen nicht nur statistisch, sondern immer im Widerspruch zum lokalen Realismus steht. Es reicht damit bereits ein einzelnes Experiment, um zu zeigen, dass die drei Teilchen nicht einzeln beschrieben werden können (Zei 1).
3.2. Theorien mit verborgenen Variablen
Einstein, Podolsky und Rosen hofften mit ihrem Gedankenexperiment zu zeigen, dass die Quantentheorie nicht vollständig sei. Sie hofften, dass die Theorie erweitert werden könnte. Vielversprechende Ansätze dazu sind z. B. David Bohms Theorie der Führungswelle oder Arbeiten von Louis de Broglie. Wie ich aber oben gezeigt habe, ist eine Erweiterung zu einer vollständigen, lokal-realistischen Theorie nicht möglich. Die Führungswellen sind nichtlokal oder nicht realistisch.
3.3. Die Viele-Welten-Interpretation
Entgegen der Behauptung vieler Autoren gibt es durchaus eine lokal-realistische Erklärung für das EPR-Experiment, nämlich die Viele-Welten-Interpretation. Offensichtlich erfüllt die Viele-Welten-Interpretation die Lokalitätsbedingung, denn die Schrödingerwelle pflanzt sich immer lokal fort. Und den nichtlokalen Kollaps der Wellenfunktion gibt es nach dieser Interpretation nicht. Sie erfüllt aber auch das Einsteinsche Realitätskriterium. Denn wenn ich den Wert einer physikalischen Größe mit Sicherheit vorhersagen kann, dann gibt es ein Element der physikalischen Realität, das dieser physikalischen Größe entspricht. Nach der Viele-Welten-Interpretation gibt es ja nicht nur die messbaren und vorhergesagten Elemente, sondern überhaupt alles, was von der Schrödingerfunktion beschrieben wird.
Was ist im EPR Argument schief gelaufen? – Erstens gehen EPR stillschweigend davon aus, ein Teilchen könne sich nur in einem Zustand befinden. Charakteristisch für die Quantentheorie ist aber gerade, dass sich ein Teilchen nie nur in einem bestimmten Zustand befindet. Wenn zwei Zustände a und b möglich sind, dann befindet sich ein Teilchen fast nie ausschliesslich im einen oder im anderen Zustand. Im Gegenteil: Das Teilchen kann dann nicht nur im Zustand a oder b gefunden werden, sondern auch in einer beliebigen Überlagerung dieser Zustände.
Zweitens haben EPR implizit angenommen, dass sich der Beobachter nicht verändere. Dies ist aber schon in der klassischen Physik eine fragwürdige Annahme.
Nach der Viele-Welten-Interpretation sieht der Ablauf des Experimentes etwa so aus (Abbildung 5). Vor dem Experiment sind aus Sicht des Beobachters A alle experimentellen Resultate möglich. Das Photon bei A kann in jede Richtung polarisiert sein. Alle diese Möglichkeiten sind real, denn sie alle sind nötig für eine vollständige Beschreibung des Experimentes. (Hier verwende ich nicht Einsteins Begriff real, sondern den, den ich im Artikel Viele-Welten-Interpretation eingeführt habe: Wenn wir ein mathematisches Element zur Berechnung eines Experimentes zwingend brauchen, so existiert in der Natur ein Äquivalent zu diesem Element. Ein solches Element nenne ich real. Diese Definition ist aber durchaus in EPRs Sinn, denn diese zielten ja gerade auf verborgene Variablen, die zwar nicht messbar, aber dennoch real sein sollten.)
Zu jeder möglichen Welt des Beobachters A gehört ein Beobachter B. Die Beobachter B sind nicht alle gleich. Denn jeder von ihnen hat ein Photon, das mit demjenigen Photon bei A verschränkt ist, das zu seiner Welt gehört.
Noch einmal für alle, die diese Beschreibung für aufwändig und exotisch halten: Das ist die Beschreibung der Quantentheorie, die die Physiker täglich verwenden. Die Theorie ist extrem präzise und erfolgreich und kaum ein Physiker erwartet, dass sie noch wesentlich vereinfacht werden könnte.
Abbildung 5 Vor der Messung existieren für A verschiedene Welten (sechs davon sind gezeichnet). Alle diese Welten sind gleichermassen real. A muss sich nun entscheiden, wie er die Polarisationsfilter stellt. Mit diesem Entscheid entscheidet er sich auch für eine Welt (gelb markiert).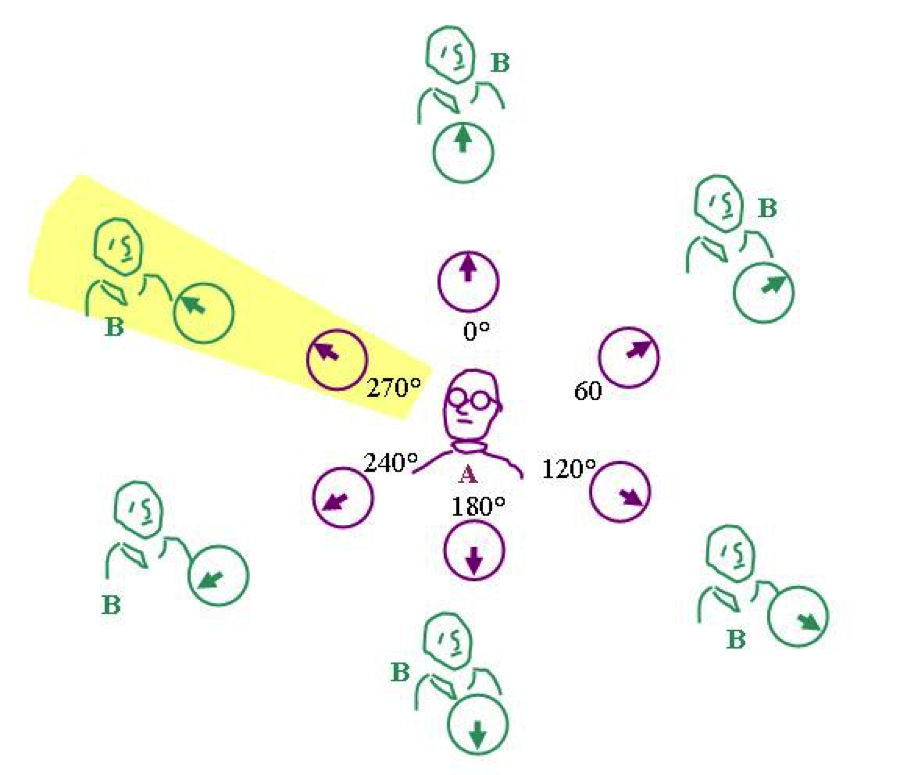
Nachdem A seinen Polarisationsfilter eingestellt hat, hat er sich für eine Welt entschieden. Durch diesen Entscheid sendet er nicht eine mysteriöse Nachricht zu B, sondern er blickt einfach von nun an nur noch in diese Welt, in welcher der Polarisationsfilter bei A auf 270° ist. Es gibt also keine nichtlokale Veränderung der Welt, sondern A dreht sich ganz lokal und blickt (im Hilbertraum) in eine andere Richtung. Auch dies ist keine Ad-hoc Annahme, sondern ganz einfach das, was die Quantentheorie beschreibt. Wer mit dieser Beschreibung nicht glücklich ist, muss die Quantentheorie ändern.
Abbildung 6 Bei seiner Messung spaltet sich A in die verschiedenen Welten auf. Er erlebt nur seine Möglichkeit, in der er ein Beobachter ist, der die Polarisation bei 270° gemessen hat.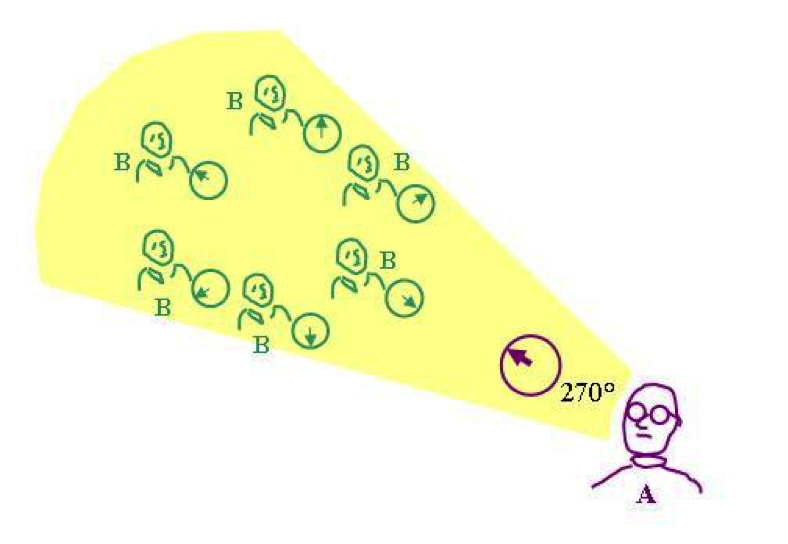
Erst kommt Einsteins Realitätskriterium ins Spiel. Wenn bei A bei 270° das Photon durch den Polarisationsfilter geht, dann kann A mit Sicherheit den Wert bei B voraussagen, wenn B seinen Filter auch auf 270° stellt oder senkrecht dazu. Das Einsteinsche Realitätskriterium fordert nun:
“Kann man den Wert einer physikalischen Größe mit Sicherheit vorhersagen, dann gibt es ein Element der physikalischen Realität, das dieser physikalischen Größe entspricht.”
Das Realitätskriterium fordert also, dass es bei B ein Photon gibt, das ebenfalls bei 270° durch den Filter gehen würde. Selbstverständlich ist dies in der Viele-Welten-Interpretation erfüllt. Denn nach dieser Interpretation existieren ja alle Photonen, die überhaupt nur möglich sind.
4. Zusammenfassung
Einstein, Podolsky und Rosen (EPR) wollten mit einem Gedankenexperiment zeigen, dass die Quantentheorie unvollständig sei. Nach dem oben Gesagten erscheint ihre Argumentation als Schildbürgerei: Von der Beschreibung der Quantentheorie wird mehr oder weniger willkürlich ein Teil für nicht existent erklärt, weil er nicht mehr beobachtet werden könne. Danach weist man mit einer raffinierten Überlegung nach, dass das verbleibende Fragment der Quantentheorie nicht mehr vollständig ist.
Nach der Viele-Welten-Interpretation ist die Quantentheorie erstens vollständig. Zweitens aber beweist das EPR-Experiment, dass aus der Theorie auch nicht ohne weiteres Dinge weggelassen werden können. Die Wellenfunktionen müssen als real angesehen werden, sonst fehlt der Beschreibung etwas.
Die Viele-Welten-Interpretation ist eine lokal-realistische Theorie, die das EPR-Experiment korrekt erklärt. Obwohl dies gemäss vielen Lehrbüchern unmöglich ist.
Viele Physiker finden, die Viele-Welten Interpretation erkläre überhaupt nichts. Aber mit der Viele-Welten Interpretation verschwindet jede Problematik aus dem EPR Experiment. Das EPR Experiment, über das die philosophisch interessierten Physiker seit Jahrzehnten verzweifelt grübeln, wird degradiert zu einem einfachen klassischen Experiment. Man stelle sich das folgende Experiment vor: Ein Physiker steht vor sechs Türen verschiedener Farbe, von denen er eine wählen soll. Sobald er aber eine Türe öffnet, werden die anderen fünf unwiederruflich verriegelt. Hinter der geöffneten Türe findet der Physiker einen langen Gang und an dessen Ende eine Türe der gleichen Farbe, wie die der geöffneten Türe (Abbildung 7). Der Physiker kann das Experiment in mehreren ähnlich gebauten Gebäuden wiederholen und immer stimmt die Farbe der zweiten Türe mit derjenigen der ersten überein.
Abbildung 7 Ein Physiker soll eine von sechs verschieden gefärbten Türen wählen. Nach seiner Wahl werden die anderen fünf Türen für immer blockiert. Hinter der geöffneten Türe findet der Physiker einen Gang und schliesslich eine weitere Türe der eben gewählten Farbe.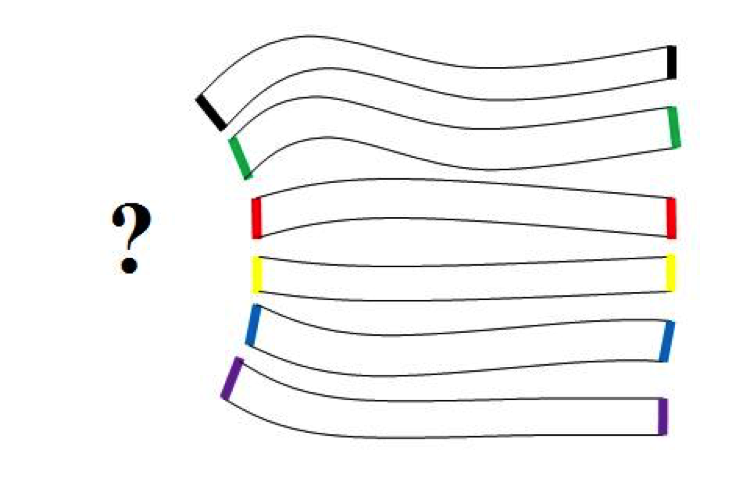
“Die Welt hinter den Türen ist lediglich als Möglichkeit vorhanden. Bevor der Physiker eine Türe geöffnet hat, darf er nicht sagen, dahinter liege ein realer Gang. Wenn der Physiker eine Türe wählt, kollabieren die anderen fünf Möglichkeiten. Das grosse Rätsel der Quantentheorie ist: Wie kann die zweite, weit entfernte Türe wissen, welche Farbe sie haben muss? Der Physiker hat diese Türe überhaupt nicht berührt! Das Experiment zeigt eine nichtlokale Kausalität: Der bewusste Entscheid des Physikers verändert die Farbe der Türe an einem völlig anderen Ort!”
Nach der Viele-Welten-Interpretation sind da einfach sechs verschiedene Gänge, und die Türe am Eingang hat immer die gleiche Farbe wie die am Ausgang. Zwar kann jeweils nur ein Gang beobachtet werden, aber die anderen existieren trotzdem. Die anderen Gänge sind auch in der Beschreibung der Quantentheorie enthalten, nämlich in der Wellenfunktion. Die ganze Verwirrung entsteht erst, wenn wir annehmen, dass die Wellenfunktion nicht die Realität beschreibt, sondern nur ein mathematischer Trick ist.
5. Weiterführende Artikel auf dieser Homepage
Viele-Welten-Interpretation
Quantenradierer
Sind Dinge, die niemand beobachtet, real?
23.03.2014
 Was hat Quantenphysik mit Telepathie zu tun? Wehrli (Vorstandsmitglied) geht in seinem Vortrag an der Generalversammlung der Skeptiker Schweiz auf pseudowissenschaftliche Behauptungen von sogenannten “Telepathen” und ähnlichen Menschen ein.
Was hat Quantenphysik mit Telepathie zu tun? Wehrli (Vorstandsmitglied) geht in seinem Vortrag an der Generalversammlung der Skeptiker Schweiz auf pseudowissenschaftliche Behauptungen von sogenannten “Telepathen” und ähnlichen Menschen ein.
6. Weiterführende Bücher:
Philip Wehrli, ‘Das Universum, das Ich und der liebe Gott’, (2017), Nibe Verlag,

In diesem Buch präsentiere ich einen Gesamtüberblick über mein Weltbild: Wie ist das Universum entstanden? Wie ist das Leben auf der Erde entstanden? Was ist Bewusstsein und woher kommt es? Braucht es dazu einen Gott?
Viele Artikel dieses Blogs werden in diesem Buch in einen einheitlichen Rahmen gebracht, so dass sich ein (ziemlich) vollständiges Weltbild ergibt.
Leserunde bei Lovelybooks zum Buch ‘Das Universum, das Ich und der liebe Gott’, von Philipp Wehrli (abgeschlossen)
Rezensionen bei Lovelybooks
Rezensionen bei Amazon
Film-Präsentation zum Buch
Nibe Verlag
Rae Alastair, ‘Quantenphysik: Illusion oder Realität?’, (1996), Reclam
Vielleicht die einfachste Erklärung zum Einstein-Podolsky-Rosen Experiment, die ich kenne.
Selleri Franco, (1990) ‘Die Debatte um die Quantentheorie’, Vieweg, Braunschweig
Sellerie zeigt die Interpretationsprobleme, die durch die Quantentheorie aufgeworfen wurden und erklärt, wie sie von den Begründern der Theorie gelöst wurden und wie die Interpretationen heute z. T. mit Experimenten überprüft werden können. Dabei verwendet er ziemlich abstrakte Mathematik. Man kann zwar über die meisten Formeln hinweglesen, aber das Buch verliert dabei natürlich etwas.
Spektrum Akademischer Verlag, Heidelberg, ‘Quantenphilosophie – Reihe Verständliche Forschung’, Neuser / Neuser-von Oettingen (Herausgegeber)
Wer sich für die Philosophie hinter der Quantentheorie interessiert, findet hier ein breites Spektrum anregender Artikel, unter anderem von Schrödinger, Gamov, d´Espagnat, Cassidy und de Witt. Die Artikel sind kurz, prägnant und allgemeinverständlich und werden mit vielen schönen Grafiken illustriert.
Zeilinger Anton, ‘Einsteins Spuk – Teleportation und weitere Mysterien der Quantenphysik’
Eine auch für Nicht-Wissenschafter nachvollzierbare, lebendig geschriebene Schilderung der EPR Experimente und der Quantenteleportation von dem Physiker, der die Experimente selber durchgeführt hat.

