Spin 1/2 Teilchen drehen

Visits: 1819

Philipp Wehrli, 2. Januar 2002

Wenn Dinge gedreht werden, sind sie spätestens nach einer Drehung um 360° wieder gleich -würde man denken. Teilchen mit Spin 1/2 unterscheiden sich nach einer Drehung um 360° von solchen, die nicht gedreht wurden. Erst nach einer Drehung um 720° sind sie wieder gleich. Wie dies im Experiment aussieht, wird hier beschrieben.

Abbildung 1

a) Der König sieht nach einer Drehung um 180° wieder gleich aus. Das entspricht einem Spin 2.

b) Die Sieben braucht eine Drehung von 360°, um wieder gleich auszusehen. Sie hat Spin 1.

c) Ein Teilchen mit Spin 1/2 ist erst nach einer Drehung 720° wieder im gleichen Zustand.

Was wird gedreht?

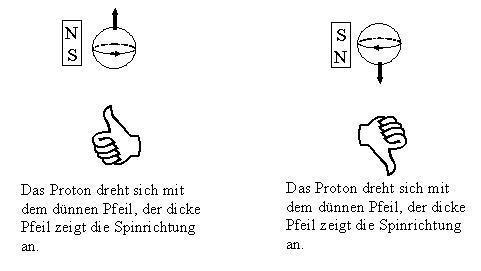
In diesem Experiment drehen wir ein Neutron, also ein Teilchen, das wie das Proton oder das Elektron Spin ½ hat. Drehen kann man nur Dinge, die nicht völlig symmetrisch sind. Wie erkennen wir, ob das Neutron gedreht wurde? -Neutronen sind zwar elektrisch neutral, sie sind aber aus drei geladenen Quarks zusammengesetzt und haben deshalb wie das Proton ein magnetisches Moment. Ausserdem drehen sie sich um sich selber, sie haben einen Spin. Die Richtung dieser Drehung wird durch einen Vektor (einen Pfeil) beschrieben, den man mit Hilfe der ‘Rechten-Hand-Regel’ findet: Wenn man die Finger der rechten Hand so krümmt, dass sie die Richtung der Drehung anzeigen, dann zeigt der Daumen in die Richtung des Spins. Gedreht wird die Richtung dieses Pfeils.

Abbildung 2

Wie wird gedreht?

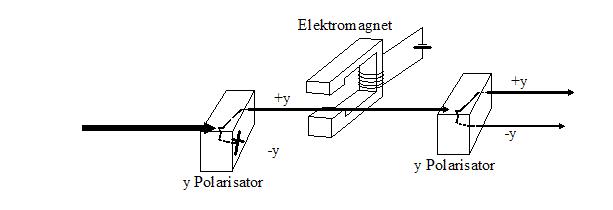
Wir drehen nun die Spinrichtung der Neutronen. Damit wir die Drehung auch erkennen können, beginnen wir mit einem Strahl von Neutronen, die alle die gleiche Spinrichtung haben. Wir erreichen dies, indem wir die Neutronen durch einen y Polarisator schicken. So erhalten wir zwei Teilstrahle, einen mit positivem und einen mit negativem Spin. Wir wählen den Strahl +y, so dass wir einen reinen Strahl mit schön ausgerichteten Neutronen haben.

Gedreht werden die Neutronen in einem homogenen Magnetfeld. Anders als im Polarisator sind im homogenen Magnetfeld die Feldlinien überall gleich dicht. Der Strahl wird daher nicht in weitere Strahlen aufgeteilt. Aber die Neutronen, die wir als kleine, sich drehende Magnete ansehen können, beginnen zu präzedieren, d. h. die Spinrichtung ändert sich langsam und stetig.

Woran sehen wir, dass die Teilchen gedreht werden?

Die Drehung können wir sichtbar machen, indem wir den Neutronenstrahl mit einem zweiten y Polarisator analysieren. Ohne das äussere Magnetfeld müssten alle Neutronen auch im zweiten Polarisator Spin +y zeigen. Je länger die Neutronen aber dem Magnetfeld ausgesetzt sind oder je stärker das Feld eingeschaltet wird, desto mehr Neutronen erscheinen mit Spin -y. Befinden sich die Neutronen eine bestimmte Zeit im Magnetfeld, dann haben sie alle ihren Spin gerade umgekehrt. Lassen wir sie noch länger im Magnetfeld, so drehen sie sich weiter, bis alle wieder positiven Spin haben. Wir haben die Neutronen also einmal um sich selber gedreht. Den gedrehten Neutronen sieht man überhaupt nichts Besonderes an. Sie haben sich um 360° gedreht und sind genauso die alten, wie eine Rosen 7 die alte bleibt, wenn man sie um 360° dreht.

Abbildung 3

Eine andere Methode, festzustellen, wie weit sich der Spin gedreht hat, gibt es z. B. bei Myonen. Diese zerfallen im Durchschnitt nach etwa 2.2 Mikrosekunden in ein Elektron, ein Neutrino und ein Antineutrino. Die Elektronen werden bei hohen Energien vorzugsweise in die Richtung emittiert, die der Spinrichtung des Myons entgegengesetzt ist. So können wir sehr genau feststellen, wie schnell die Myonen im Magnetfeld präzessieren, also gedreht werden.

Woran sehen wir, dass die Teilchen sich bei einer Drehung um 360° verändern?

Elementarteilchen können nicht einfach als Teilchen angeschaut werden. Vielmehr bewegen sie sich wellenartig. Die Höhe (Amplitude) der Welle bestimmt, mit welcher Wahrscheinlichkeit ein Teilchen in einem bestimmten Zustand beobachtet wird. Wird ein Teilchen um sich selber gedreht, so verschiebt sich die Phase dieser Welle gegenüber der Phase eines ruhenden Teilchens. Die Höhe der Welle bleibt gleich hoch, deshalb ändert sich auch nichts an der Wahrscheinlichkeit, das Teilchen zu sehen. Ein einzelnes Teilchen, das um 360° gedreht wird, sieht genau gleich aus wie ein einzelnes ungedrehtes. Wir können aber sichtbar machen, dass die Phase der Wahrscheinlichkeitswelle sich verschiebt.

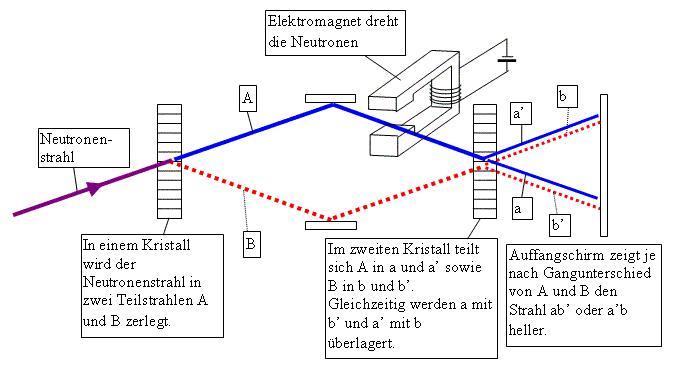
Dazu zerlegen wir die Welle eines einzelnen Neutrons mit einem ersten Strahlteiler in zwei Teilwellen A und B. Ein Strahlteiler ist einfach ein Kristall, der die Hälfte der Neutronen gerade durchlässt und die anderen mit einem Knick ablenkt. Wenn nicht gemessen wird, ob ein Neutron geradeaus fliegt oder geknickt wird, so geht es wie beim Doppelspaltversuch beide Wege. Die Teilstrahlen A und B werden umgelenkt und in einem zweiten Strahlteiler wieder miteinander gekreuzt und dabei überlagert, also zur Interferenz gebracht. D.h.: beiden Strahlen werden erstens noch einmal geteilt in a und a’ bzw. b und b’, und danach wird a mit b’ überlagert, sowie a’ mit b.

Abbildung 4

Wenn die Wege von A und B nicht ganz genau gleich lang sind, kann es geschehen, dass z. B. a’ gerade dort seine Wellenbuckel hat, wo bei b die Täler sind. Die Strahlen a’ und b würden sich gerade gegenseitig auslöschen. Weil keine Teilchen verloren gehen können, wäre dann der Strahl ab’ dafür umso stärker. Die Wege von A und B sollen am Anfang so justiert werden, dass der Strahl ab’ maximal ist, während sich die Teilstrahlen a’ und b gegenseitig auslöschen.

Nachdem wir dies erreicht haben, drehen wir das Neutron im einen Teilstrahl A, ohne seinen Weg zu verlängern. Dazu wird senkrecht zu A ein Magnetfeld angelegt, so dass das Neutron um die Richtung des Magnetfeldes gedreht werden. Obwohl das Neutron ungehindert weiterfliegt, verschieben sich bei der Drehung die Wellenbuckel im Teilstrahl A (bzw. a und a’), während sie im Teilstrahl B (bzw. b und b’) gleich bleiben. Werden die beiden Teilstrahlen überlagert, so wird der Gangunterschied plötzlich sichtbar. Je nach Gangunterschied verändern sich die Intensitäten der Strahlen ab’ und a’b.

Hinter dem zweiten Strahlteiler tritt ein Interferenzmuster auf, das davon abhängt, wie weit die Neutronen gedreht werden. Interessanterweise ist das Interferenzmuster anders, wenn die Neutronen um 360° gedreht werden, als wenn sie nicht oder um 720° gedreht werden. Da an den Weglängen der Strahlen nichts geändert wird, kann dies nur an der Drehung liegen (Aud 1).

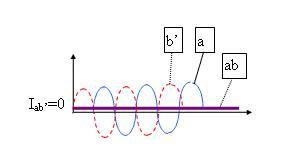
Abbildung 5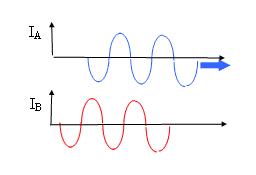Wenn die Neutronen in einem Strahl gedreht werden, verschiebt sich ihre Welle gegenüber einer Welle von ungedrehten Teilchen. Wir sehen aber nur die Amplitude der Quantenwellen, also die Höhe der Wellenbuckel, und weil die Amplitude

I^A (der gedrehten Neutronen) gleich bleibt wie die Amplitude I^B (der ungedrehten Neutronen), sehen wir nichts von der Verschiebung.

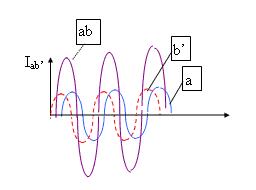
Werden aber zwei Teilstrahlen, zum Beispiel a und b’ überlagert (gestrichelte Welle), so ergibt sich je nach Gangunterschied eine höhere oder eine kleinere Amplitude I^ab’

Wenn die Überlagerung der Teilwellen a und b’ ohne Magnetfeld eine maximale Amplitude ergibt, so löschen sie sich gerade aus, wenn die Neutronen im Strahl A, also in a und a’ um 360° gedreht werden. Eine Drehung um 360° verändert also etwas an den Neutronen.

Interpretation des Experimentes

Kann ich mir anschaulich vorstellen, was die Neutronen hier tun? Es gibt in unserem Alltag tatsächlich einige Analogien, die aber alle ein bisschen hinken. Ich finde sie trotzdem ganz anregend.

1.) Nehmen Sie einen Papierstreifen, verdrehen Sie ihn um 180° und kleben Sie ihn dann zu einer Schleife zusammen. Diese Konstruktion nennt man Möbiusband.

Abbildung 6. Möbiusband von M. C. Escher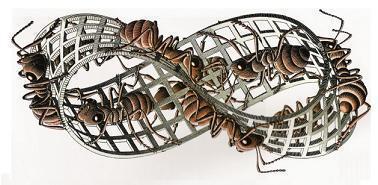

Wenn eine Ameise auf einem Möbiusband läuft, muss sie zweimal im Kreis herumgehen, bis sie wieder an derselben Stelle ist. Vielleicht ist ja der Raum irgendwie möbiusartig verdreht?

2.) Nehmen Sie eine gefüllte Kaffekanne in Ihre rechte Hand. Versuchen Sie nun, diese Kanne einmal um sich selber zu drehen, während Sie mit den Füssen am Boden stehen bleiben. Es ist dazu eine ziemlich komplizierte Bewegung nötig, und Sie werden die Kanne zweimal drehen müssen, bis alles wieder so ist, wie es einmal war. Achtung, Kaffee nicht verschütten und besser nicht zu sehr füllen!

3.) Eine Drehung ist eine beschleunigte Bewegung. Vielleicht wird das Neutron bei der Drehung durchgeschüttelt und verändert sich deshalb. Wenn man zum Beispiel ein weiches Ei dreht, hinkt das Innere im Ei nach. Vielleicht hat das Neutron ja auch ein ‘Inneres’ das nachhinkt. Bemerkenswerterweise verhält sich aber die Spinamplitude zumindest rechnerisch genau gleich, wenn nicht das Neutron, sondern der Apparat um das Neutron herum gedreht wird. Ein entsprechendes Experiment hat Kuyatt (Kuy 1) durchgeführt.

Allerdings kann man dann die Veränderung der Neutronen nicht so schön am Interferenzbild sehen. Es erfordert eine ziemlich knifflige mathematische Analyse, um zu sehen, dass sich bei der Drehung um 360° die Amplitude verändert (Fey 1).

 

Weiterführende Bücher:

Audretsch Jürgen / Mainzer Klaus (Hrsg), ‘Wieviele Leben hat Schrödingers Katze?’, Spektrum Akademischer Verlag, (1990), Heidelberg / Berlin / Oxford
Verschiedene Autoren interpretieren die Quantentheorie anhand der aktuellen Experimente. Sehr anregend. Die entscheidenden Argumente sind aber nur nachvollziehbar, wenn man die Quantentheorie schon kennt und vor mathematischen Formeln nicht zurückschreckt.
Das obige Experiment wird im Beitrag von Anton Zeilinger beschrieben.

Feynman / Leighton / Sands, ‘Feynman Vorlesungen über Physik, Band III: Quantenmechanik’, (1988), Ouldenbourg, München / Wien
Wer Physik studiert, kennt und schätzt Feynman. Sehr ausführlich, aber auch sehr originell und didaktisch geschickt erklärt der Nobelpreisträger die Quantenmechanik. Das Buch ist das Vorlesungsskript für die Grundvorlesung und setzt demgemäss ein wenig Mathematik voraus. Feynman zeigt, wie man mit Spins rechnet und rechnet das obige Beispiel vor.

Spektrum Akademischer Verlag, Heidelberg, ‘Quantenphilosophie – Reihe Verständliche Forschung’, Neuser / Neuser-von Oettingen (Herausgegeber)
Wer sich für die Philosophie hinter der Quantentheorie interessiert, findet hier ein breites Spektrum anregender Artikel, unter anderem von Schrödinger, Gamov, d´Espagnat, Cassidy und de Witt. Die Artikel sind kurz, prägnant und allgemeinverständlich und werden mit vielen schönen Grafiken illustriert.

Spektrum Akademischer Verlag, (1995), Heidelberg, ‘Teilchen, Felder und Symmetrien – Reihe Verständliche Forschung’
Eine Reihe anregender Artikel zum Thema Teilchenphysik, ideal als Einstieg. Die Artikel sind kurz, prägnant und allgemeinverständlich und werden mit vielen schönen Grafiken illustriert.