Visits: 1596
Philipp Wehrli, 2. Januar 2002
Nach der allgemeinen Relativitätstheorie ist die Gravitation nicht mehr eine Kraft, sondern ein Effekt, der durch die Krümmung der Raumzeit entsteht. Was Krümmung der Raumzeit bedeutet und wie sie bewirkt, dass sich zwei Massen anziehen, versuche ich hier einsichtig zu machen. Dieser Artikel setzt die spezielle Relativitätstheorie und die ausgewählten Effekte zur allgemeinen Relativitätstheorie voraus.
1. Einleitung
2. Raum-Zeit-Diagramme
3. Die gekrümmte Raum-Zeit
4. Gravitationsbeschleunigung
5. Newtons Gravitationsgesetz als erste Näherung
6. Die allgemeine Relativitätstheorie aus Sicht des Poeten
7. Weitere Artikel zu ähnlichen Themen
8. Weiterführende Bücher
9. Externer Link
1. Einleitung
Ich habe bereits in Effekte der ART beschrieben, wie Licht zu einer Masse hin gebogen wird, weil in der Nähe der Masse die Zeit langsamer läuft. Tatsächlich wird im Rahmen der allgemeinen Relativitätstheorie jede Art von Gravitationskraft als eine Folge der Krümmung der Raum-Zeit beschrieben. Weil die Zeit in der Nähe einer Masse langsamer geht, fallen Steine zu Boden. Wie dies funktioniert, will ich auf dieser Seite kurz andeuten.
Ich stelle hier zwei Sichtweisen von gekrümmten Räumen vor. Die Idee zur ersten Sichtweise stammt im Wesentlichen von Lewis Epstein (Eps 1). Sie zeigt, wie durch die Krümmung der Raumzeit die Gravitation entsteht. In der zweiten Sichtweise zeichne ich die Koordinatensysteme nicht gekrümmt, sondern ich nehme an, dass in der Nähe von Massen die Bewegung durch die Raumzeit verlangsamt ist. Durch diese Verlangsamung der Bewegung werden die Teilchen abgelenkt. Ich zeige rechnerisch, dass diese Ablenkung im dreidimensionalen Raum genau der bekannten Gravitationsbeschleunigung entspricht.
Für tiefer gehende Fragen reicht diese Darstellung allerdings nicht. Dazu müsste man sich eingehend mit der Geometrie gekrümmter Räume auseinandersetzen (Olo 1).
2. Raum-Zeit-Diagramme
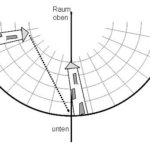
Ich verwende auch hier die ungewöhnlichen Raumzeit-Diagramme, die ich in der speziellen Relativitätstheorie eingeführt habe. Ich wähle einen Beobachter, der den Überblick über das Geschehen hat und in regelmässigen Abständen in ein Diagramm den Aufenthaltsort und die angezeigte Eigenzeit aller Uhren einträgt. Die Uhren scheinen sich mit konstanter Geschwindigkeit c durch die Raumzeit in diesem Diagramm zu bewegen. Verschiedene Uhren laufen nicht unbedingt gleich schnell, sie haben also nicht alle die gleiche Eigenzeitkoordinate.
Abbildung 1 In der speziellen Relativitätstheorie ist die Raumzeit flach, das heisst, die Knotenpunkte im Koordinatensystem haben immer den gleichen Abstand. Man könnte sagen, die Uhren bewegen sich mit Lichtgeschwindigkeit durch die Raumzeit. Je weiter der Weg, den eine Uhr zurücklegt (y-Achse), desto kleiner ist ihre Eigenzeit (x-Achse). Im hier gezeichneten Diagramm haben alle Uhren konstante Geschwindigkeit. Die vom ausgewählten Beobachter eingetragenen Punkte liegen deshalb immer auf Kreisen.
3. Die gekrümmte Raum-Zeit
Auf der Seite Effekte der allgemeinen Relativitätstheorie habe ich erwähnt, dass Uhren langsamer laufen, wenn sie sich in der Nähe einer Masse befinden. Wie muss nun das Raum-Zeit-Diagramm verändert werden, wenn die Zeit nicht überall gleich schnell läuft?
Wieder stelle ich mir einen auserwählten Beobachter vor, der in regelmässigen Zeitabständen (nach seiner Uhr) in ein Diagramm den Aufenthaltsort und die Eigenzeit aller Uhren einträgt. Ich möchte das Diagramm wieder so machen, dass die so eingetragenen Punkte gleichmässige Abstände voneinander haben. Bei der Erstellung des Diagramms würde es also aussehen, als würden sich die Spuren aller Uhren im Diagramm gleich schnell ausbreiten.
Wir haben gesehen, dass die Zeit unten langsamer läuft als oben. Ich zeichne deshalb die Zeiteinheiten unten weiter auseinander als oben. Weil sich die Spuren aller Uhren gleich schnell ausbreiten, dauert es dann für die untere Uhr länger, bis eine Zeiteinheit vergangen ist. Wenn ich Zeiteinheiten unten dehne, verbiegen sich die Zeitachsen zu Kreisen. Dies ist gemeint, wenn von Krümmung der Raumzeit gesprochen wird.
Beachte, dass Abbildung 2 nur eine Raumdimension zeigt, nämlich die senkrechte Linie auf die Masse zu.
Abbildung 2 Diagramm einer gekrümmten Raum-Zeit.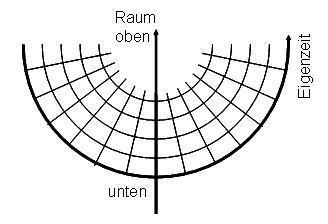
Wie sieht nun die Uhrenverlangsamung in diesem Raum-Zeit-Diagramm aus?
Die Bilder der Uhren bewegen sich im Diagramm gleich schnell, die Linien in Abbildung 4, welche die verschiedenen Wege der Uhren durch die Raumzeit zeigen, sind also immer gleich lang. Dennoch geht die obere Uhr bei ihrer Rückkehr vor, weil die Zeit oben schneller vergeht.
Abbildung 3 Ein gekrümmtes Raum-Zeit-Diagramm. Wenn ein aussenstehender Beobachter Aufenthaltsort und Eigenzeit von zwei Uhren in regelmässigen Zeitabständen (nach seiner eigenen Uhr) in ein Diagramm eintragen würde, so würden sich die Spuren der zwei Uhren gleich schnell im Raumzeitdiagramm ausbreiten. Weil die Eigenzeitachse unten gedehnt ist, geht die obere Uhr nach einiger Zeit vor. Obwohl die eine Uhr erst 6 Uhr zeigt, die andere aber 11 Uhr, kehren die Uhren gleichzeitig zur Mitte des Turmes zurück, nämlich genau nach elf Eintragungen des externen Beobachters. Das sieht man im Diagramm daran, dass die grüne und die rote Spur bei der Rückkehr gleich lang sind.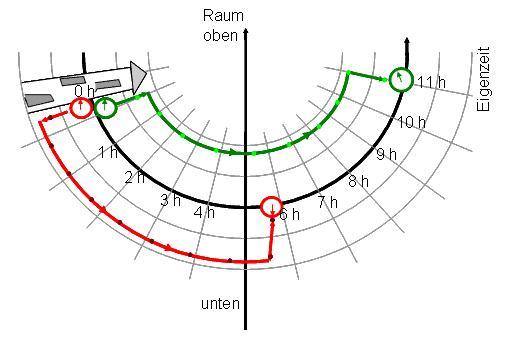
4. Gravitationsbeschleunigung
Wie kommt nun die Gravitationsbeschleunigung zu Stande? In der flachen Raumzeit werden die unbeschleunigten Körper durch Geraden beschrieben. In der gekrümmten Raumzeit ändert sich daran nichts, wenn wir die Krümmung wie oben beschrieben darstellen. Teilchen auf die keine Kräfte wirken, bewegen sich geradeaus.
In der flachen Raum-Zeit entspricht einem ruhenden Körper eine Parallele zur Zeitachse. Im Diagramm der gekrümmten Raum-Zeit gibt es keine solche Parallele, weil die Zeitachse ja gekrümmt ist. Halten wir einen Ball auf dem Dach des Turmes in Ruhe, so wird der Ball wie die obere Uhr in Abbildung 4durch eine gekrümmte Linie dargestellt. Die Linie ist gekrümmt, weil ich Kraft brauche, um den Ball zu halten.
Sobald ich den Ball loslasse, wirkt keine Kraft mehr und der Ball bewegt sich auf einer Geraden im Raum-Zeit-Diagramm. In der gekrümmten Raum-Zeit nennt man solche ‘Geraden’ ‘Geodäten’.
Abbildung 4 In der gekrümmten Raumzeit fallen die Körper dorthin, wo die Zeit am langsamsten läuft. Körper, auf die keine Kräfte wirken, bewegen sich auf Geraden (Geodäten). Die Gravitation ist nach der allgemeinen Relativitätstheorie keine Kraft wie z. B. die elektromagnetische Kraft. Das Herunterfallen geschieht nur, weil die Raumzeit gekrümmt ist, nicht weil eine Kraft wirkt.
Nach der Vorstellung der allgemeinen Relativitätstheorie ist also die Gravitation keine richtige Kraft. Durch richtige Kräfte wie etwa die elektromagnetische Kraft würden die Steine von den Geodäten (Geraden) weggezogen.
5. Newtons Gravitationsgesetz als erste Näherung
Die Schwierigkeit ist offensichtlich, die gekrümmte Geometrie zu zeichnen und sich die Bewegungen darin vorzustellen. Ich möchte hier eine alternative Darstellung zeigen, in der die Koordinatensysteme nicht gekrümmt gezeichnet werden. Wieder nehmen wir an, dass sich alle Teilchen mit Lichtgeschwindigkeit durch die Raumzeit bewegen. Teilchen, die im dreidimensionalen Raum ruhen, bewegen sich mit Lichtgeschwindigkeit durch die Zeit.
Den Aufenthaltsort eines Teilchens können wir in ein Koordinatensystem einzeichnen (ich beschränke mich hier auf zwei Raumdimension). Den Ablauf der Zeit kann ich dann so darstellen, dass ich verschiedene Koordinatensysteme schichtenweise übereinander lege. Wie in einem Film laufen die einzelnen Bilder hintereinander ab (Abbildung 5).
Abbildung 5 Eine Kugel ruht im Raum (nur zwei Dimensionen sind gezeichnet). Der Ablauf der Zeit kann als Bewegung durch eine andere Dimension angesehen werden. Wir können die Zeit sogar statt in Sekunden in Metern angeben, indem wir einfach alle Zeitangaben mit c multiplizieren. Die Kugel fliegt dann sozusagen mit Lichtgeschwindigkeit durch die Zeit, während sie im Raum ruht.
Statt nun das Koordinatensystem gekrümmt zu zeichnen, können wir uns auch vorstellen, die Bewegung durch dieses Koordinatensystem sei nicht überall gleich gut möglich. Gravitationsfelder sind wie ein Sumpf, in dem nur eine langsame Bewegung möglich ist. Das Teilchen, das sich durch die Zeit bewegt, wird deshalb auf der unteren Seite stärker gebremst als auf der oberen. Dabei geschieht das gleiche, wie bei einem Wagen, der auf einer Seite in den Randstein fährt: Der Wagen wird auf dieser Seite gebremst und dreht erst recht in Richtung Randstein. Genau so wird das Teilchen nach unten abgelenkt, wenn es unten gebremst wird. (Abbildung 6).
Abbildung 6 Statt sich die Raumzeit gekrümmt vorzustellen, können wir uns auch annehmen, die Bewegung durch die Zeit sei für Teilchen oben schneller als für Teilchen unten. Die Teilchen werden dann unten abgebremst und nach unten abgelenkt.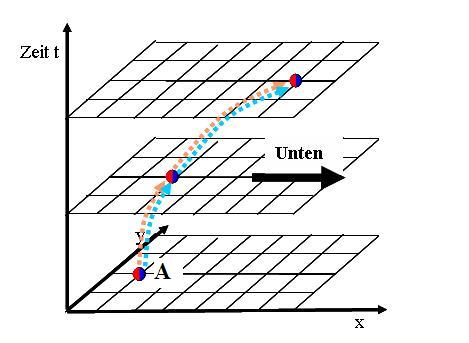
In Abbildung 6 scheint es, dass das Teilchen sehr bald nicht mehr in t Richtung fliegt, sondern nur noch durch den Raum. Wenn dies geschehen würde, würde das Argument mit der Abbremsung nicht mehr funktionieren oder zumindest zahlenmässig anders aussehen. In der Praxis ist dies aber nie ein Problem. Pro Sekunde fliegt das Teilchen 300´000 km durch die Zeit. Bei den üblichen Gravitationsbeschleunigungen wird es aber höchstens einige Meter nach unten abgelenkt. In Abbildung 6 ist also ein viel zu grosser Bogen gezeichnet. In der Praxis können wir sagen:
“Das Teilchen fliegt praktisch nur durch die Zeit, denn die Geschwindigkeit durch den Raum ist weit von der Lichtgeschwindigkeit entfernt. Die Abbremsung auf der blauen Bahn gegenüber der roten Bahn ist deshalb praktisch konstant. Das heisst, das Teilchen bewegt sich zum Zeitpunkt A praktisch auf einer Kreisbahn durch die Raumzeit.”
Nach dem obigen Modell fliegt das Teilchen also mit der Lichtgeschwindigkeit c durch die Raumzeit und erfährt durch die Abbremsung eine Kreisbeschleunigung aKreis für die gilt:
aKreis = c2/R (1)
R ist der sehr grosse Radius dieses Kreises in der Raumzeit. Im Punkt A zeigt die Kreisbeschleunigung in x-Richtung. Ich will nun zeigen, dass aKreis gerade die bekannte Gravitationsbeschleunigung g ist. Im Artikel Effekte der allgemeinen Relativitätstheorie leite ich die Formel für Zeitdilatation aus der Gravitationsbeschleunigung her:
Toben = (1+gΔx/c2)Tunten (2)
Dabei ist g die Gravitationsbeschleunigung und Dx ein kleiner, senkrechter Abstand in einem Gravitationsfeld, z. B. die Höhe einen Turmes. Man könnte sich z. B. vorstellen, dass auf einem Turm der Höhe Dx eine Uhr positioniert ist und auf der Erde unten liegt eine andere Uhr. Bei der Herleitung der Formel (1) habe ich angenommen, dass Licht wie Teilchen im Gravitationsfeld hinunterfällt und dabei Energie gewinnt. Daraus ergibt sich die Zeitverlamsamung.
Hier gehe ich umgekehrt vor: Ich nehme an, der elementare Effekt ist die Verlangsamung der Zeit nach der Formel (2), wobei g nur irgend eine Konstante ist. Ich zeige, dass g gerade die Kreisbeschleunigung aKreis ist, dass also das Teilchen durch die Zeitdilatation genau mit g nach unten beschleunigt wird.
Abbildung 7 Ein Teilchen mit Durchmesser Δx bewegt sich mit Lichtgeschwindigkeit durch die Zeit. Dabei wird es unten abgebremst. Wenn sich der obere Teil des Teilchens (pink) um cToben durch die Zeit bewegt, kommt der untere Teil (blau) nur cTunten. Dadurch wird das Teilchen auf einen Kreis mit dem Radius R gelenkt, wobei die Kreisbeschleunigung aKreis=c2/R ist.
Mit (2) und dem Strahlensatz erhalten wir:
Tunten / R = Tunten (1+gΔx/c2) / (R + Δx) (3)
Und nach g aufgelöst:
g = c2 / R = aKreis (4)
Die Gravitationsbeschleunigung wird also durch die Zeitverlangsamung vollständig erklärt. Wir brauchen keine zusätzliche Ursache der Gravitationskraft zu suchen. Eine genaue Analyse ergibt zwar eine kleine Korrektur: Damit die Lichtgeschwindigkeit auch bei Zeitverlangsamung vom Beobachter unabhängig ist, muss auch der Raum gekrümmt sein (Eps 1), (Olo 1). Für alle Bewegungen aus unserem Alltag hat diese Korrektur aber keine Bedeutung. Denn die Bewegungen aus unserem Alltag sind ja alle langsam sind im Vergleich zur Lichtgeschwindigkeit, das heisst, sie bewegen sich fast ausschliesslich durch die Zeit und kaum durch den Raum.
Für Fachleute muss ich noch erwähnen, dass Physiker normalerweise mit einer anderen Metrik rechnen, nämlich mit der Minkowski-Metrik. Die obige Darstellung kann man aber problemlos in die Minkowski-Metrik umrechnen (Eps 1).
6. Die allgemeine Relativitätstheorie aus Sicht des Poeten
Bernhard Shaw fasste den Unterschied zwischen Newtons und Einsteins Ideen sehr schön zusammen: „Als Engländer postulierte Newton ein geradliniges Universum. Denn die Engländer benützen stets das Wort ‘square’ (senkrecht) für Ehrlichkeit, Wahrhaftigkeit, kurz: Gradlinigkeit. Newton wusste, dass das Universum bewegte Körper enthielt und dass keiner von diesen sich auf einer geraden Linie bewegte und dies auch nicht konnte. Aber als Engländer liess er sich von diesen Fakten nicht beeindrucken. Zur Erklärung, weshalb alle Linien in seinem gradlinigen Universum gebogen waren, führte er eine Kraft namens Gravitation ein, errichtete auf dieser Idee ein kompliziertes britisches Universum und erhob dieses zur Religion, der während 300 Jahren gehuldigt wurde.
… 300 Jahre später taucht ein junger Professor in Mitteleuropa auf und sagt, die Gravitationskraft sei eine sehr nützliche Hypothese und ihre Resultate kämen der Wahrheit in den meisten Fällen ziemlich nahe. Aber er persönlich komme auch ohne sie aus. Man forderte von ihm eine Erklärung, weshalb denn, wenn es keine Gravitationskraft gebe, die himmlischen Körper nicht geradeaus fliegen. Denn dies widerspreche doch klar der Natur des Universums. Er antwortete, dazu bedürfe es keiner Erklärung, weil das Universum nicht gradlinig und exklusiv britisch sei: Es ist gekrümmt…“
7. Weitere Artikel zu ähnlichen Themen:
Mehr zum Thema Krümmung der Raumzeit und wie die Gravitation im Universum als Ganzes aussieht unter:
Urknall
Effekte der allgemeinen Relativitätstheorie
Wie kann der Raum gekrümmt sein?
8. Weiterführende Bücher:
Philip Wehrli, ‘Das Universum, das Ich und der liebe Gott’, (2017), Nibe Verlag,

In diesem Buch präsentiere ich einen Gesamtüberblick über mein Weltbild: Wie ist das Universum entstanden? Wie ist das Leben auf der Erde entstanden? Was ist Bewusstsein und woher kommt es? Braucht es dazu einen Gott?
Viele Artikel dieses Blogs werden in diesem Buch in einen einheitlichen Rahmen gebracht, so dass sich ein (ziemlich) vollständiges Weltbild ergibt.
Leserunde bei Lovelybooks zum Buch ‘Das Universum, das Ich und der liebe Gott’, von Philipp Wehrli (abgeschlossen)
Rezensionen bei Lovelybooks
Rezensionen bei Amazon
Film-Präsentation zum Buch
Nibe Verlag
Einstein Albert, ‘Über die spezielle und die allgemeine Relativitätstheorie, gemeinverständlich’, Springer, (1916)
Nach wie vor eine der besten Einführungen in die Relativitätstheorie, das Werk von ihrem Schöpfer selbst.
Sexl Roman u. Hannelore, ‘Weisse Zwerge – Schwarze Löcher’, (1979), Vieweg Studium, Braunschweig
Wie alle Bücher von Sexl didaktisch hervorragend und sehr sorgfältig geschrieben. Ideal als erster Kontakt mit der allgemeinen Relativitätstheorie. Verwendet einige einfache mathematische Formeln.
Epstein Lewis C., ‘Relativitätstheorie anschaulich dargestellt’, Birkhäuser, (1983), Basel
Von diesem Buch bin ich begeistert! Ohne Mathematik zeigt Epstein, wie die Krümmung der Raumzeit zur Gravitationskraft führt, wie die Lichtablenkung an grossen Massen zustande kommt und wie schwarze Löcher funktionieren.
Oloff Rainer, ‘Geometrie der Raumzeit – Eine mathematische Einführung in die Relativitätstheorie’, (1999), Vieweg, Braunschweig
Das Buch ist geschrieben für Studenten der Mathematik oder Physik, die in einem einsemestrigen Kurs von zwei Doppelstunden plus Übungen die allgemeine Relativitätstheorie wirklich verstehen wollen. Oloff erklärt bei jeder Definition und jedem Satz, wozu er sie braucht. Die Erklärungen sind anwendungsorientiert und verständlich. Ein ausgezeichnetes Buch für Physikstudenten!
9. Externer Link
Animation zur Erklärung der Gravitation nach der Idee von Lewis C. Epstein.