Visits: 1977
Philipp Wehrli, 2. Januar 2002
Die Polarisation von Licht ist ein Wellenphänomen, das wie viele Welleneffekte unserer Intuition widerspricht. Wer die Wellen der Quantentheorie verstehen will, muss auch das Verhalten der klassischen Wellen verstehen. Die quantitative Beschreibung der Polarisation, die hier eingeführt wird, ist für das Verständnis des Einstein-Podolsky-Rosen Experimentes Voraussetzung, das wohl den Höhepunkt der Quantenphilosophie darstellt.
1. Lineare Polarisation
Anders als Schallwellen, die nur vorwärts und rückwärts schwingen, schwingen elektromagnetischen Wellen, also Photonen, senkrecht zur Ausbreitungsrichtung. Weitere elektromagnetische Wellen sind zum Beispiel Radiowellen, Mikrowellen, UV-Strahlung und Infrarot. Alle diese Wellen sind zusammengesetzt aus einer elektrischen und einer magnetischen Komponente und das elektrische Feld schwingt immer senkrecht zum magnetischen. Wie genau das elektrische und das magnetische Feld zusammenhängen, beschreiben die Maxwell-Gleichungen.
Abbildung 1 Licht ist (klassisch betrachtet) eine elektromagnetische Welle. Das elektrische Feld steht senkrecht zu einem magnetischen Feld und beide stehen senkrecht zur Ausbreitungsrichtung.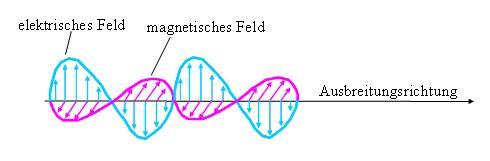
Wer funkt oder schon mal eine Radioantenne eingestellt hat, kennt das Phänomen der Polarisation. Radiowellen können von der Antenne nur dann absorbiert werden, wenn ihr elektrisches Feld in der Richtung der Antenne schwingt. Genau dasselbe gilt auch für Licht. Wenn man in einem Glas gewisse fadenförmige Moleküle in einer bestimmten Richtung ausrichtet, wirken diese wie Antennen auf die Lichtwellen. Alles Licht, dessen elektrische Komponente in der Richtung der Moleküle schwingt, wird absorbiert. Schwingt aber die magnetische Komponente in die Richtung der Fadenmoleküle, so kann das Licht durch das Glas hindurch. Solche Gläser nennt man Polarisationsfilter oder Polarisatoren. Ich verwende in diesem und im nächsten Kapitel die Wörter ‘Polarisationsfilter’, ‘Polarisator’ und ‘Filter’ synonym und meine damit immer solche Gläser mit Fadenmolekülen drin.
Die folgenden Experimente kann man sehr leicht selber durchführen. Gebrauchte Polarisationsfilter kann man in vielen Fotoshops recht günstig kaufen.
Zunächst richten wir zwei Polarisationsfilter hintereinander gleich aus. Wir stellen fest, dass so alles Licht, das durch den ersten Filter gelangt, auch durch den zweiten geht.
Abbildung 2 Werden zwei gleichgerichtete Polarisationsfilter hintereinandergestellt, so geht alles Licht, das durch den ersten Filter gelangt, auch durch den zweiten. In den Bildern ist nur die magnetische Komponente des Lichtes gezeichnet. (Normalerweise zeichnet man die elektrische Komponente. Aber diese wird genau dann am Gitter absorbiert, wenn sie parallel zu ihm schwingt. Weil dies seltsam aussehen würde, zeichne ich die magnetische Komponente.)
Wenn wir jetzt aber den zweiten Filter um 90° drehen, kann das Licht plötzlich nicht mehr hindurch. Alles, was nicht vom ersten Filter absorbiert wird, bleibt am zweiten hängen.
Abbildung 3 Werden zwei senkrecht zueinander polarisierte Filter hintereinander gestellt, so kommt kein Licht durch.
Durch die obigen zwei Filter zusammen kann also kein Licht hindurch. Das erstaunt vielleicht nicht speziell. Das entspricht unserer Alltagserfahrung: Je mehr Hindernisse man in den Weg stellt, desto weniger kommt durch. Nun stellen wir aber noch einen zusätzlichen Filter dazwischen, also noch ein Hindernis mehr. Und plötzlich kommt das Licht wieder durch!
Abbildung 4 Stellen wir zwischen die zwei senkrecht zueinander gerichteten Polarisatoren einen dritten, der zu beiden anderen um 45° gedreht ist, so kommt wieder Licht hindurch. Die grauen Pfeile zeigen die Amplitude des Magnetfeldes, das beim Filter ankommt. Die schwarzen Pfeile zeigen die Amplitude des Magnetfeldes, das durch den Filter hindurchgeht.
Man könnte sagen, die Lichtwelle werde durch den mittleren Polarisator leicht gedreht, so dass plötzlich ein Teil davon doch durch den hinteren Filter hindurch kann. Der Versuch funktioniert mit einer gewöhnlichen Lampe, er funktioniert aber auch mit einzelnen Photonen.
Um das Einstein-Podolsky-Rosen Experiment (EPR) zu verstehen, müssen wir diesen Effekt an Polarisatoren auch quantitativ verstehen. Wieder schicken wir Photonen hintereinander durch zwei Polarisatoren. Welcher Anteil der Photonen, die durch den ersten Polarisator gehen, geht auch durch den zweiten Polarisator, der um den Winkel gegen den ersten gedreht ist?
Nach dem ersten Filter hat die Lichtwelle eine bestimmte Höhe, die sogenannte Amplitude A0. Man kann sich A0 als Pfeil vorstellen. Bei gewöhnlichen Wellen ist |A0|2 proportional zur Intensität, bzw. zur Energie der Welle. Bei Lichtwellen ist |A0|2 proportional zur Anzahl der Photonen in der Welle. Wenn nur ein Photon losgeschickt wird, ist |A0|2proportional zur Wahrscheinlichkeit, dass das Teilchen in diesem Teil der Welle ist. Weil A0 die Amplitude unseres Anfangsstrahles ist, setzen wir |A0|2=100%. Das soll sagen: 100% der Photonen, die wir betrachten, befinden sich im Anfangsstrahl, d.h. nach dem ersten Filter.
Trifft die Welle auf einen zweiten Polarisationsfilter, so wird die Amplitude auf die Richtung des Polarisationsfilters projiziert. (vgl. Abbildung 5). Diese Projektion ergibt gerade die Amplitude der neuen Welle.
Abbildung 5 Eine senkrecht schwingende Lichtwelle mit der Amplitude A0 wird auf einen Polarisator geschickt, der um den Winkel α gegen die Senkrechte gedreht ist. Die Welle wird in zwei Teilwellen zerlegt. Nämlich erstens in eine Teilwelle, die parallel zu den Fadenmolekülen im Polarisator schwingt: Diese Welle hat die Amplitude A·cos a und kommt durch den Filter hindurch. Zweitens eine Teilwelle, die gerade senkrecht zu den Fadenmolekülen schwingt: Diese Welle hat die Amplitude A·sin a und wird absorbiert. Wie oben ist hier die Amplitude des magnetischen Feldes der Welle gezeichnet.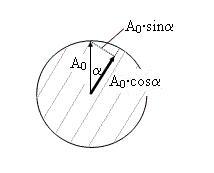
Ist die obige Interpretation von |A0|2 als Intensität haltbar? Wenn die Anfangswelle mit der Amplitude A0 in zwei Teilwellen aufgespalten wird, so müssen alle Photonen aus der Anfangswelle in einer der beiden Teilwellen sein. Tatsächlich ist dies erfüllt. Denn nach dem Satz von Pythagoras gilt:
|A0|2 = |A0·cos α|2 + |A0·sin α|2
Diese Gleichung sagt: Die Intensität des Anfansstrahls ist gleich der Summe der Intensitäten seiner Teilwellen.
Wie viel Licht kommt nun durch zwei Polarisationsfilter, die in einem Winkel α gegeneinander gedreht sind? -Ein Photon, das durch den ersten Filter gelangte, kommt mit einer Wahrscheinlichtkeit
P = |A0·cos α|2
auch durch den zweiten Filter. In der folgenden Tabelle sind die Wahrscheinlichkeiten für einige spezielle Winkel berechnet. Wieder ist P, die Wahrscheinlichkeit, dass ein Photon aus dem Anfangsstrahl durch den zweiten Filter hindurchgeht. Weil wir A0=100%=1 gesetzt haben, ist
P=|cos α|2.
| Winkel α | P = |cos α|2 | Winkel α | P = |cos α|2 | |
| 0° | 100 % | 180° | 100 % | |
| ±30° | 75 % | ±210° | 75 % | |
| ±60° | 25 % | ±240° | 25 % | |
| ±90° | 0 % | ±270° | 0 % |
2. Zirkulare Polarisation
Im obigen Beispiel habe ich elektromagnetische Wellen betrachtet, bei denen der elektrische Anteil immer in die gleiche Richtung schwingt. Solche Wellen nennt man linear polarisiert. Eine andere Art von Polarisation ist die links- und die rechtszirkulare Polarisation, bei der das elektrische Feld nicht immer in der gleichen Richtung schwingt. Vielmehr dreht sich die Schwingungsachse langsam. Das elektrische Feld wird dabei nie mehr ganz null, sondern es bleibt vom Betrag her gleich und ändert nur die Richtung.
Zirkulare Polarisation erreicht man, indem man eine linear polarisierte Lichtwelle durch einen Kristall schickt, in dem die Fortpflanzungsgeschwindigkeit von der Schwingungsachse des elektrischen Feldes abhängt. In Abbildung 6 ist (anders als in Abbildung 1!) nur das elektrische Feld eingezeichnet! Allerdings wurde dieses in zwei Komponenten zerlegt. Eigentlich würde es schräg schwingen im Winkel j zur optischen Achse. Ein elektrisches Feld kann man aber wie einen Vektor in Komponenten zerlegen und genau dies wurde in Abbildung 6 getan. Man könnte auch sagen: Die Welle in Abbildung 6 ist eine Überlagerung zweier senkrecht aufeinander stehender linear polarisierter Wellen.
Das Spezielle ist nun, dass die waagrechte Komponente sich im l/4 Plättchen langsamer fortpflanzt als die senkrechte.
Abbildung 6 (Von Wikipedia zur freien Verfügung gestellt, besten Dank!)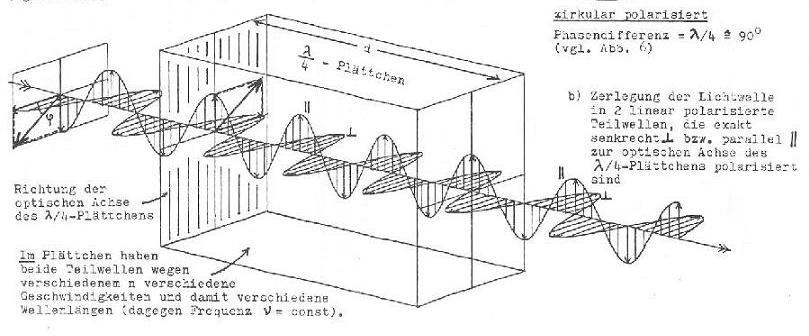
Das l/4-Plättchen bremst die waagrechte Komponente um 1/4 der Wellenlänge. Die Abbildung 7 zeigt die Wirkung dieser Abbremsung. Hier sind die zwei Komponenten des E-Feldes wieder zusammengezählt, und wir sehen, dass aus dem linear polarisierten Licht, rechtszirkulares Licht entsteht (Abbildung 7). Ein weiteres, gleich gerichtetes l/4-Plättchen hätte wieder linear polarisiertes Licht zur Folge, diesmal aber orthogonal zum ursprünglichen. Drei solche Plättchen würden zu linkszirkularem Licht führen.
Abbildung 7 (Von Wikipedia zur freien Verfügung gestellt, besten Dank!)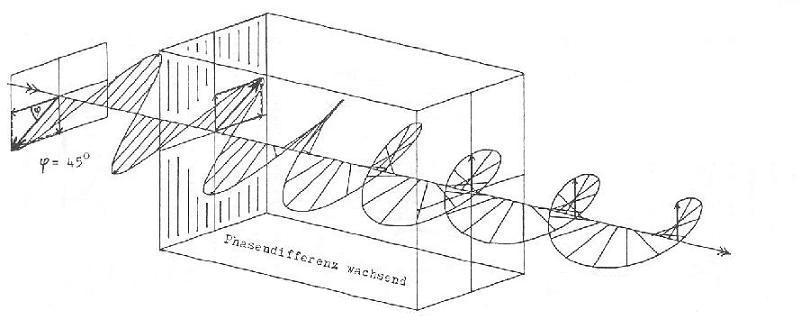
Achtung: Die Wirkung eines l/4-Plättchens hängt von der ursprünglichen Polarisation des Lichtes ab. Ist das Licht vor dem Plättchen parallel oder waagrecht zur optischen Achse polarisiert, so geschieht entweder gar nichts oder es wird die gesamte Welle etwas gebremst, was auch nicht sichtbar ist. Schwingt das Licht im 45°-Winkel zur optischen Achse, so ergibt sich rechtszirkulares Licht. Beim Winkel von -45° dreht sich das Licht genau in die andere Richtung, es wird also linkszirkular.
3. Vergleich zwischen linearer und zirkularer Polarisation
Wellenplatten führen im Gegensatz zu den oben geschilderten linearen Polarisationsfiltern nicht zu einem Verlust an Licht, abgesehen von der Reflexion, die es auch bei einer Linse gibt. Während bei den oben geschilderten linearen Filtern nur die Hälfte der Photonen hindurch geht, sind die Wellenplatten im Idealfall verlustfrei.
Wie in Abbildung 6 ersichtlich, kann eine zirkular polarisierte Welle als Überlagerung zweier linear polarisierter Wellen gesehen werden.
Ebenso kann man durch geeignete Überlagerung einer rechts- und einer linkszirkularen Welle nach Wahl eine senkrecht oder eine waagrecht polarisierte Welle erhalten.
So wie zwei senkrecht polarisierte Lichtwellen bei der Überlagerung keine Interferenzmuster zeigen, können auch eine rechts- und eine linkszirkular polarisierte Welle nicht interferieren, denn auch sie stehen orthogonal zueinander.
Weiterführende Artikel
Maxwell-Gleichungen – Das Licht als elektromagnetische Welle
Das Doppelspaltexperiment (Licht kann nicht rein klassisch verstanden werden)
Weiterführende Bücher:
Philip Wehrli, ‘Das Universum, das Ich und der liebe Gott’, (2017), Nibe Verlag,

In diesem Buch präsentiere ich einen Gesamtüberblick über mein Weltbild: Wie ist das Universum entstanden? Wie ist das Leben auf der Erde entstanden? Was ist Bewusstsein und woher kommt es? Braucht es dazu einen Gott?
Viele Artikel dieses Blogs werden in diesem Buch in einen einheitlichen Rahmen gebracht, so dass sich ein (ziemlich) vollständiges Weltbild ergibt.
Leserunde bei Lovelybooks zum Buch ‘Das Universum, das Ich und der liebe Gott’, von Philipp Wehrli (abgeschlossen)
Rezensionen bei Lovelybooks
Rezensionen bei Amazon
Film-Präsentation zum Buch
Nibe Verlag
