Diracs grosse Zahlen

Visits: 2036

Philipp Wehrli, 13. Oktober 2006

Paul Dirac

Paul Dirac und Arthur Eddington entdeckten, dass die Zahl 10⁴⁰ in der Natur bemerkenswert oft und in völlig verschiedenen Zusammenhängen vorkommt. Ich zeige in diesem Text, wie Grössen aus völlig verschiedenen Gebieten wie der Nukleonenradius oder die elektrische Ladung mit der Grösse unseres Universums oder der Anzahl Teilchen in unserem Universum zusammenhängen.

1. Diracs grosse Zahlen

1.1. Längen

Aus der Elektronenladung, der Elektronenmasse und der Lichtgeschwindigkeit können wir in natürlicher Weise eine Längeneinheit konstruieren:
r₀ = e² / (4πε₀m_e c²) = 2,8178 · 10^-15 m
Diese Länge entspricht dem klassischen Elektronenradius. Wir erhalten diesen Radius, indem wir annehmen, dass die gesamte Masse, also die Energie des Elektrons vom elektrischen Feld stammt. Wenn die elektrische Ladung des Elektrons gleichmässig in einer Kugel mit Radius r₀ versammelt ist, so hat diese Kugel gerade die Ruheenergie, also die Ruhemasse des Elektrons.

Diese Zahl sagt nichts über die Natur aus, denn sie hängt offensichtlich von unseren Einheiten ab. Hätte ich z. B. die Lichtgeschwindigkeit in km/s statt in m/s angegeben, so wäre das Resultat anders geworden. Wir können aber r₀ als natürlichen Massstab benützen und mit diesem Massstab das Universum ausmessen.

(1)       R_Universum / r₀ = 10²⁶ m / r₀ = 3,5 · 10⁴⁰

Es haben also etwa 10⁴⁰ Elektronen nebeneinander im Universum Platz. Diese Zahl ist unabhängig von unseren Einheiten: Auch ein ausserirdischer Physiker würde genau auf diese Zahl kommen.

1.2. Zeiten

Licht benötigt
t₀ = r₀ / c = e² / (4πε₀m_e c³) = 9,399 · 10^-24 s,
um die Elementarlänge r₀ zu durchqueren. t₀ kann als elementare Zeiteinheit angesehen werden. Das Alter unseres Universums ist etwa:
T_Universum = 13,5 Mrd. Jahre = 4,257 · 10¹⁷ s
Wenn wir das Alter des Universums in der obigen elementaren Zeiteinheit messen, ergibt sich:
(2)       T_Universum/ t₀ = 4,257 · 10¹⁷ s / 9,399 · 10^-24 s = 4,5 · 10⁴⁰

1.3. Kräfte

Die elektrische Kraft zwischen einem Proton und einem Elektron ist F_e=e²/4pe₀r²; die Gravitationskraft ist F_G=Gm_nm_e/r². Das Verhältnis dieser beiden Kräfte ist unabhängig vom Abstand der Teilchen.

(3)       F_e / F_G = e² / 4πε₀Gm_nm_e = 2,27 · 10³⁹

1.4. Teilchenzahl

Die Gravitationskraft in unserem Universum stammt im Wesentlichen von den Nukleonen, also von Protonen und Neutronen, die beide praktisch die gleiche Masse haben. Die Masse des Universums geteilt durch die Masse eines Protons ergibt also ziemlich genau die Anzahl der Nukleonen. Die Masse des Universums beträgt etwa 10⁵² kg wir erhalten also

(4a)     M_Universum / m_n = 6 ·10⁷⁸
also etwa 10⁴⁰· 10⁴⁰.

Da die Masse des Universums zum grossen Teil von den Nukleonen stammt, ist die Anzahl Nukleonen ziemlich genau

(4b)     10⁸⁰.

1.5. Beziehung zwischen Nukleonen und den Planckschen Einheiten

Von Amateuren hört man oft die Vermutung, Elementarteilchen seien schwarze Löcher. Tatsächlich ist aber z. B. das Proton viel zu gross, um ein schwarzes Loch zu sein. Damit ein Proton zu einem schwarzen Loch kollabieren würde, müsste sein Radius
r_G = 2Gm_n/c² = 2,484 · 10^-54 m
sein. Tatsächlich ist er von derselben Grössenordnung wie r₀, also

(5)       r₀/r_G = 1,13 · 10³⁹

Bemerkenswerterweise liegt der Radius des kleinsten möglichen schwarzen Lochs, die sogenannte Planck-Länge ziemlich genau zwischen diesen zwei Massen. Es gilt:

(6)       l_Pl / r_G = 1,61624 · 10^-35 m / 2,484 · 10^-54 m = 6.507 · 10¹⁸

(7)       r₀/l_Pl = 2,8178 · 10^-15 m / 1,61624 · 10^-35 m = 4.554 · 10²⁰

Was bemerkenswert ist, da 10²⁰ die Wurzel von 10⁴⁰ ist. Umgekehrt ist die Plancksche Masse um fast 10²⁰-mal grösser als die Masse des Protons.

(8)       m_Pl /m_n = 2,17645 · 10^-8 kg / 1,6726 · 10^-27 kg = 1,3 · 10¹⁹

Das ist richtig: Die Masse des schwarzen Lochs wäre grösser, aber die Ausdehnung wäre kleiner als beim Proton.

2. Zufall oder nicht?

Als ich noch als Schüler zum ersten Mal von Diracs grossen Zahlen las, dachte ich: „Das ist doch einfach Zufall! Die Zahlen stimmen ja nicht einmal besonders gut überein.“ Diracs grosse Zahlen lassen sich aber nicht so ohne weiteres als Zufall abtun, wie Harrison an einer schönen Übungsaufgabe zeigt (Har 1). In meinen Worten:

Angenommen, eine Zahl N₁ ist 10⁴⁰. Von einer anderen Zahl N₂ wissen wir, dass sie jeden Wert von 1 bis 10¹⁰⁰ annehmen kann. Wie gross ist die Wahrscheinlichkeit, dass N₂ innerhalb eines Faktors 100 gleich N₁ ist?

N₂ müsste also zwischen 10³⁸ und 10⁴² liegen, damit die Bedingung erfüllt ist. Es gibt 10⁴²-10³⁸=0.9999 · 10⁴², also praktisch 10⁴² Zahlen, die dies leisten. Ich unterteile also den erlaubten Bereich von 1 bis 10¹⁰⁰ in Abschnitte von 10⁴² Zahlen und sehe, dass es fast 10⁵⁸ solche Abschnitte gibt. In jedem dieser Abschnitte könnte meine Zahl N² mit der gleichen Wahrscheinlichkeit zu liegen kommen. Die Wahrscheinlichkeit für ein Zusammentreffen ist also 1/10⁵⁸, also praktisch 0. Es kann nicht sein, dass zwei so grosse Zahlen so nah beieinander liegen. Selbst wenn die Zahlen nicht genau gleich sind, selbst wenn sie sich um Faktor 100 unterscheiden, muss es einen Grund geben, weshalb sie von der Grössenordnung her gleich sind.

Dass Harrison hier einen Überlegungsfehler machte, merkte ich erst, als mich im dsp Physikforum jemand darauf aufmerksam machte. Harrison nahm nämlich an, die Zahlen seien gleichverteilt. Sie könnten aber auch logarithmisch verteilt sein. Es könnte z. B. zu jeder Zehnerpotenz eine bedeutende Zahl geben. Dann wäre das obige Zusammentreffen durchaus durch Zufall zu erklären. Wenn ich dies früher gemerkt hätte, hätte ich mich wohl kaum mit diesen Zahlen befasst und ich hätte den folgenden Zusammenhang nicht gefunden. Mir scheint aber, die Zahlen lassen sich überhaupt ohne Zufall erklären.

Weiter scheint seltsam, dass scheinbar willkürlich irgendwelche Grössen miteinander verglichen werden, die offensichtlich keinen Bezug zueinander haben. Mal wird der Radius des Elektrons genommen, mal die Masse des Protons. Weshalb nicht umgekehrt? Wir kennen heute sehr viele Teilchen. Weshalb wurde nicht der Radius von irgendeinem anderen Teilchen als Massstab gewählt? Mit all den Teilchen wird man ja wohl irgendwelche Zahlen finden, die zusammen passen.

Menschen haben ein ausgesprochenes Geschick, solche zufälligen Übereinstimmungen zu finden und sich darüber zu wundern. Gero von Randow zeigt in seinem hübschen Büchlein ‚mein paranormales Fahrrad’, wie man solche Übereinstimmungen bei jedem beliebigen Gegenstand finden kann, wenn nur genügend Zahlen im Spiel sind (Ran 2).

Bei näherer Betrachtung ist aber die Wahl nicht willkürlich. Die Masse der Nukleonen macht den Hauptteil der Masse des Universums aus. In kosmologischen Modellen hängt die Materiedichte im Universum eng mit der Expansion des Universums zusammen. Es ist also nicht völlig überraschend, dass ein Zusammenhang zwischen der Grösse des Universums und der Masse der wichtigsten Teilchen besteht. Weshalb aber soll ich die Grösse des Universums in Elektronen- und nicht in Nukleonenradien messen?

Bemerkenswerterweise ist der klassische Elektronenradius von der gleichen Grössenordnung wie der Durchmesser der Nukleonen. Manche Autoren vergleichen deshalb nicht den Elektronenradius, sondern die Compton-Wellenlänge des Nukleons mit dem Radius des sichtbaren Universums und erhalten dabei die gleiche Übereinstimmung (wie gesagt, auf einen Faktor 10 kommt es bei so grossen Zahlen überhaupt nicht an, solche kleinen Fehler kann man später wohl immer noch korrigieren).

3. Erklärungsversuch

Von den obigen Gleichungen lassen sich einige sehr leicht auf andere zurückführen. Für den Laien klingt es dann beeindruckend, wie viele Dinge da so präzise miteinander zusammen hängen. In Wirklichkeit habe ich vieles mehrmals in verschiedenen Ausdrücken gesagt. Das Rätsel wird wesentlich übersichtlicher, wenn ich den Wald von Gleichungen ein wenig durchforste.

Zunächst aber möchte ich noch eine andere Frage lösen. Ich habe erwähnt, dass der klassische Elektronenradius fast gleich der Compton-Wellenlänge des Protons ist. Tatsächlich lassen sich die meisten von Diracs grossen Zahlen auf diese Tatsache zurückführen. Diese Übereinstimmung ist also ein zentraler Punkt. Kann sie weiter begründet werden?

3.1. Übereinstimmung zwischen den ‚Grössen’ von Elektronen und Protonen

Der Begriff ‚Grösse’ steht in Anführungszeichen, weil es verschiedene Möglichkeiten gibt, die Grösse von Elementarteilchen zu definieren. In gewissem Sinne sind Elektronen punktförmig. Dennoch können wir dem Elektron einen Radius zuordnen, der charakteristisch ist. Dazu nehmen wir naiv an, die gesamte elektrische Ladung des Elektrons sei in eine Kugel mit dem Radius r_e gepackt. Die Energie des elektrischen Feldes setzen wir dann gleich der Ruheenergie des Elektrons:
m_ec² = 1/4πε₀ · e²/r_e

Daraus ergibt sich für den Radius:
r_e = e²/4πε₀m_ec² = 2,8178 · 10^-15 m

Die Compton-Wellenlänge des Nukleons misst:
λ_n = h/m_nc = 1.321 · 10^-15 m

Überall, wo ich oben den Elektronenradius eingesetzt habe, hätte ich also auch λ_n einsetzen können und umgekehrt. Manche der grossen Zahlen sehen dadurch nicht ganz so willkürlich aus. Aber das Rätsel hat sich nur verlagert: Woher kommt die Übereinstimmung zwischen den ‚Radien’ von Elektron und Proton?

Verschiedene Physiker begründen dieses Zusammentreffen –meiner Ansicht nach überzeugend- mit dem anthropischen Prinzip. Es wären durchaus Welten denkbar, in denen die wichtigsten Elementarteilchen völlig unterschiedliche Grössen hätten. In solchen Welten könnten sich aber keine Moleküle und damit auch kein Leben bilden. Es ist deshalb nicht überraschend, dass wir eine Welt beobachten, in der die Teilchen so schön aufeinander abgestimmt sind.

Man mag durchaus leise Zweifel haben, ob Elektronen und Protonen tatsächlich im obigen Sinne gleich gross sein müssen, um dem anthropischen Prinzip zu genügen. Sicher ist es aber weniger erstaunlich, dass die zwei wichtigsten Elementarteilchen auf Faktor 100 genau gleich gross sind, als dass zwei Zahlen der Grösse 10⁴⁰, die zudem aus völlig verschiedenen Gebieten der Physik stammen, gleich gross sind.

3.2. Kräfte und Plancksche Einheiten

Ich setze also die Gleichheit von r_e und λ_n voraus. Ausserdem definiere ich:

E₁ := elektrische Kraft / Gravitationskraft = ca. 10⁴⁰

Mit dieser Definition gilt offensichtlich Satz (3). Mit dieser Definition und der obigen Annahme beweise ich nun nacheinander die Sätze (8), (7), (5) und (6). Es wird sich herausstellen, dass die Sätze (7) und (5) um einen Faktor zwei daneben liegen. Weil die Zahl E₁ so gross ist, ist dies immer noch eine ausserordentliche Übereinstimmung und im Rahmen des Erlaubten. Tatsächlich sind die gemessenen Zahlen bei (7) und (5) eher zu klein, wie dies in den folgenden Beweisen zu erwarten ist.

Beweis von Satz (8):

r_e = e²/4πε₀m_ec² = h/m_nc = λ_n              || · c²/Gm_n

e² / 4πε₀Gm_nm_e = hc/Gm_n²

F_e / F_G = m_Pl²/m_n²                  || ( )^1/2

m_Pl/m_n = E₁^1/2 = ca. 10²⁰

Beweis von Satz (7):

Nach (8) gilt:
m_Pl²/m_n² = E₁

Einsetzen (h ist die Plancksche Konstante h/2π):
E₁ = m_Pl²/m_n² = hc/Gm_n² = 4 · Gh/c³ · c⁴/4G²m_n²

E₁ = 4 · l_pl² : r_g²                      || ( )^1/2

E₁^1/2 = 2 · l_Pl / r_G

Wie oben erklärt, macht der Faktor 2 bei so grossen Zahlen keinen Unterschied. Satz (7) ist somit bewiesen.

Beweis von Satz (5):

Nach Definition gilt:
E₁ := F_e/F_G

Einsetzen ergibt:
E₁ = e² / 4πε₀Gm_nm_e = 2 · e²/4πε₀m_ec²· c²/2Gm_n = 2 r₀/r_G

Wieder liege ich um einen Faktor 2 daneben, den ich vernachlässige.

Beweis von Satz (6):

Der Satz (6) folgt direkt aus (7) und (5).
E₁ / E₁^1/2 = (2 r₀/r_G) : (2 · l_Pl / r_G)
E₁^1/2 = r₀/l_Pl

Diese Beziehung stimmt wieder exakt.

3.3. Veränderung der Gravitationskonstanten?

Die Sätze (1), (2) und (4) können nicht ohne weitere Annahmen bewiesen werden. Sie hängen mit der Ausdehnung und mit den Anzahl Teilchen im Universum zusammen.

(1) R_Universum / r₀ = ca. E₁

(2) T_Universum/ t₀ = ca. E₁

(4a) M_Universum / m_n = ca. E₁²

(4b) Anzahl Nukleonen im Universum = ca. E₁²

Bevor ich mich an einer Erklärung versuche, möchte ich auf einen lehrreichen Irrweg von Paul Dirac hinweisen. Dirac ging wie ich oben von (3) aus und nahm an, alle Gleichungen handeln von der gleichen Zahl E₁. Also:
(3) E₁ := e² / Gm_nm_e
Er nahm an, die grossen Zahlen in den obigen Formeln, die alle um 10⁴⁰ herum liegen, seien alle gleich. Weiter nahm er die Gleichung (2), löste sie nach T auf und erhielt:

T = t₀ · E₁ = e² / (m_e c³) · E₁

(3) einsetzen ergibt:

(9)                   T = (e⁴ / (Gm_e² m_n c³)

Diese Gleichung (9) zeigt ein Problem: Während die Zeit T läuft, also die linke Seite grösser wird, haben wir auf der rechten Seite ausschliesslich Naturkonstanten. Wie kann es sein, dass die Gleichung gilt? Paul Dirac schloss daraus, dass zumindest eine der Konstanten e, G, m_e, m_n oder c nicht konstant sind, sondern sich in der Zeit ändern. Der Aufbau der Materie hängt empfindlich von den Grössen e, m_e, m_n und c ab und auch das Licht, das wir von fernen Sternen sehen und das ja aus einer viel früheren Epoche des Universums stammt, müsste völlig anders aussehen, wenn eine dieser Grössen sich ändern würde. Wenn sich eine von diesen Grössen in den letzten paar Milliarden Jahren auch nur leicht verändert hätte, würde unsere Welt völlig anders aussehen. Eine nahe liegende Annahme ist deshalb, dass sich G(T) proportional zu T^-1 ändert.

Mit dieser Annahme konnte Dirac die Formeln (3), (5), (6), (7) und (8) erklären, allein dadurch, dass G nicht konstant ist, sondern sich mit T^-1 ändert. Mit wenigen, durchaus plausiblen Zusatzannahmen käme man auch auf (1), (2) und (4). Diracs Idee hat also grosse Überzeugungskraft. Die grossen Zahlen beweisen einfach, dass die Gravitationskonstante keine Konstante ist!

So leicht ist es leider nicht. Bei genauer Betrachtung stellt sich heraus, dass ein solches Universum sich dreimal so schnell entwickelt hätte wie das unsrige. Nach Diracs These wäre unser Universum nur wenig älter als unser Sonnensystem. Unsere Sonne ist ein Stern zweiter oder dritter Generation. Bevor sie entstand, müssen andere Sterne entstanden und erloschen sein. Die Sternentwicklung wäre zwar schneller abgelaufen, weil ja die Gravitationskonstante grösser war. Dennoch scheint die Zeit sehr knapp.

Ausserdem wäre die Sonne lange Zeit wesentlich näher bei der Erde gewesen und weil die Leuchtkraft von Sternen von G⁷ abhängt, hätte sie vor 2,5 Mrd. Jahren 128-mal so stark geleuchtet (siehe Har 1). Unter diesen Bedingungen hätte sich das Leben sicher nicht so entwickelt, wie wir es kennen (siehe dazu auch Datierungsmethoden).

Diracs Idee war zwar gut, aber sie wird durch die Beobachtung widerlegt. Man könnte versucht sein, G ein bisschen weniger extrem zu verändern. Aber damit verspielt man sich praktisch die ganze Erklärungskraft.

Wenn aber G sich nicht ändert, müssen wir eine andere Erklärung für die Feinabstimmung finden. Es ist schwer vorstellbar, dass die Gleichung (9) nur gerade heute gilt und sonst in der ganzen Geschichte des Universums falsch war. Einerseits soll also die rechte Seite von (9) konstant sein, andererseits soll die Gleichung doch nicht nur für unsere Zeit gelten: Eine scheinbar paradoxe Fragestellung!

Wir müssen aber wissen, dass das Alter und der Radius des Universums keineswegs direkt gemessen werden kann. Ganz grob gesagt, messen wir, wie schnell sich das Universum heute ausdehnt. Und wir messen von einigen näheren Sternen, wie weit sie heute von uns entfernt sind. Nun ist es so, dass die ferneren Sterne sich schneller von uns wegbewegen als die näheren. Wenn wir diese Bewegungen der Sterne zurückrechnen, erkennen wir, dass sie alle vor etwa 13,5 Milliarden Jahren genau an einem Punkt waren. Um genau zu wissen, wann sie an einem Punkt waren, müssten wir aber nicht nur ihre heutige Geschwindigkeit kennen, sondern auch ihre Beschleunigungen.

Wir haben verschiedene kosmologische Modelle, also begründete Vermutungen, wann sich das Universum wie schnell ausdehnte. Aber bestimmen können wir das Alter des Universums nur unter Annahme eines bestimmten Modells. Ähnliches gilt für den Radius.

Eine mögliche Erklärung für (9) ist deshalb: Die Zeit T_Universum gehört nicht wirklich in diese Gleichung. Es ist nur so, dass über einen grossen Zeitraum der Weltgeschichte die Gleichung (9) fast stimmt, nämlich im Rahmen des sehr ungenau gemessenen Alters T_Universum des Universums. Das könnte etwa so geschehen (Abbildung 1).

Abbildung 1 Beispiel eines kosmologischen Modells, in dem der konstante maximale Radius des Universums Rmax mit dem an sich variablen Radius des Universums verwechselt werden könnte.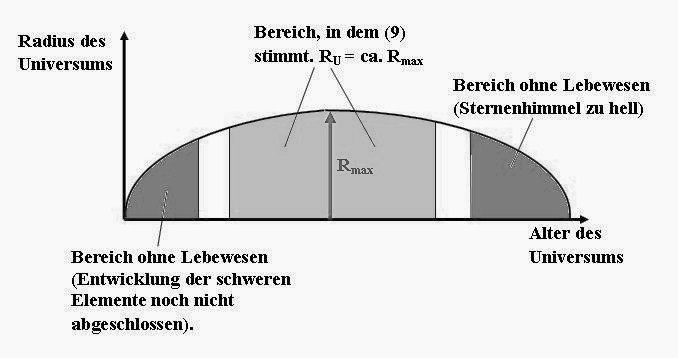

In den Gleichungen (1) und (2) sollten nicht der Radius und das Alter des Universums vorkommen, sondern der maximale Radius R_max des Universums und das dazugehörige Alter. Wir messen zwar den aktuellen Radius und finden eine Feinabstimmung. Dies liegt aber nur daran, dass der aktuelle Radius des Universums nahe bei R_max liegt. Ist dies ein Zufall?

Überhaupt nicht. Ganz am Anfang des Universums lebten noch keine Lebewesen und ganz am Ende können sie nicht mehr existieren (rote Flächen in Abbildung 1). Nach dem anthropischen Prinzip brauchen wir uns also nicht darüber zu wundern, dass wir nicht diese Zeiten beobachten. Während der meisten verbleibenden Zeit ist der Radius des Universums sehr nahe bei R_max, so dass bei der groben Messung und bei einer Toleranz von bis zu Faktor 100 praktisch R_max gemessen wird. Fast alle intelligenten Beobachter, die das Weltall ausmessen, werden eine Feinabstimmung finden.

Ich vermute also, dass nicht der Radius und das Alter des Universums in die Gleichungen zu den Diracschen Zahlen gehören, sondern eine konstante Länge oder Zeit, die für unser Universum charakteristisch ist und die während des Hauptteils der Weltgeschichte praktisch dem Radius oder dem Alter des Universums entspricht.

Ich will als Beispiel, wie eine solche Erklärung aussehen könnte, einmal annehmen, die entscheidende Grösse sei R_max, der maximale Radius des Universums.

3.4. Die kosmischen Zahlen

Es bleiben nach wie vor vier Gleichungen erklärungsbedürftig:

(1) R_max / r₀ = ca. E₁

(2) T_Universum/ t₀ = ca. E₁

(4a) M_Universum / m_n = ca. E₁²

(4b) Anzahl Nukleonen im Universum = ca. E₁²

Auch diese Zahlen schauen nur auf den ersten Blick fremd aus. Sie können aber mit plausiblen Argumenten voneinander abgeleitet werden. Ich zeige nun der Reihe nach, dass (1) und (2) äquivalent sind, und ebenso (4a) und (4b).

Äquivalenz der Sätze (1) und (2)

Die elementare Zeiteinheit t₀ = r₀ / c wird dadurch gebildet, dass ich die elementare Länge r₀ durch c dividiere. Sehr ähnlich erhalte ich auch das Alter des Universums (T_Universum) zumindest der Grösse nach, indem ich den Radius des Universums (R_Universum) durch c dividiere. Das Licht, das gleich nach dem Anfang des Universums ausgesendet wurde, ist während T_Universum mit der Lichtgeschwindigkeit c unterwegs gewesen. Mit dieser vereinfachten Vorstellung kommen wir von der Grössenordnung her auf das richtige Resultat. Die korrekte Beschreibung wäre einiges komplizierter, weil sich der Raum ausdehnt und der heutige Radius des Universums grösser sein kann, als nach der obigen Berechnung. Wieder reicht uns aber die grobe Abschätzung. Es gilt also:

E₁ = R_Universum / r₀ = (R_Universum : c) / (r₀ : c) = T_Universum/ t₀

Äquivalenz der Sätze (4a) und (4b)

Ich habe bereits erwähnt, dass die Masse des Universums zum grossen Teil von den Nukleonen stammt. Auch hier spielt ein Faktor zehn keine Rolle, also auch wenn die Nukleonen nur 1/10 oder gar 1/100 der Masse im Universum ausmachen, so reicht diese Schätzung doch aus, um Diracs Zahlen zumindest plausibel zu machen. Wenn ich also die Masse des Universums durch die Masse eines Nukleons teile, dann erhalte ich in dieser groben Abschätzung die Anzahl Nukleonen.

M_Universum / m_n = Anzahl Nukleonen

Es bleibt zu zeigen, dass (4a) oder (4b) aus (1) folgt.

Aus (1) folgt (4)

Der Satz (4) kann nicht einfach mit einigen Termumformungen bewiesen werden. Er setzt tief greifende Annahmen über das Universum voraus. Es geht darum zu zeigen, dass in einem Universum von bestimmter Grösse eine bestimmte Anzahl Nukleonen enthalten sind. Unser Universum scheint aber ziemlich leer zu sein. Es ist nicht offensichtlich, weshalb nicht viel mehr oder viel weniger Nukleonen in diesem leeren Raum sein können.

In vielen kosmologischen Modellen sieht aber das Universum sehr ähnlich aus wie ein schwarzes Loch. Zum Beispiel im geschlossenen Friedmann-Universum dehnt sich der Raum zuerst aus, erreicht dann einen maximalen Radius R_max und sackt dann von der eigenen Masse zusammengehalten wieder zusammen. Dabei gilt:

R_max = 2GM_Universum/3πc²

Bemerkenswerterweise ist R_max gerade 1/3π des Radius eines schwarzen Loches derselben Masse, ein Faktor 1/3π, der uns angesichts der grossen Zahlen nicht gross zu kümmern braucht.

Ich gehe also von (1) aus und versuche, (4a) zu erhalten:
(1) R_max / r₀ = ca. E₁

Einsetzen ergibt:
E₁ = (2GM_Universum / 3pc²) : (e² / (4pe₀m_e c²)) = (M_Universum/m_n) : (3e² / 8ε₀Gm_nm_e)

Die zweite Klammer auf der linken Seite ist nach (3) in der Grössenordnung von E₁:
(3e² / 8e₀Gm_nm_e) = 3/2 · (e² / 4πε₀Gm_nm_e)

Also:
3/2 · E₁² = (M_Universum/m_n)

Eine wunderschöne Übereinstimmung!

3.5. Die Anzahl Nukleonen im Universum aus mikroskopischen Grössen hergeleitet

Ich habe nun also eine Gruppe von Zahlen aus den Gleichungen (3), (5), (6), (7) und (8), die alle miteinander übereinstimmen und ich kann auch begründen, weshalb sie übereinstimmen müssen. Weiter habe ich eine Gruppe von Zahlen aus den Gleichungen (1), (2), (4a) und (4b), die ebenfalls übereinstimmen, und auch hier weiss ich, woher die Übereinstimmung kommt. In der zweiten Gruppe wird immer eine Grösse aus der Kosmologie mit einer Grösse aus der Teilchenphysik verglichen. In der ersten Gruppe kommen keine Grössen aus der Kosmologie vor.

Ausserdem sehe ich, dass die Zahlen der ersten und der zweiten Gruppe gleich sind, aber ich kenne keinen Grund für diese letzte Übereinstimmung. Ich suche nun also noch einen Zusammenhang zwischen den beiden Gruppen. Die Aufgabe besteht darin, die Anzahl Baryonen im Universum aus den mikroskopischen Grössen Compton-Wellenlänge und Planck-Länge herzuleiten. Wieder verwende ich dazu die Annahme, dass das Universum einem schwarzen Loch gleicht.

Inspiriert von Th. Görnitz (Lyr 1) verwende ich die Formel von Bekenstein und Hawking, die besagt, dass schwarze Löcher eine Entropie S_SL proportional zu ihrer Oberfläche A haben und deshalb strahlen. Die Konstanten, die neben S_SL und A in der Formel vorkommen, sagen nur, dass die Oberfläche in Planckschen Einheiten angegeben wird.
S_SL = Ac³/4Gh
Die Entropie ist der Logarithmus der Anzahl möglicher Zustände eines Systems. Entropie hängt mit der Energie zusammen. Wenn ich einem System Energie zufüge, erhöht sich im Allgemeinen die Anzahl möglicher Zustände. In vielen Systemen entspricht die Entropie der Anzahl Freiheitsgrade, was in grossen Systemen oft praktisch gleich der Anzahl Teilchen ist.

Entropie ist ein Mass für Information. Wenn von vielen Zuständen einer verwirklicht ist, dann enthält dieser Zustand mehr Information, als wenn er nur aus wenigen Zuständen ausgewählt worden wäre. Manchmal ist es möglich, Entropie in Bit zu messen, denn auch Bits sind ein logarithmisches Mass für Information: Mit 4 Bit kann ich z. B. aus 2⁴ =16 Zuständen einen auswählen. Ebenso werde ich 16-mal so viele Zustände haben, wenn ich die Entropie vervierfache.

Görnitz schlägt nun vor, die Entropie bei schwarzen Löchern in Bits anzugeben, und zwar entspricht eine Fläche von einer Plancklänge im Quadrat einem Bit (Lyr 1). Weiter nehme ich an, dass die Entropie des Universums beim maximalen Radius R_Max gerade der Entropie eines schwarzen Loches entspricht. Die Bekenstein-Hawking Formel für die Entropie von schwarzen Löchern und für das Universum bei maximaler Ausdehnung lautet dann:
S_SL = A/4 · (2πc³/Gh) = S_Max

Die Konstanten in der Klammer auf der rechten Seite besagen nur, dass die Oberfläche des schwarzen Loches in Planck-Einheiten ausgemessen wird. Mit der Formel für die Kugeloberfläche:
A=4πR²

und dem Schwarzschildradius:
R = 2GM/c²

erhalte ich:

(10)                 S_Max =: S = 4πG²M²/c² · c³/Gh = 4pGcN²m_p²/h

Im letzten Schritt habe ich die Masse M des Universums als Anzahl Teilchen N mal Protonenmasse m_p geschrieben. Das ist deshalb möglich, weil Protonen und die praktisch gleich schweren Neutronen den Hauptteil der Masse im Universum ausmachen (auch hier spielt ein Faktor 2-10 keine Rolle). Formel (10) zeigt mir also eine Beziehung zwischen der Entropie des Universums und der Anzahl N der Protonen und Neutronen im Universum.

S ist eine Anzahl Bit, also Information. Ich nehme an, diese Information dient dazu, den Aufenthaltsort der Teilchen anzugeben. Ich stelle mir S Ja/Nein Entscheide vor, also S Orte, an denen entweder ein Teilchen ist oder nicht. Wenn diese Teilchen Nukleonen sind, so muss jeder dieser S Plätze das Volumen eines Nukleons haben. Dies ergibt als Gesamtvolumen für das Universum:
V_Max = Sπr₀³ 4/3

S ist eine Anzahl Bit, also Information. Ich nehme an, diese Information dient dazu, den Aufenthaltsort der Teilchen anzugeben. Ich stelle mir S Ja/Nein Entscheide vor, also S Orte, an denen entweder ein Teilchen ist oder nicht. Wenn diese Teilchen Nukleonen sind, so muss jeder dieser S Plätze das Volumen eines Nukleons haben. Dies ergibt als Gesamtvolumen für das Universum:

V_Max = Sπr₀³ 4/3

Unter der Annahme, dass das Universum einem schwarzen Loch gleicht:
4/3 · S_Maxπr₀³= 4/3 · πR³ = 4/3 · π8G³M³/c⁶ = 4/3 · π8G³N³m_p³/c⁶

Wieder erhalte ich eine Beziehung zwischen der Entropie S_Max des Universums und der Anzahl Teilchen darin. Wenn ich nach S auflöse, ergibt sich:

(11)                 S_Max = N³m_p³8G³/c⁶r₀³

(10) und (11) können wir gleich setzten und nach N auflösen:
4πGcN²m_p²/h = N³m_p³8G³/c⁶r₀³
N = 4pc⁵r₀³/m_pG²h = 8,932 · 10⁷⁹

Wir erhalten also in hervorragender Übereinstimmung die Anzahl der Nukleonen im Universum.

4. Allfällige Einwände

4.1. Wieso liefern nur die Nukleonen einen Beitrag zur Entropie?

Es scheint willkürlich, dass in der obigen Betrachtung nur gerade die Nukleonen einen Beitrag zur Entropie leisten. In einer exakten Rechnung müsste man alle Teilchen berücksichtigen. Für eine erste grobe Abschätzung reicht aber der Beitrag der Nukleonen. Die Entropie wird gebraucht, um die Teilchen zu postitionieren. Da die Wellenlänge der Nukleonen kleiner ist als die von Licht oder z. B. Elektronen, brauchen die Nukleonen viel mehr Information, um positioniert zu werden. Die anderen Teilchen würden also in genau gleicher Weise einen Beitrag zur Entropie liefern, aber dieser ist in einer groben Abschätzung vernachlässigbar.

Es ist bemerkenswert, dass in beiden Gleichungen (10) und (11) die Nukleonen dominieren. Denn erstens sind die Nukleonen die massereichsten Teilchen, was für (10) eine Rolle spielt und zweitens haben sie den kleinsten Radius (Comptonwellenlänge), was für (11) wichtig ist. Ich betrachte dies als Hinweis, dass der Zusammenhang zwischen Masse, Ausdehnung und Entropie einigermassen richtig verstanden ist.

4.2. Sinkt die Entropie?

Aufgrund der Gleichungen (10) und (11) könnte man auf die Idee kommen, die Entropie im Universum sinke. Denn wenn die Nukleonen mit der Zeit verstrahlen, müsste da nicht die Entropie abnehmen und schliesslich sogar zu null werden? -Wir reden hier immer von der Entropie beim maximalen Radius des Universums. Ausserdem setze ich voraus, dass ein grosser Teil der Masse und damit auch der Entropie von den Nukleonen stammt. In einem strahlungsdominierten Universum gilt die obige Aussage nicht.

5. Zusammenfassung

Ich denke, mit dieser Darstellung habe ich zumindest plausibel gemacht, dass die Diracschen grossen Zahlen nicht auf reinem Zufall beruhen. Ein grosser Teil der Feinabstimmung liegt in der Tatsache begründet, dass der klassische Elektronenradius gerade von der Grössenordnung der Compton-Wellenlänge des Protons ist. Dieses Zusammentreffen lässt sich mit dem anthropischen Prinzip erklären: Wären Elektronen und Protonen von völlig unterschiedlicher Grösse, so gäbe es keine stabilen Atome, und damit auch keine Lebewesen, die ein solches Universum beobachten.

Die Abstimmung mit den grossen kosmologischen Zahlen (Ausdehnung und Alter des Universums und die Anzahl Nukleonen) können wohl mit einem geeigneten kosmologischen Modell erklärt werden. Wenn wir auf das Universum die Formeln für schwarze Löcher anwenden, dann ergibt sich die Übereinstimmung von selbst. Kosmologische Modelle können daran gemessen werden, wie gut sie Diracs Zahlen erklären.

6. Weiterführende Literatur:

Weitere Artikel auf dieser Homepage:

Anthropisches Prinzip

Buchempfehlungen:

Eine sehr ausführliche Diskussion dieser Zahlen und verschiedener Interpretationen findet man bei Edward R. Harrison, ‚Kosmologie’ (Har 1).

Gute weitere Anregungen für mathematisch Geschulte gibt (Lyr 1), der die Überlegungen zur Entropie mit von Weizsäckers Ur-Theorie in Verbindung bringt.