Das Hamiltonsche Prinzip der kleinsten Wirkung

Visits: 2631

Philipp Wehrli, 7. August 2012

William Rowan Hamilton

Eine Wirkung ist in der Physik eine Grösse mit der Einheit Joule-Sekunden, also Energie mal Zeit oder Impuls mal Weg. Hamiltons Prinzip der kleinsten Wirkung besagt, das ein Teilchen jeweils den Weg geht, bei dem die Wirkung am kleinsten ist. Das Prinzip kann auch in Viel-Teilchen-Systemen angewendet werden, indem die Wirkung aller Teilchen summiert wird. Es spielt eine herausragende Rolle in der Quantenfeldtheorie. Als ich in der Mechanikvorlesung zum ersten Mal von diesem Prinzip hörte, kam es mir wahrhaft magisch vor. Da schien ein Teilchen Informationen aus dem gesamten Universum in komplizierter Weise zu verrechnen, um dann den kürzesten Weg zu wählen. Mitstudenten überlegten sich die abenteuerlichsten Modelle, was diese esoterische ‘Wirkung’ sein mochte. Erst als ich Feynmans wunderbare Erklärung las, verstand ich, dass es sich um ein ganz gewöhnliches Wellenphänomen handelt (Fey 2). (Feynman erwähnt allerdings in seinem Buch den Begriff ‘Hamiltons Prinzip’ nicht.

1. Alle Materie bewegt sich wellenartig

In der Quantentheorie wird jedem Teilchen ein Wellenpaket zugeschrieben und die Frequenz dieser Welle ist proportional zur Energie des Teilchens. Für Photonen gilt die Formel von Einstein:

E = hν,

wobei E die Energie, ν (sprich: “nü”) die Frequenz und h das Plancksche Wirkungsquantum sind. Es ist bemerkenswert, dass diese kurze, absolut revolutionäre und bedeutsame Formel kaum bekannt ist, während die Formel E=mc² von Strassenbuben an die Hausmauern geschrieben wird. Die Formel besagt, dass Photonen als Energiepakete auftreten, also wie Teilchen an genau einem Punkt auftreffen. Gleichzeitig aber haben sie eine Frequenz und bewegen sich wie Wellen über weite Gebiete verschmiert.

Dass etwas gleichzeitig Teilchen- und Welleneigenschaften haben kann, hat die Physiker jahrzehntelang verwirrt und wurde zum Ausgangspunkt der Quantentheorie. Louis de Broglie zeigte später, dass für Materie das Gleiche gilt: Auch Materieteilchen haben eine Frequenz und bewegen sich wie eine Welle, kommen aber immer nur an einem Ort an.

2. Was ist eine Wirkung?

Die Frequenz ν gibt also an, wie oft die Welle in einer Sekunde schwingt. Wir können uns zu jedem Teilchen einen Pfeil vorstellen, der ν Umdrehungen pro Sekunde macht. In der Zeit t macht die Welle tν Schwingungen.

Nun haben wir es in der Natur meist mit sogenannten stehenden Wellen zu tun. Eine Welle ist in einen bestimmten Bereich eingeschlossen, z. B. indem ein Elektron in einem Atom gebunden ist. Wie im Artikel Bohrsches Atommodell gezeigt, bilden sich in dieser Situation eine feste Anzahl Wellenbuckel. In so einem Wellenbuckel kann sich der Pfeil gerade einmal drehen. Deshalb ist die Wirkung gequantelt und h heisst kleinstes Quantum heisst das Plancksche Wirkungsquantum.

3. Wie sich Wellen ausbreiten

Für Wellen gilt das Prinzip von Huygens:
Eine Welle breitet sich so aus, dass jeder Punkt, den sie erreicht, selbst zum Zentrum einer Kugelwelle wird. Die Superposition aller Huygenschen Kugelwellen gibt die Wellenfront zu einem späteren Zeitpunkt.

Abbildung 1 Das Prinzip von Huygens (1629-1695), beschreibt, wie sich Wellen ausbreiten. Eine Welle kann gedacht werden als Überlagerung unzähliger Kugelwellen. Durch Interferenz löschen sich viele Teile gegenseitig aus. Es bleibt eine gemeinsame Wellenfront.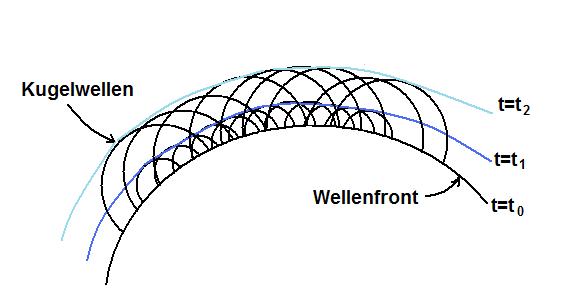

Das Prinzip von Huygens enthält bereits die Grundidee, die auch hinter Richard Feynmans Pfadintegral Methode, die in der Quantenfeldtheorie eine entscheidende Rolle spielt: Wenn jeder Punkt, den die Welle erreicht, als Mittelpunkt einer neuen Welle betrachtet werden kann, kann ich jeden Weg durch den Raum als Weg von Mittelpunkt zu Mittelpunkt zu Mittelpunkt u. s. w. ansehen. Auf diesem Weg dreht sich der in 2. vorgestellte Pfeil stetig weiter.

Um zu sehen, wie weit sich ein Pfeil auf einem bestimmten Weg von A nach B dreht, muss ich die Frequenz n mit der benötigten Zeit t multiplizieren. Bzw., wenn die Drehgeschwindigkeit nicht überall gleich schnell ist, muss ich integrieren.

Um zu sehen, wie hoch die Welle an einem bestimmten Ort A zu einem bestimmten Zeitpunkt ist, muss ich die Pfeile aller möglichen Wege nach A ausrechnen und summieren. Das ist gerade, was wir in der Pfadintegral Methode tun.

Wie weit sich der Pfeil gedreht hat, wird durch die Wirkung S angegeben. Dieses S hat eine enorme Bedeutung in der Quantentheorie.

4. Weshalb ist die Wirkung minimal?

Schauen wir nun an einem einfachen Beispiel, weshalb das ‘Teilchen’ stets den Weg wählt, auf dem die Wirkung minimal ist. Bei Feynman findet man eine ganze Reihe solcher Beispiele (Fey 2).

Betrachten wir die folgende Situation: Eine Lichtquelle steht bei A, ein Beobachter bei B. Der direkte Weg zwischen A und B wird durch einen Schirm versperrt, aber das Licht kann über einen Spiegel zu B gelangen. Wir wissen, dass bei Spiegelungen jeweils der Einfallswinkel gleich dem Ausfallswinkel ist. Aber woher weiss das Licht, welchen Weg es wählen muss?

Abbildung 2 Bei Spiegelungen ist jeweils der Einfallswinkel gleich dem Ausfallswinkel. In der klassischen Mechanik mit Teilchen wird die dadurch erklärt, dass der Impuls senkrecht zum Spiegel beim Aufprall umgekehrt wird. Wenn aber nach der Pfadintegral Methode das Teilchen jeden möglichen Weg geht, funktioniert diese Erklärung nicht mehr.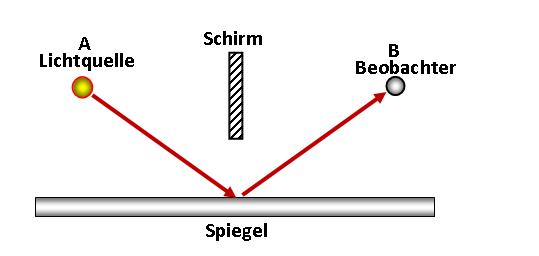

Schauen wir daher die gleiche Situation noch einmal an. Berücksichtigen wir dabei aber, dass die Welle jeden nur möglichen Weg geht. Ich unterteile dazu den Spiegel in viele Stücke. Der Weg kann von A über 1 nach B führen oder über 2 oder über 3 u. s. w.

Damit wir für alle Experimente das richtige Resultat kriegen, müssen in der Rechnung tatsächlich alle diese Wege berücksichtigt werden. Zu jedem Weg gibt es eine Amplitude (einen Pfeil). Alle Amplituden müssen addiert werden. Wie von der Interferenz von Wellen bekannt ist, werden sich diese Amplituden an einigen Orten gegenseitig auslöschen, während sie sich an anderen Orten zu einer besonders hohen Welle auftürmen.

Abbildung 3 Das Prinzip der kleinsten Wirkung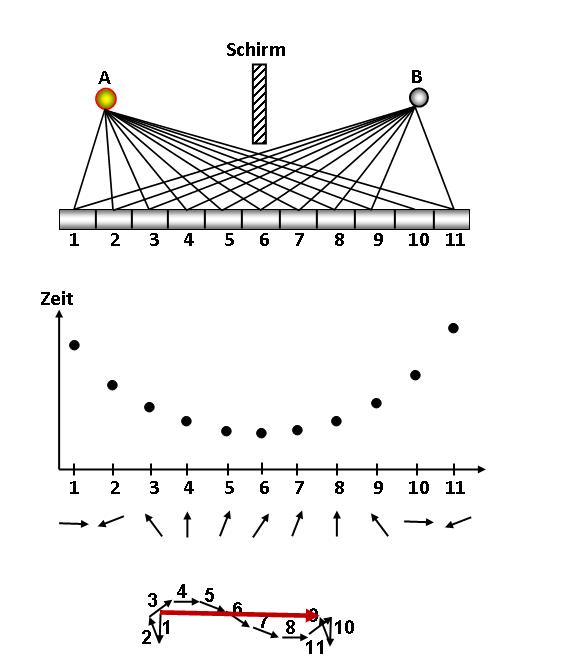

Für das gleiche Beispiel wie in Abbildung 2 sind nun elf Wege eingezeichnet. In Wirklichkeit, müsste man unendlich viele Wege berücksichtigen.

Im Diagramm ist zu jedem darüber liegenden Weg die benötigte Zeit eingezeichnet. Der Zeitunterschied zwischen 5, 6 und 7 ist sehr klein. Deshalb dreht sich der Pfeil praktisch gleich weit, ob er nun den Weg von 5, 6 oder von 7 geht (siehe die eingezeichneten Pfeile unter dem Diagramm). Der Weg 1 ist aber wesentlich länger als 2. Obwohl die Wege nahe beieinander liegen, erhalten wir völlig andere Pfeile.

Die Pfeile aller Wege werden addiert. Dies ergibt den roten Pfeil, die Amplitude der Welle, die bei B ankommt. Obwohl über alle Wege summiert wurde, tragen nur die mittleren Wege wesentlich zum Ergebnis bei.

Wie erwähnt, lehnt sich diese Darstellung eng an Feynman an , auch wenn Feynman den Begriff ‘Hamiltonsches Prinzip der kleinsten Wirkung’ nicht verwendet. Feynman führt dafür eine ganze Reihe schöner Beispiele vor (Fey 2). Was passiert z. B., wenn jeder zweite Weg durch einen Kratzer im Spiegel versperrt wird? Was geschieht, wenn der Pfeil nicht überall gleich schnell dreht, weil das Licht z. B. durch eine dichtere Luftschicht geschickt wird? Was geschieht, wenn mehrere Teilchen im Spiel sind?

5. Kleinste oder grösste Wirkung?

Die Herleitung des Hamiltonschen Prinzips basiert darauf, dass beim Minimum die Steigung der betrachteten Funktion null ist. Wenn nämlich eine Funktion f(x) im Punkt m die Steigung null hat, also f’(m)=0, dann unterscheiden sich Werte der benachbarten Punkte f(m+ε) und f(m-ε) für kleine e nur ganz wenig. Das ist der Grund, weshalb sich die Pfeile zu einem grossen Wert summieren.

Das Gleiche geschieht aber auch bei einem Maximum, bei einem Wechselpunkt oder bei einer konstanten Funktion. Hamiltons Prinzip ist daher ein Extremalprinzip. Ein Teilchen kann auch den längsten Weg wählen. Was der Fall ist, hängt auch von der Wahl der Koordinaten ab. In der Relativitätstheorie kommt man durch die Wahl der Minkowski-Koordinaten auf eine maximale Eigenzeit.

6. Die mathematische Formulierung

a) Klassische Mechanik

Wie wird dies nun mathematisch ausgedrückt? Betrachte dazu Abbildung 3. Zunächst einmal brauchen wir einen Ausdruck, der angibt, wie schnell der Pfeil sich dreht. Dies leistet die sogenannte Lagrange-Funktion
L := T – U
Dabei ist T die kinetische und U die potentielle Energie eines oder mehrerer Teilchen. In der klassischen Mechanik würde man nicht denken, dass dieser Ausdruck mit der Einheit Energie die Drehgeschwindigkeit eines Pfeiles beschreiben könnte. In der Quantentheorie kann aber die Energie als Frequenz ausgedrückt werden.

Man beachte, dass die potentielle Energie mit einem Minuszeichen vorkommt. L ist also nicht die Energie des Teilchens, die erhalten ist. Man kann sich vorstellen, dass T die Drehgeschwindigkeit des Pfeiles des Teilchens ist, während ein Kraftfeld eine zusätzliche Drehung bewirkt, die je nach Ort unterschiedlich stark ist.

L beschreibt also sozusagen die Drehzahl des Pfeiles an einem bestimmten Ort. L hängt von der Zeit t, vom Ort aller beteiligten Teilchen q₁(t),…q_n(t) und von deren Geschwindigkeiten q’₁(t),…q’_n(t) ab. Also:
L(t, q₁(t),…q_n(t) , q’₁(t),…q’_n(t)).
Dabei werden für den Ort und den Impuls nicht die Variablen x und p verwendet, weil es sich um verallgemeinerte Koordinaten handeln kann, etwa um den Winkel und den Drehimpuls eines Pendels.

Um die gesamte Drehung für einen bestimmten Weg zu erhalten, muss man über die benötigte Zeit integrieren. Dies ergibt das äusserst wichtige Wirkungsintegral S(t,q,q’):

Gesucht ist nun derjenige Weg, für den das Wirkungsintegral S(t, q, q’) extremal wird. Wir variieren also die möglichen Wege und suchen einen Weg q(t), für den S(t, q, q’) kleiner wird, als für jeden anderen Weg. Man kann nun zeigen (Heu 1), dass jeder Weg, bei dem dies geschieht, notwendig der Euler-Lagrange Differentialgleichung genügt:

b) In der Quantenfeldtheorie

In der Quantenfeldtheorie gehört die Wirkung S nicht mehr zu einem klassischen Weg q(t), sondern zu einem Feld j(t). Dieses Feld ist über die ganze Raumzeit ausgebreitet, so wie bei der Fourierzerlegung die harmonischen Wellen über die ganze Raumzeit ausgebreitet sind. Deshalb müssen wir über die ganze Raumzeit integrieren:

In der klassischen Physik steht die Lagrangefunktion für die Differenz zwischen kinetischer und potentieller Energie T-U. In der Quantenfeldtheorie sieht dies z. B. so aus (Zee 1):

Nun müssen wir aber über alle möglichen Felder integrieren, so dass wir für ein skalares Feld das sogenannte Pfadintegral Z erhalten:

7. Weiterführende Literatur

Richard P. Feynman, ‘QED – Die seltsame Theorie des Lichts und der Materie’
Das oben mehrfach zitierte Buch von Feynman ist eines der erhellendsten allgemeinverständlichen Bücher zur modernen Physik (Fey 2). Der Entdecker der Pfadintegralmethode erklärt anschaulich, worum es hier geht.

Mathematisch exakter mit den dazu gehörenden Beweisen: (For 2) und (Heu 1)