Kants a priori – Erklärung und Kritik

Visits: 6721

Philipp Wehrli, 27. Dezember 2009, überarbeitet am 8. August 2011

Immanuel Kant

Bei den Betrachtungen auf meiner Homepage gerate ich verschiedentlich in Konflikt mit Kants Erkenntnistheorie, insbesondere in meinen Artikeln zum Induktionsprinzip und zur Relativitätstheorie. Da viele Immanuel Kant in Sachen Erkenntnistheorie immer noch als Autorität schlechthin betrachten, muss ich diese Konflikte näher erläutern. Ich will hier Kants Sicht darstellen und kommentieren. Insgesamt betrachte ich Kants Ansatz als gescheitert, da das a priori Wissen nicht begründet werden kann. Im letzten Abschnitt zeige ich aber doch einen Weg, mit dem eine Physik a priori noch möglich sein könnte, wenn auch auf völlig andere Art, als Kant sich dies dachte.

Inhaltsverzeichnis

1. Das Induktionsproblem als Kants Ausgangspunkt
2. Begriffserklärung
2.1. Die vier Typen von Urteilen
2.1.1. Urteile a priori und Urteile a posteriori
2.1.2. Synthetische und analytische Urteile
2.1.3. Die vier Typen von Urteilen
2.2. Was meint Kant mit synthetisch und analytisch?
2.3. Weshalb ist es für Kant wichtig, dass die Sätze der Mathematik synthetisch sind?
2.3.1. Die Sätze der Mathematik als Präzedenzfall
2.3.2. Sind Kants Beispiele zur Mathematik Urteile a priori?
2.3.3. Ist Kants Geometrie a priori?
3. Kants Argumente
3.1. Die zwei Stämme der Erkenntnis
3.2. Die Argumente zur Mathematik und Geometrie
3.2.1. Wie begründet Kant seine Behauptung, es gebe synthetische Urteile a priori?
3.2.2. Wie sind nach Kant synthetische Urteile a priori möglich?
3.2.3. Sollen Mathematiker, die zwar von der Richtigkeit ihrer geometrischen Sätze überzeugt sind, dennoch an der objektiven Gültigkeit und Anwendung dieser geometrischen Sätze auf die Natur zweifeln?
3.3. Die Argumente zu den Naturwissenschaften
3.3.1. Die Urteilstafel und die Kategorientafel
3.3.2. Von den Kategorien zu den Urteilen a priori
3.3.3. Das Induktionsproblem
3.3.4. Die Kategorien schreiben der Natur die Gesetze vor
4. Eine Reihe von Irrtümern, denen Kant mit seiner Erkenntnistheorie eine Grundlage schafft
4.1. Vorbemerkung zu den Irrtümern
4.2. Behauptungen, die sich durch fragwürdige Definitionen retten lassen
4.3. Behauptungen, die durch die moderne Physik widerlegt sind
4.4. Urteile a priori, die zwar noch nicht widerlegt sind, aber nicht zwingend erscheinen
4.5. Eine andere Interpretation von Kants Apriori
5. Einschätzung von Kants Ideen
6. Wie die Physik a priori aufgebaut werden könnte
6.1. Holger Lyre und C. F. von Weizsäcker
6.2. Was können wir a priori wissen?
6.3. Grundriss einer Physik a priori
7. Weiterführende Literatur

Wer gerne die hier angegebenen Kantzitate im längeren Zusammenhang lesen möchte, kann sie in eine geeignete Suchmaschine eingeben. Weil man die Zitate auf diesem Weg sehr einfach findet und weil die genauen, umständlichen, Angaben den Lesefluss stören, verzichte ich z. T. auf exaktes Zitieren.

1. Das Induktionsproblem als Kants Ausgangspunkt

Kants Überlegungen zur Erkenntnistheorie sind inspiriert von David Humes Analyse des Induktionsproblems. Hume stellte fest, dass wir auch mit noch so vielen Erfahrungen nie auf ein Naturgesetz Kausalität schliessen können.

Kant schreibt dazu in den Prolegomena §5 S. 33: „Denn, wie ist es möglich, sagte der scharfsinnige Mann: dass, wenn mir ein Begriff gegeben ist, ich über denselben hinausgehen, und einen anderen damit verknüpfen kann, der in jenem gar nicht enthalten ist, und zwar so, als wenn dieser notwendig zu jenem gehöre? Nur Erfahrung kann uns solche Verknüpfungen an die Hand geben, (so schloss er aus jener Schwierigkeit, die er vor Unmöglichkeit hielt) …“

Hume war sich bewusst, dass er auch mit noch so vielen Erfahrungen nie eine absolute Sicherheit erhalten könnte, was in Zukunft passieren wird. Aufgrund dieser Überlegungen wurde Hume zum Skeptiker und bezweifelte alles. Was wir über die Natur zu wissen glauben, wissen wir nie mit Sicherheit. Letztlich wissen wir nichts über die Natur.

Kant übernahm Humes Argument, lehnte aber die Schlussfolgerung ab. Er kehrte die ganze Sichtweise um und sagte etwa: Durch Erfahrungen können wir das Kausalitätsgesetz nicht sicher begründen. Dennoch wissen wir, dass es gilt. Kant versuchte daher zu ergründen, wie wir das wissen können.

Ausserdem erweiterte er Humes Feststellung auf andere Naturgesetze. Wieder erklärte er, gewisse Urteile seien unbezweifelbar wahr, unabhängig von allen Erfahrungen. Kant nannte diese Urteile a priori. Auf diesen Urteilen a priori könne weitere sichere Erkenntnis aufgebaut werden.

Im Gegensatz zum Skeptiker Hume behauptete Kant also, wir seien durchaus zu absolut gesicherten Urteilen fähig. Um dies zu begründen, untersuchte er zunächst einmal sehr sorgfältig, welche Arten von Urteilen es gibt.

2. Begriffserklärung

2.1. Die vier Typen von Urteilen

Ich halte mich bei den folgenden Definitionen so nahe wie möglich an Kants Wortlaut, versuche aber doch, die nötige Klarheit zu erreichen, damit die Begriffe auch benutzbar werden. Es ist nicht sinnvoll, Kants Definitionen im Wortlaut anzugeben, weil in den Originaltexten kaum sichtbar ist, wo eine Definition anfängt und wo sie aufhört. Was Kant unter den Begriffen genau versteht, wird oft erst an den Beispielen klar. Den Originaltext zu den folgenden Begriffen findet man in der Kritik der reinen Vernunft in der Einleitung.

2.1.1. Urteile a priori und Urteile a posteriori

a priori heisst ein Urteil dann, wenn es unabhängig von jeder Erfahrung ist, also weder durch Erfahrungen begründet wird, noch durch Erfahrungen widerlegt werden kann.

A priori Urteile sind notwendig, sie können also nicht falsch sein, und sie gelten ohne Ausnahme. Beispiele für Urteile a priori sind die Sätze der Mathematik und der Geometrie.

a posteriori heisst ein Urteil, wenn es sich auf Erfahrungen stützt.

A posteriori ist die Feststellung: Wenn ich die heisse Herdplatte berühre, verbrenne ich mich. Dies ist eine Feststellung, wie es bisher war und wie die Welt zu sein scheint. Ich habe diese Regel gelernt, weiss aber nicht, ob es nicht auch Ausnahmen von dieser Regel gibt.

Anmerkung: Unter ‚a priori‘ ist nicht zeitlich vor der Erfahrung zu verstehen. Kant schreibt dazu (Kritik der reinen Vernunft, Einleitung): „Dass alle unsere Erkenntnis mit der Erfahrung anfange, daran ist gar keine Zweifel; denn wodurch sollte das Erkenntnisvermögen sonst zur Ausübung erweckt werden, geschähe es nicht durch Gegenstände, die unsere Sinne rühren? … Der Zeit nach geht also keine Erkenntnis in uns vor der Erfahrung vorher, und mit dieser fängt alle an. … Wenn aber gleich alle unsere Erkenntnis m i t der Erfahrung anhebt, so entspringt sie darum doch nicht eben alle a u s der Erfahrung. Denn es könnte wohl sein, dass selbst unsere Erfahrungserkenntnis ein Zusammengesetztes aus dem sei, was wir durch Eindrücke empfangen, und dem, was unser eigenes Erkenntnisvermögen (durch sinnliche Eindrücke bloss veranlasst, ) auf sich selbst hergibt, …“

2.1.2. Synthetische und analytische Urteile

Weiter unterschied Kant zwischen synthetischen und analytischen Urteilen.

Analytische Urteile sind Urteile, die „bloss erläuternd sind und zum Inhalte der Erkenntnis nichts hinzutun.“ (Prolegomena § 2, S. 18).

Synthetische Urteile sind erweiternde Urteile, welche die Erkenntnis vergrössern (Prolegomena § 2, S. 18).

2.1.3. Die vier Typen von Urteilen

Es sind vier Kombinationen, also vier verschiedene Typen von Urteilen möglich:

Tabelle 1. Vier Typen von Urteilen

	a priori	a posteriori
analytisch	Tautologien, Logik: „Ein Junggeselle ist ein Mann.“	Logisch nicht möglich —
synthetisch	???	Empirisch durch Induktion: „Wenn ich die heisse Herdplatte berühre, verbrenne ich mich.“

Kant wollte zeigen, dass es synthetische Urteile a priori gibt und dass insbesondere das Kausalitätsgesetz, das Hume vergebens zu beweisen versucht hatte, ein synthetisches Urteil a priori ist. Dann nämlich wäre das Kausalitätsgesetz unbezweifelbar wahr und auf dieser Grundlage wären auch Schlüsse von der Erfahrung auf zukünftige Ereignisse möglich.

Der folgende Abschnitt zeigt, dass Kants Begriffe mit Vorsicht zu lesen sind.

2.2. Was meint Kant mit synthetisch und analytisch?

Wer nach den obigen Definitionen glaubt, er habe verstanden, was Kant mit analytisch und synthetisch meint, kann wohl durchaus noch überrascht werden. Kant nannte nämlich z. B. alle mathematischen Sätze synthetisch. Dagegen würden die meisten Mathematiker heute sagen, die Sätze der Mathematik seien analytisch.

Dies kann auf zwei Arten interpretiert werden. Erstens könnte man sagen, für Kant war ‚analytisch‘ ein wesentlich strengeres Kriterium als für die heutigen Mathematiker. Zweitens könnte man sagen, zu Kants Zeit sei die Mathematik tatsächlich synthetisch gewesen. Seither sei sie präzisiert worden und heute sei sie analytisch.

Kant betonte also, die Sätze der Mathematik und der Geometrie seien insgesamt synthetisch. Als Begründung für diese Behauptung, nannte Kant ein Beispiel, nämlich die Gleichung 5+7=12. Er begründete seine Ansicht wie folgt:

KrdrV, Einleitung V.1. Mathematische Urteile sind insgesamt synthetisch S. 64:
„Man sollte anfänglich zwar denken daß der Satz 7+5=12 ein bloß analytischer Satz sei, der aus dem Begriffe einer Summe von Sieben und Fünf nach dem Satze des Widerspruches erfolge. Allein, wenn man es näher betrachtet, so findet man, daß der Begriff der Summe von 7 und 5 nichts weiter enthalte, als die Vereinigung beider Zahlen in eine einzige, wodurch ganz und gar nicht gedacht wird, welches diese einzige Zahl sei, die beide zusammenfaßt. Der Begriff von Zwölf ist keinesweges dadurch schon gedacht, daß ich mir bloß jene Vereinigung von Sieben und Fünf denke, und, ich mag meinen Begriff von einer solchen möglichen Summe noch so lange zergliedern, so werde ich doch darin die Zwölf nicht antreffen. Man muß über diese Begriffe hinausgehen, indem man die Anschauung zu Hülfe nimmt, die einem von beiden korrespondiert, etwa seine fünf Finger, oder (wie Segner in seiner Arithmetik) fünf Punkte, und so nach und nach die Einheiten der in der Anschauung gegebenen Fünf zu dem Begriffe der Sieben hinzutut. Denn ich nehme zuerst die Zahl 7, und, indem ich für den Begriff der 5 die Finger meiner Hand als Anschauung zu Hülfe nehme, so tue ich die Einheiten, die ich vorher zusammennahm, um die Zahl 5 auszumachen, nun an jenem meinem Bilde nach und nach zur Zahl 7, und sehe so die Zahl 12 entspringen. Daß 7 zu 5 hinzugetan werden sollten, habe ich zwar in dem Begriff einer Summe = 7+5 gedacht, aber nicht, daß diese Summe der Zahl 12 gleich sei. Der arithmetische Satz ist also jederzeit synthetisch; welches man desto deutlicher inne wird, wenn man etwas größere Zahlen nimmt, da es denn klar einleuchtet, daß, wir möchten unsere Begriffe drehen und wenden, wie wir wollen, wir, ohne die Anschauung zu Hülfe zu nehmen, vermittelst der bloßen Zergliederung unserer Begriffe die Summe niemals finden könnten.“

In der heutigen Mathematik nehmen die Definitionen keinen Bezug auf Dinge aus der Natur, wie etwa Finger. 5 würde man heute etwa definieren als:

1 + 1 + 1 + 1 + 1

7 ist definiert als:

1 + 1 + 1 + 1 + 1 + 1 + 1

Und addieren ist z. B. definiert als das Aneinandersetzen zweier wie oben definierter Zahlen, wobei ein + dazwischen gesetzt wird. Um zu beweisen, dass 7+5=12 ist, muss ich also zeigen, dass:

1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
=
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

Das folgt aber sogleich aus der Definition des Gleichheitszeichens.

Ich muss also keine Vorstellung von 12 haben, um diese Rechnung auszuführen. Auch ein Taschenrechner könnte das obwohl ihm niemand die Bedeutung sämtlicher möglicher Zahlen eingegeben hat. Was in mathematischen Sätzen festgestellt wird, ist vollständig in den Axiomen und Definitionen enthalten. Dem Beweisführenden ist es nicht erlaubt, weitere Annahmen zu verwenden.

Damit ist natürlich Kants Behauptung, mathematische Sätze seien synthetisch, nicht widerlegt. Das Beispiel zeigt aber, dass wir die Begriffe sorgfältig durchleuchten müssen. Denn wenn wir unter ‚Mathematik‘ die heutige Mathematik verstehen und den Begriff ‚synthetisch‘ leichtfertig verwenden, dann stimmt Kants Behauptung nicht.

Dies wird deutlich, wenn wir den Begriff der ‚Information‘einführen. ‚Information‘ kann auf unterschiedliche Weise definiert werden, aber alle Definitionen laufen darauf hinaus, dass von mehreren Möglichkeiten eine oder mehrere, aber nicht alle, ausgewählt werden.

Beispiel: Vor dem Würfeln habe ich keine Information, welche Zahl kommen wird. Es gibt sechs Möglichkeiten. Wenn ich aber den gefallenen Würfel gesehen habe, habe ich Information, denn von den sechs Möglichkeiten, bleibt nur eine einzige. Wenn jemand anders den Würfel sieht und mir sagt, eine ungerade Zahl liege oben, dann hätte ich ebenfalls Information. Denn nun kämen statt sechs nur noch drei Möglichkeiten in Frage.

Spontan könnte man ein Urteil analytisch nennen, wenn keine Information gebraucht wird, die nicht schon in den Prämissen steckt. Anders ausgedrückt: Es gibt nur eine Möglichkeit, wie das Urteil ausfallen wird. Wenn zwei Mathematiker 5+7 berechnen und keinen Fehler machen, werden sie beide 12 erhalten. Sie haben keinen Spielraum, etwas Persönliches hinzuzufügen. Auch ein Taschenrechner kommt auf dieses Resultat. Deshalb enthält das Resultat 12 keine Information, die nicht schon in den Axiomen und in der Summe 5+7 steckt.

Nach Kant ist aber der Satz 5+7=12 synthetisch! Mit dem Begriff der Information haben wir zwei Möglichkeiten, diese Behauptung zu interpretieren.

Erste mögliche Interpretation: Wenn Kant ein Urteil synthetisch nennt, heisst dies nicht, dass bei der Synthese neue Information hinzugefügt wurde oder entstanden ist. Die Erkenntnis vergrössern bedeutet bei Kant nicht, danach mehr Information zu besitzen!

Zweite mögliche Interpretation: Mathematik war zu Kants Zeit synthetisch, heute ist sie analytisch.

Nach beiden Sichtweisen ist Kants Behauptung richtig. Die Behauptung ist aber falsch, wenn wir unter ‚Mathematik‘ die moderne Mathematik verstehen und mit ‚synthetisch‘ meinen, dass in der Schlussfolgerung Information enthalten ist, die nicht schon in den Prämissen steckt. Es ist wichtig, diese Einschränkung zu kennen, wenn wir Kants Schlussfolgerungen anschauen. Insbesondere müssen wir uns bewusst sein, dass das Beispiel der Mathematik nach beiden Interpretationen für Kants weitere Zwecke unbrauchbar wird.

2.3. Weshalb ist es für Kant wichtig, dass die Sätze der Mathematik synthetisch sind?

2.3.1. Die Sätze der Mathematik als Präzedenzfall

Dass die Sätze der Mathematik und der Geometrie synthetisch sind, ist ein bedeutendes Argument in Kants Überlegung. Denn die Sätze der Mathematik und der Geometrie sind ja offensichtlich a priori, also unabhängig von der Erfahrung. Gleichzeitig sind die Sätze als Urteile a priori auch mit Sicherheit wahr. Das obige Beispiel zeigt also nach Kant, dass synthetische Urteile a priori möglich sind: Wir können ohne sinnliche Erfahrungen durch reines Nachdenken unsere Erkenntnis vergrössern! Da dies aber grundsätzlich möglich ist, besteht berechtigte Hoffnung, dass es auch auf dem Gebiet der Metaphysik gelingt. Kant dazu (Prolegomena, § 2 S. 23):

„So war es doch, als ob er [Hume] gesagt hätte: reine Mathematik enthält bloss analytische Sätze, Metaphysik aber synthetische a priori. Nun irrete er hierin gar sehr, und dieser Irrtum hatte auf seinen ganzen Begriff entscheidend nachteilige Folgen. Denn wäre das von ihm nicht geschehen, so hätte er seine Frage, wegen des Ursprungs unserer synthetischen Urteile, weit über seinen metaphysischen Begriff der Kausalität erweitert, und sie auch auf die Möglichkeit der Mathematik a priori ausgedehnt; denn diese musste er ebenso wohl vor synthetisch annehmen. Alsdenn aber hätte er seine metaphysische Sätze keineswegs auf blosse Erfahrung gründen können, weil er sonst die Axiomen der reinen Mathematik ebenfalls der Erfahrung unterworfen haben würde, welches zu tun er viel zu einsehend war. Die gute Gesellschaft, worin Metaphysik alsdenn zu stehen gekommen wäre, hätte sie wider die Gefahr einer schnöden Misshandlung gesichert, denn die Streiche welche der letzteren zugedacht waren, hätten die erstere auch treffen müssen, …“

Dazu ist zunächst einmal festzuhalten: Kant lag natürlich völlig falsch mit der Behauptung, Hume irrte. Hume hatte einfach eine modernere Sicht, was die Definitionen von ‚Mathematik‘ und ‚synthetisch‘ betrifft. Nach den modernen Definitionen ist Mathematik nicht synthetisch, wie Hume völlig richtig erkannte.

Kant beklagte, dass Hume wegen seiner Sicht nicht bemerkte, dass es synthetische Sätze a priori gibt. Denn dies ist der Schlüsselsatz in Kants Erkenntnistheorie. Kant will am Beispiel der Mathematik zeigen, dass es synthetische Urteile a priori gibt, und er sieht dies als starke Motivation für die Behauptung, dass es auch in der Physik synthetische Urteile a priori gibt.

Kant verwendet also die Sätze der Mathematik als Präzedenzfall für synthetische Urteile a priori. Sind sie das? – Folgen wir einmal Kant in seiner Behauptung, mathematische Sätze seien synthetisch. Wir haben gesehen, dass dies nur möglich ist, wenn wir entweder den Begriff ‚Mathematik‘ oder den Begriff ‚synthetisch‘ modifizieren. Wenn wir aber die Begriffe modifizieren, stellt sich die Frage: Sind die Sätze der Mathematik nach dieser Modifikation immer noch a priori?

2.3.2. Sind Kants Beispiele zur Mathematik Urteile a priori?

Die moderne Mathematik kann wohl a priori genannt werden, denn sie beruht nicht auf Erfahrungen. Die Sätze der modernen Mathematik sind aber sicher nicht synthetisch in dem Sinne, dass beim Schlussfolgern Information gewonnen wird, die nicht schon in den Prämissen steckte. Die moderne Mathematik ist also sicher kein Beleg dafür, dass synthetische Urteile a priori möglich sind.

Da Kant aber mit ‚Mathematik‘ etwas anderes meinte als wir heute, müssen wir seinen Begriff benützen, wenn wir seine Behauptungen beurteilen. Es stellt sich daher die Frage, ob Mathematik, so wie Kant sie verstand, überhaupt a priori ist.

Betrachten wir noch einmal Kants Beispiel 5+7=12. Die meisten Nichtmathematiker denken, es sei a priori völlig klar, wie gezählt und wie addiert werden muss. Mathematikstudenten lernen aber im Grundstudium, dass die Addition auf verschiedene Arten definiert werden kann. Eine Addition ist zunächst einfach eine Abbildung, die jeweils zwei Elementen einer Menge ein drittes zuordnet. Es muss sogar definiert werden, ob a+b=b+a ist. Denn es sind durchaus Definitionen denkbar, bei denen dies nicht der Fall ist.

Dieses Problem erklärt Bertrand Russell sehr ausführlich in ‘Einführung in die mathematische Philosophie’, Vorwort von Michael Otte, Zitat von Russell: In der axiomatischen Grundlegung der Arithmetik „wurde vorausgesetzt, dass wir nicht zu wissen brauchen, was wir unter Null, Zahl und Nachfolger zu verstehen haben, sofern wir nur irgend etwas darunter verstehen, was den fünf Axiomen [von Peano] genügt. Aber dann zeigt es sich, dass es eine unendliche Anzahl möglicher Deutungen gibt. Es möge z. B. 0 das bedeuten, was wir gewöhnlich als 1 bezeichnen, und es möge Zahl das bedeuten, was für gewöhnlich als natürliche Zahl ausser 0 bezeichnen. Dann sind alle fünf Axiome auch richtig, und die gesamte Arithmetik kann bewiesen werden, obwohl jede Formel eine ungewöhnliche Bedeutung hat. 2 bedeutet das, was wir gewöhnlich als 3 bezeichnen. Aber 2+2 bedeutet nicht etwa 3+3, sondern 3+2 … Solange wir im Gebiet der arithmetischen Formen bleiben, sind alle diese Deutungen des Begriffs Zahl gleich gut.“

Mathematiker lösen dieses Problem, indem sie Mathematik in einem völlig abstrakten Bereich betreiben. In diesem Bereich können sie mit absoluter Sicherheit ihre Schlüsse ziehen, die für ganz bestimmte Elemente dieses abstrakten Bereichs gelten. Wenn ein Mathematiker aber eine Aussage über die Natur machen soll, z. B. wie viele Finger man erhält, wenn man 5 Finger und 7 Finger zusammen zählt, dann muss der Mathematiker zuerst beweisen, dass das Zusammenzählen von Fingern nach den gleichen Gesetzen funktioniert wie die Addition von Zahlen in der Mathematik. Ob Finger sich an die Gesetze der Mathematik halten, können wir nur aus unserer Erfahrung wissen.

Wenn Kant also die Addition mit Fingerabzählen erklärt, müssen wir vorsichtig sein. Finger abzählen ist empirisch! Hätte Kant Wassertropfen abgezählt, wäre keineswegs so klar, ob fünf Wassertropfen plus sieben Wassertropfen zwölf Wassertropfen ergibt. Bei Bakterien könnte sich auch ein Problem ergeben, wenn sich diese plötzlich teilen. Wenn ich 5dl Wasser und 7dl Alkohol zusammenmische, ergibt dies weniger als 12dl Flüssigkeit. In der Relativitätstheorie können Massen und Geschwindigkeiten nicht so addiert werden, wie wir dies gewöhnt sind.

Alle diese Beispiele zeigen: Irgendwoher müssen wir die Information haben, was addieren bedeutet. Wir können dies entweder durch Erfahrung lernen, dann sind die Sätze der Mathematik aber nicht mehr a priori. Oder wir können die Begriffe der Mathematik so exakt definieren, dass gar kein Spielraum für andere Resultate bei der Addition mehr besteht. Dann steckt die Information aber vollständig in den Axiomen und Definitionen. Es ist dann fragwürdig, die Sätze der Mathematik synthetisch zu nennen.

2.3.3. Ist Kants Geometrie a priori?

Die obigen Vorbehalte gelten für den ganzen Abschnitt ‚wie ist reine Mathematik möglich‘ in den Prolegomena und die analogen Kapitel in der Kritik der reinen Vernunft. Insbesondere gelten sie auch für Kants Beispiele aus der Geometrie. Kant nimmt als gesichert an, dass wir beim Vermessen unseres Universums nichts anderes finden können, als was wir nach der euklidschen Geometrie erwarten. Kant glaubt, er könne aus den Sätzen der Mathematik und der Geometrie ohne Einschränkung auf den Raum und die Zeit schliessen.

Kant dazu in Prolegomena Erster Teil, Wie ist reine Mathematik möglich? §10: „Geometrie legt die reine Anschauung des Raums zum Grunde. Arithmetik bringt selbst ihre Zahlbegriffe durch sukzessive Hinzusetzung der Einheiten in der Zeit zu Stande, vornehmlich aber reine Mechanik kann ihre Begriffe von Bewegung nur vermittelst der Vorstellung der Zeit zu Stande bringen.“

Wenn Kant die Beschreibung von Raum und Zeit zur Mathematik zählt, müssen wir fragen: Können die so konstruierten Sätze überhaupt a priori sein? Und falls ja, woher wissen wir das dieser Raum und diese Zeit etwas mit unserem Raum und unserer Zeit zu tun haben? – Jedenfalls versteht Kant unter Mathematik etwas so völlig anderes als die Mathematiker heute, dass wir sehr genau darauf achten müssen, wie er seine Schlüsse begründet. Es ist bis hier durchaus nicht klar, ob Kants Beispiele zur Mathematik a priori sind.

Nachdem ich die Problematik der Begriffe aufgezeigt habe, wird es Zeit, einen Überblick über Kants Argumentation zu geben. Dabei wird auch klar werden, dass Kant unter Raum und Zeit etwas grundsätzlich anderes verstand als die Physiker heute. Es wäre deshalb völlig falsch, jetzt von Kant einzelne Aussagen über Raum und Zeit zu zitieren und dann zu zeigen, dass Raum und Zeit in der modernen Physik anders sind. Sie sind anders! – Aber das widerlegt Kant in keiner Weise. Denn über das, was die Physiker heute Raum und Zeit nennen, wollte sich Kant gar nicht äussern.

3. Kants Argumente

3.1. Die zwei Stämme der Erkenntnis

Kant unterscheidet zwei Stämme der menschlichen Erkenntnis, nämlich die Sinnlichkeit und den Verstand. Aus diesen zwei Stämmen ergeben sich zwei Sorten von synthetischen Urteilen a priori. Nämlich erstens also Urteile a priori, welche zur Wahrnehmung von Sinnesreizen notwendig sind, die reinen Anschauungen. Damit wir Sinnesreize überhaupt einordnen können, benötigen wir nach Kant a priori eine Vorstellung von Raum und Zeit. Diese reinen Anschauungen finden wir in der Geometrie (Raum) und der Mathematik (Zeit).

Zweitens gibt es Urteile a priori, die für den Verstand notwendig sind, die reinen Verstandesbegriffe. Diese finden wir in der Logik, nämlich in der weiter unten beschriebenen Kategorientafel. Damit wir in Begriffen denken können, müssen uns die Kategorien a priori gegeben sein.

Tabelle 2. Überblick über die zwei Stämme der Erkenntnis

Sinnlichkeit	Verstand
Sinnesreize strömen in uns hinein und werden nach vorgegebenen Kriterien geordnet.Wir sind passiv.	Wir denken in Begriffen. Wir sind aktiv.
Voraussetzung: Die Gesetze von Raum und Zeit sind uns a priori gegeben durch die Sätze der Geometrie und der Mathematik	Voraussetzung: Die Kategorien sind uns a priori gegeben durch die Sätze der Logik
Behandelt in der transzendentalen Ästhetik	Behandelt in der transzendentalen Logik

 

Allerdings entsteht Erkenntnis erst, wenn sich Sinnlichkeit und Verstand vereinen. Kant fasst dies auf die kurze Formel: „Gedanken ohne Inhalt sind leer, Anschauungen ohne Begriffe sind blind.“

So entsteht durch die blosse Aufnahme von Sinnesreizen keine Erkenntnis. Erst wenn die Sinnlichkeit geordnet ist und wir sie in Begriffe fassen, entsteht Erkenntnis.

Kant behauptete, er habe gezeigt, dass es synthetische Urteile a priori gebe. Nach den obigen Bemerkung sind dabei zwei Arten zu unterscheiden, nämlich, diejenigen, welche eine Voraussetzung der Sinnlichkeit sind, und denjenigen, die eine Voraussetzung des Verstandes sind. Die Argumentation zu diesen beiden Arten unterscheidet sich leicht. Ich will sie in den Abschnitten 3.2. und 3.3 diskutieren.

3.2. Die Argumente zur Mathematik und Geometrie

3.2.1. Wie begründet Kant seine Behauptung, es gebe synthetische Urteile a priori?

Kant betont, dass wir über die Dinge an sich, also über die Realität, a priori nichts aussagen können. Notwendig a priori sind die Dinge nur als Gegenstände der Erfahrung. Raum und Zeit sind nach Kant nicht Dinge an sich, sondern Ordnungsschemata, nach denen wir unsere Sinneswahrnehmungen ordnen. Er begründet diese Behauptung wie folgt:

Prolegomena Erster Teil, Wie ist reine Mathematik möglich? §10:
„Beide Vorstellungen [Raum und Zeit] aber sind bloß Anschauungen, denn wenn man von den empirischen Anschauungen der Körper und ihrer Veränderungen (Bewegung) alles Empirische, nämlich was zur Empfindung gehört, wegläßt, so bleiben noch Raum und Zeit übrig, welche also reine Anschauungen sind, die jenen a priori zum Grunde liegen, und daher selbst niemals weggelassen werden können, aber eben dadurch, daß sie reine Anschauungen a priori sind, beweisen, daß sie bloße Formen unserer Sinnlichkeit sind, die vor aller empirischen Anschauung, d.i. der Wahrnehmung wirklicher Gegenstände, vorhergehen müssen, und denen gemäß Gegenstände a priori erkannt werden können, aber freilich nur, wie sie uns erscheinen.“

Man beachte, dass Kant den entscheidenden Punkt, nämlich dass Raum und Zeit a priori gegeben sind, einfach voraussetzt, etwa: “Wenn wir alles Empirische weglassen, bleiben Raum und Zeit.“ Kant setzt voraus, dass Raum und Zeit nichts Empirisches sind, denn sonst könnten wir sie ja auch weglassen.

Man könnte auch sagen: Kant definiert die Begriffe Raum und Zeit anders, nämlich als Formen, nach denen wir unsere Sinnlichkeit ordnen. Die Geometrie beschreibt den Raum und gibt damit den Rahmen vor, in den wir unsere Sinnesreize ordnen. Der Raum und die Zeit sind nach Kant nicht eine Bühne, auf der sich die Dinge an sich bewegen, sondern sie sind Formen, denen sich unsere Sinnesreize anpassen müssen. Kant meint also etwas grundsätzlich anderes mit ‚Raum‘ und ‚Zeit‘ als die Physiker, die sagen würden: „In der Realität gibt es Raum und Zeit“ oder zumindest: „Physikalische Objekte – also Dinge an sich – bewegen sich durch Raum und Zeit.“

Es ist unsinnig, darüber zu diskutieren, ob Kant oder die Physiker recht haben mit ihrer Ansicht, was „Raum“ und „Zeit“ seien. Hier handelt es sich um unterschiedliche Definitionen, die nicht falsch sein können. Sie können höchsten nützlich oder umständlich oder irreführend sein, aber nicht falsch.

Wenn wir etwas wahrnehmen, dann nehmen wir also nicht das Ding an sich wahr, sondern nur dessen Erscheinung, also das Abbild, das unsere Sinne zulässt. In einem modernen Bildnis können wir uns vorstellen, alle Bilder unserer Umwelt kämen nur über eine Digitalkamera zu uns. Wir sehen also die Welt an sich nicht vollständig und auch nicht korrekt, sondern wir erhalten auf einen Mikrochip gespeichert eine Reihe von Nullen und Einsen, und zwar in einer Anordnung, die mit der Realität nur sehr indirekt etwas gemeinsam hat. Wenn ich nun in dieser Weise alle Sinnesreize gepixelt wahrnehme und gepixelt verarbeite, wäre es unmöglich, anderes wahrzunehmen als gepixelte Bilder.

Die Gesetze der Pixelung könnte ich aber a priori kennen, denn sie sind ja in mir drin, Gesetze meiner eigenen Sinne. Ich kann auch a priori schliessen, dass alle weiteren Bilder mir ebenfalls nur gepixelt erscheinen können, völlig unabhängig davon, was in der Welt an sich vor sich geht.

In diesem Sinne erklärt sich Kant, wie wir a priori unumstössliches Wissen davon haben können, was in unseren Anschauungen passieren kann und was mit Sicherheit nicht. Der euklidische Raum und die Newtonsche Zeit bilden den Rahmen, in den die Reize der Aussenwelt eingepasst werden, bevor wir sie wahrnehmen. Wir können uns absolut darauf verlassen, dass wir nie einen Sinnesreiz empfangen, der nicht in diesen Rahmen passt, völlig unabhängig davon, wie die Welt an sich sein mag.

Nach diesem Bild sind es nicht die Dinge an sich, die unsere Wahrnehmung ausmachen, sondern es ist der durch unsere Sinne eingeschränkte Rahmen, dem sich die Wahrnehmungen anpassen müssen. Diesen entscheidenden Perspektivenwechsel verglich Kant mit der Kopernikanischen Wende. Kant dazu:

„Bisher nahm man an, alle unsere Erkenntnis müsse sich nach den Gegenständen richten; aber alle Versuche über sie a priori etwas durch Begriffe auszumachen, wodurch unsere Erkenntnis erweitert würde, gingen unter dieser Voraussetzung zunichte. Man versuche es daher einmal, ob wir nicht in den Aufgaben der Metaphysik damit besser fortkommen, daß wir annehmen, die Gegenstände müssen sich nach unserem Erkenntnis richten, welches so schon besser mit der verlangten Möglichkeit einer Erkenntnis derselben a priori zusammenstimmt, die über Gegenstände, ehe sie uns gegeben werden, etwas festsetzen soll.“ Kant, Immanuel: Kritik der reinen Vernunft. Vorrede zur zweiten Ausgabe.

Ich habe oben Kants Argumentation in meinen Worten zusammen gefasst, möchte aber zum Beleg eine Textstelle aus den Prolegomena zitieren. Kant hat diesen Text ohne Abschnitte und ohne Hervorhebungen verfasst. Ich denke, der Leser wird nicht unglücklich sein, wenn ich Abschnitte hinzufüge. Ausserdem numeriere ich die Abschnitte, weil ich sie einzeln kommentieren möchte. Insbesondere werde ich diskutieren, ob Kant nun tatsächlich bewiesen hat, dass synthetische Sätze a priori möglich seien.

3.2.2. Wie sind nach Kant synthetische Urteile a priori möglich?

Kant, Prolegomena Erster Teil Anmerkung I:	Mein Kommentar:
(i) „Die Sinnlichkeit, deren Form die Geometrie zum Grunde legt, ist das, worauf die Möglichkeit äußerer Erscheinungen beruht; diese also können niemals etwas anderes enthalten, als was die Geometrie ihnen vorschreibt.	In Abschnitt (i) skizziert Kant seine Sicht: Die Geometrie bildet den Rahmen der Wahrnehmungen. In Abschnitt (ii) zeigt er die Alternative dazu, wie sie wohl von der überragenden Zahl der Physiker heute vertreten wird. Dies ist die Sicht, die Kant verwirft.
(ii) Ganz anders würde es sein, wenn die Sinne die Objekte vorstellen müßten, wie sie an sich selbst sind. Denn da würde aus der Vorstellung vom Raume, die der Geometer a priori mit allerlei Eigenschaften desselben zum Grunde legt, noch gar nicht folgen, daß alles dieses samt dem, was daraus gefolgert wird, sich gerade so in der Natur verhalten müsse. Man würde den Raum des Geometers vor bloße Erdichtung halten, und ihm keine objektive Gültigkeit zutrauen; weil man gar nicht einsieht, wie Dinge notwendig mit dem Bilde, das wir uns von selbst und zum voraus von ihnen machen, übereinstimmen müßten.	Die meisten Physiker, würden wohl zunächst einmal feststellen, dass es nicht eine, sondern unendlich viele Geometrien gibt. Es gibt unendlich viele Möglichkeiten, wie ich mit einem Axiomensystem eine Geometrie widerspruchsfrei aufbauen kann. Sie würden der Sicht aus Abschnitt (ii) durchaus zustimmen. Aus den Gesetzen der Geometrie folgt niemals zwingend, wie weitere Experimente ausgehen können. Und schon gar nicht a priori. Wie sich die Natur verhält, ob sich die Sätze einer bestimmten Geometrie in der Realität anwenden lassen, wissen wir nur aus der Beobachtung. Viele Philosophen belächeln die Physiker deswegen und bezeichnen diese Sichtweise nicht selten als ‚naiv‘. Schauen wir also genau hin, mit welchen Argumenten Kant diese Sicht verwirft! In Abschnitt (ii) stellt er fest: Die Physiker glauben, dass wir niemals mit Sicherheit wissen können, ob eine bestimmte Geometrie gilt. – Ja, das ist ja genau die Aussage der meisten Physiker.
(iii) Wenn aber dieses Bild, oder vielmehr diese formale Anschauung, die wesentliche Eigenschaft unserer Sinnlichkeit ist, vermittelst deren uns allein Gegenstände gegeben werden, diese Sinnlichkeit aber nicht Dinge an sich selbst, sondern nur ihre Erscheinungen vorstellt, so ist ganz leicht zu begreifen, und zugleich unwidersprechlich bewiesen: daß alle äußere Gegenstände unsrer Sinnenwelt notwendig mit den Sätzen der Geometrie nach aller Pünktlichkeit übereinstimmen müssen, weil die Sinnlichkeit durch ihre Form äußerer Anschauung, (den Raum) womit sich der Geometer beschäftigt, jene Gegenstände, als bloße Erscheinungen selbst allererst möglich macht.	In Abschnitt (iii) erklärt er umgekehrt, dass nach seiner Sicht jeder Geometer mit völliger Sicherheit wissen würde, dass sich die Geometrie bei allen Messungen bewähren wird. Ja, genau das ist Kants Sicht.
(iv) Es wird allemal ein bemerkungswürdiges Phänomen in der Geschichte der Philosophie bleiben, daß es eine Zeit gegeben hat, da selbst Mathematiker, die zugleich Philosophen waren, zwar nicht an der Richtigkeit ihrer geometrischen Sätze, sofern sie bloß den Raum beträfen, aber an der objektiven Gültigkeit und Anwendung dieses Begriffs selbst und aller geometrischen Bestimmungen desselben auf Natur zu zweifeln anfingen, da sie besorgten, eine Linie in der Natur möchte doch wohl aus physischen Punkten, mithin der wahre Raum im Objekte aus einfachen Teilen bestehen, obgleich der Raum, den der Geometer in Gedanken hat, daraus keinesweges bestehen kann.	Abschnitt (iv) enthält ein Beispiel, bei dem sich die Sichtweisen konkret unterscheiden. Die Physiker würden sagen: „Wir wissen a priori nicht, ob der Raum gequantelt ist, ob sich eine Strecke in unendlich kleine Stücke zerlegt werden kann oder ob es eine minimale Länge gibt, die nicht unterschritten werden kann. Ob der Raum gequantelt ist, muss das Experiment zeigen. Es sind heute Experimente im Gang, die dies untersuchen.“
(v) Sie erkannten nicht, daß dieser Raum in Gedanken den physischen d. i. die Ausdehnung der Materie selbst möglich mache: daß dieser gar keine Beschaffenheit der Dinge an sich selbst, sondern nur eine Form unserer sinnlichen Vorstellungskraft sei: daß alle Gegenstände im Raume bloße Erscheinungen, d. i. nicht Dinge an sich selbst, sondern Vorstellungen unsrer sinnlichen Anschauung sein, und, da der Raum, wie ihn sich der Geometer denkt, ganz genau die Form der sinnlichen Anschauung ist, die wir a priori in uns finden, und die den Grund der Möglichkeit aller äußern Erscheinungen (ihrer Form nach) enthält, diese notwendig und auf das präziseste mit den Sätzen des Geometers, die er aus keinem erdichteten Begriff, sondern aus der subjektiven Grundlage aller äußern Erscheinungen, nämlich der Sinnlichkeit selbst zieht, zusammen stimmen müssen. Auf solche und keine andre Art kann der Geometer wider alle Schikanen einer seichten Metaphysik, wegen der ungezweifelten objektiven Realität seiner Sätze gesichert werden, so befremdend sie auch dieser, weil sie nicht bis zu den Quellen ihrer Begriffe zurückgeht, scheinen müssen.“	Kant würde wohl im Sinne von Abschnitt (v) entgegnen: „Der Raum, den ihr Physiker ausmessen wollt, ist nur eine Form unserer sinnlichen Vorstellungskraft. Eure Uhren und Massstäbe sind blosse Erscheinungen, also nicht Dinge an sich, sondern Vorstellungen unsrer sinnlichen Anschauung. Die Gesetze der Geometrie kennen wir a priori, weil der Raum die Form der sinnlichen Anschauungen ist, die wir a priori in uns finden. Ein Messresultat kann uns nur über Sinnesreize gegeben werden und die Sinnesreize werden nach den Gesetzen der Geometrie geordnet, bevor wir sie wahrnehmen. Die Messungen können deshalb kein Resultat bringen, das nicht mit der (euklidschen) Geometrie übereinstimmt.“

Kant stellt sicher zu recht fest, dass wir nicht die Dinge an sich wahrnehmen, sondern nur Erscheinungen. Dies ändert aber überhaupt nichts an Humes Problem, wie wir Erkenntnisse gewinnen können. Wenn jemand naiv glaubt, er vermesse den Raum an sich, hat er wohl eine Vorstellung, was bei der Messung herauskommen wird. Aber er weiss es nicht sicher. Wenn wir in Kantscher Weise klar stellen, dass wir lediglich in unserer Vorstellung die Abstände der Erscheinungen in unserer Vorstellung ausmessen, haben wir wohl auch eine Vorstellung, was bei der Messung herauskommen wird. Aber woher sollen wir wissen, was bei dieser Messung in unserer Vorstellung herauskommt?

Nur weil die Messung in unserer Vorstellung stattfindet und nicht in der Welt an sich, heisst dies nicht, dass wir wissen, was dabei heraus kommt. Können wir denn vorhersagen, wie ein Traum ausgeht? – Der Traum entsteht ebenso in mir drin, wie die Erscheinungen, die ich bei einer Messung empfinde. Die Gesetze des Traumes stecken vollständig in mir. Aber trotzdem weiss ich nicht, was als nächstes passieren wird.

Kant behauptet, er wisse a priori, welche Geometrie das Raster für alle seine Sinneswahrnehmungen vorgibt. Dieses Raster lasse a priori gar keine Empfindungen zu, die der besagten Geometrie widersprechen. – Ich kann nicht für Kant urteilen. Aber ich selber habe kein solches a priori Wissen. Wenn ich es hätte, würde ich daran zweifeln, ob es nicht ein unbegründetes Vorurteil sei. Ich weiss a priori nicht, welche Geometrie gelten muss.

Kant hat nicht bewiesen, dass wir a priori wissen, welche Geometrie gilt. Er hat es nur behauptet. Sein einziges Argument ist: Wenn wir dies nicht wüssten, dann hätten wir keine Sicherheit darüber, welche Geometrie gilt. Kant setzt voraus, dass wir die Gesetze der Geometrie mit Sicherheit kennen! Da wir sicheres Wissen nicht aus Erfahrung haben können, schliesst er daraus, dass wir die Gesetze der Geometrie a priori kennen.

3.2.3. Sollen Mathematiker, die zwar von der Richtigkeit ihrer geometrischen Sätze überzeugt sind, dennoch an der objektiven Gültigkeit und Anwendung dieser geometrischen Sätze auf Natur zweifeln?

Man bemerke, dass es sich bei dieser Frage um den zentralen Streitpunkt bei der Entdeckung von Einsteins Relativitätstheorie handelt. Physiker messen heute die Natur sorgfältig aus, um herauszufinden, wie die Gesetze der Geometrie in unserem Universum sind.

Wenn die Physiker nicht an den Gesetzen der Geometrie zweifeln, wie kommen sie dann dazu, die Natur auszumessen, um genau diese Gesetze zu testen?

Die Mathematiker hatten schon vor Kants Zeit entdeckt, dass verschiedene Geometrien möglich sind. Über 2000 Jahre hatte man die Axiome der euklidschen Geometrie für unverrückbar wahr gehalten. Nun hatten Gauss und andere festgestellt, dass auch andere Axiome zu widerspruchsfreien Geometrien führen. Sie stellten sich daher die Frage, woher wir wissen, welche Geometrie die Natur am besten beschreibt. Von Gauss wissen wir, dass er die Winkel eines Dreiecks zwischen drei Bergspitzen ausmass. Manche Mathematiker und Physiker vermuten, er wollte damit testen, ob die Euklidsche Geometrie in unserer Welt gilt oder ob unsere Welt gekrümmt sei. Gauss tat also möglicherweise genau das, was Kant kritisierte!

Kant sprach immer nur von der Geometrie und meinte damit die Euklidsche Geometrie. In den Abschnitten (iv) und (v) im obigen Zitat belächelt Kant Mathematiker, die sich darüber Gedanken machen, ob die Sätze der Geometrie sich bei der Vermessung der Natur bewähren. Er hätte es absurd gefunden, die Natur auszumessen um herauszufinden, ob die Euklidsche Geometrie hier anwendbar sei. Nach Kant müssen die äusseren Erscheinungen notwendig und auf das präziseste mit den Sätzen dieser Geometrie zusammen stimmen, da diese Geometrie genau die Form der sinnlichen Anschauung ist, die wir a priori in uns finden (Abschnitt (v) im obigen Zitat). Nach dieser Geometrie werden unsere Sinnesreize geordnet, wir werden daher niemals Sinnesreize wahrnehmen, die dieser Geometrie widersprechen.

Folgen wir aber Kants Erklärung und fragen wir uns: Woher glaubt Kant zu wissen, dass alle Sinneswahrnehmungen der Euklidschen Geometrie folgen?

Kant beweist oder begründet diese Behauptung nirgends! – Daran ändert auch sein Vorbehalt nichts, dass sich die Gesetze der Geometrie nur auf die Erscheinungen beziehen und nicht auf Dinge an sich. Zwar gehen wohl die meisten Physiker davon aus, dass die Erscheinungen, die sie wahrnehmen in den Dingen an sich ein Äquivalent haben. Aber man kann problemlos auch sagen, wenn Physiker den Raum vermessen, vermessen sie den inneren Raum, in den die Erscheinungen geordnet werden. Nach Kant dürften sie hier nichts anderes finden, als die Euklidsche Geometrie. Denn nach Kant ist etwas anderes gar nicht denkbar.

Nichteuklidsche (gekrümmte) Geometrien sind aber sehr wohl denkbar! Es ist auch nicht so, dass der Euklidsche Raum allen anderen Geometrien so weit überlegen ist, dass in der Praxis gar nichts anderes denkbar ist. Friedrich Gauss z. B. war von seiner Entdeckung der gekrümmten Geometrien tief beeindruckt und war überzeugt, erst dadurch wirklich verstanden zu haben, was ein Raum überhaupt ist. Gekrümmte Geometrie ist zwar ungewohnt, aber wir können sie uns durchaus vorstellen. Wer nicht gerne abstrakt denkt, kann sich heute einfach Filme anschauen, in denen gekrümmte Geometrien gezeigt werden. Z. B. bei diesem externen Link: Didaktisches Material und Animationen zur Relativitätstheorie (Siehe insbesondere die Animation zum Wurmloch. Hier kriegt man ein Gefühl dafür, wie es ist, im gekrümmten Raum zu leben.)

Wenn wir in einer Welt leben würden, wie der obige Film sie zeigt, würden wir uns sehr rasch daran gewöhnen, dass der Raum nicht euklidisch ist. Wir würden dank unseren Erfahrungen eine andere Geometrie für selbstverständlich halten.

Nach den bisherigen Argumenten ist also keineswegs klar, ob es synthetische Urteile a priori gibt. Humes Zweifel ist keineswegs beseitigt. Und Kant hat kein einziges haltbares Argument vorgebracht, weshalb Physiker nicht den Raum vermessen sollen, um herauszufinden, welche Geometrie darin gilt. Betrachten wir nun, wie nach Kant unser Wissen in den Naturwissenschaften begründet werden soll.

3.3. Die Argumente zu den Naturwissenschaften

Die ursprüngliche Frage, nämlich Humes Entdeckung, dass das Kausalitätsgesetz durch noch so viele Erfahrungen nicht bewiesen werden kann, gehört zum zweiten Stamm der menschlichen Erkenntnis, zum Verstand. Um Naturgesetze zu finden, müssen wir die Erscheinungen in Begriffe fassen und dies geschieht durch den Verstand. Kant geht das Problem ähnlich an, wie die Fragen nach Raum und Zeit, allerdings mit einem kleinen Unterschied.

Wie bei den Gesetzen von Raum und Zeit stellte Kant auch bei der Kausalität fest, dass wir auch durch noch so viele Erfahrungen nie absolut sicher wissen können, dass das Kausalitätsgesetz immer gelten muss. Dieser Schluss hatte ja Hume zum Skeptizismus getrieben. Kant dagegen wollte den Zweifel um jeden Preis vermeiden und behauptete ganz einfach, wir wüssten a priori, dass das Kausalitätsgesetz immer gelte.

3.3.1. Die Urteilstafel und die Kategorientafel

Damit aus den Sinnesempfindungen Erkenntnis wird, muss der Verstand Urteile bilden. Urteile bestehen darin, dass einem Subjekt (z. B. ‚der Schwan‘) ein Prädikat (z. B. ‚ist weiss‘) zugeordnet wird. Welche Urteile möglich sind, entnimmt Kant der klassischen Urteilstafel. Die Urteilstafel ist in vier sogenannten Titeln organisiert. Jeder Titel umfasst einen bestimmten Formaspekt von Urteilen. Zu jedem dieser Formaspekte gibt es drei Optionen, die Kant Momente nennt. Die Form eines Urteils ist nach Kant dann vollständig charakterisiert, wenn man ihm unter jedem Titel genau ein Moment zugeordnet hat.

Beispiel: Das Urteil, dass alle Schwäne weiss sind, ist kategorisch, allgemein, assertorisch und bejahend.

Die Urteilstafel

In der folgenden Urteilstafel kommen die Beispiele in Klammern z. T. mehrmals vor. In diesen Fällen werden sie nur klar, wenn man sich auf den richtigen Formaspekt konzentriert. So taucht ”Der Schwan ist weiss“ mehrmals in der Tafel auf. Unter Qualität kommt es dabei darauf an, dass das Urteil nicht verneint ist; unter Relation ist wichtig, dass das Urteil nicht hypothetisch oder disjunktiv ist.

1. Quantität allgemein (Alle Schwäne sind weiss) besonders (Ein Schwan ist weiss) einzeln (Genau ein Schwan ist weiss)	2. Qualität bejahend (Der Schwan ist weiss) verneinend (Der Schwan nicht ist weiss) unendlich (Der Schwan ist nicht nichtweiss)
3. Relation kategorisch (Der Schwan ist weiss) hypothetisch (Wenn der Schwan weiss ist, dann ist der Schwan hell) disjunktiv (Der Schwan ist weiss oder der Schwan ist schwarz oder…)	4. Modalität problematisch (Der Schwan ist möglicherweise weiss) assertorisch (Der Schwan ist weiss) apodiktisch (Der Schwan ist notwendig weiss)

 

Zu jedem Moment der Urteilstafel gehört nun eine Kategorie in der Kategorientafel. Wenn ich alle Schwäne zusammenfasse, bilde ich eine Einheit. Zum Moment allgemein in der Urteilstafel gehört also z. B. die Kategorie Einheit. Also steht in der Kategorientafel an erster Stelle unter Quantität die Einheit. Auf diese Weise wird jedes Moment zu einen Begriff zusammengefasst, was die Kategorientafel ergibt.

Die Kategorientafel

1. Kategorien der Quantität Einheit Vielheit Allheit	2. der Qualität Realität Negation Limitation
3. der Relation der Inhärenz und Subsistenz der Kausalität und Dependenz der Gemeinschaft	4. der Modalität Möglichkeit / Unmöglichkeit Dasein / Nichtsein Notwendigkeit / Zufälligkeit

Es ist umstritten, wie stringent oder wie willkürlich der Schritt zur Kategorientafel ist. Schoppenhauer z. B. meinte, die einzige wahre Kategorie sei die Kausalität, auf der auch fast alle von Kants Beispielen beruhen. Diese Frage muss uns hier aber nicht weiter kümmern. Es geht ja hier um die Frage, ob man nach Kants Vorbild zu einer brauchbaren Erkenntnistheorie kommen kann. Wenn Kant es selber als Pionier nicht geschafft hat, wäre das ein entschuldbarer Fehler, wenn die Idee dahinter funktioniert.

3.3.2. Von den Kategorien zum Wissen a priori

Hier geht es vorerst nur darum, Kants Idee zu verstehen, unabhängig davon, ob er bei der Wahl der Kategorien eine glückliche Hand bewies. Was will Kant mit den Kategorien, bzw. mit den so gewonnenen Begriffen? – Kant KrdrV § 14: “Nun enthält aber alle Erfahrung ausser der Anschauung der Sinne, wodurch etwas gegeben wird, noch einen Begriff von einem Gegenstande, der in der Anschauung gegeben wird oder erscheint: demnach werden Begriffe von Gegenständen überhaupt als Bedingungen a priori aller Erfahrungserkentnis zum Grunde liegen: folglich wird die objektive Gültigkeit der Kategorien als Begriffe a priori darauf beruhen, daß durch sie allein Erfahrung (der Form des Denkens nach) möglich sei. Denn alsdann beziehen sie sich notwendiger Weise und a priori auf Gegenstände der Erfahrung, weil nur vermittelst ihrer überhaupt irgend ein Gegenstand der Erfahrung gedacht werden kann.”

Die Argumentation geht hier analog zu den Sätzen der Geometrie: Die in der Kategorientafel aufgelisteten Begriffe sind die Bedingung, dass Erkenntnis überhaupt möglich ist. Nur wenn ich Gegenstände der Anschauung nach diesen Begriffen verknüpfen kann, kann ich denken.

Es ist nicht bei allen Kategorien gleich klar, weshalb sie für unser Denken a priori notwendig sein sollen. Bei der Kausalität, die ja auch der Ausgangspunkt zu seinen Überlegungen war, begründet Kant dies am ausführlichsten. Kant muss hier zeigen: Damit wir überhaupt Denken können, das heisst, damit wir verschiedene Vorstellungen miteinander verknüpfen können, müssen wir a priori das Wissen um die Kausalität haben. Kants Argumentation dazu:

“Zu aller Erfahrung und deren Möglichkeit gehört Verstand, … [der]die Zeitordnung auf die Erscheinungen überträgt. … Diese Bestimmung der Stelle kann nun nicht von dem Verhältnis der Erscheinungen gegen die absolute Zeit entlehnt werden, (denn die ist kein Gegenstand der Wahrnehmung,) sondern umgekehrt, die Erscheinungen müssen einander ihre Stellen in der Zeit selbst bestimmen, und dieselbe in der Zeitordnung notwendig machen, d. i. dasjenige, was da folgt, oder geschieht, muss nach einer allgemeinen Regel auf das, was im vorigen Zustande enthalten war, folgen,…
Der Grundsatz des Kausalitätsverhältnisses in der Folge der Erscheinungen gilt daher auch vor allen Gegenständen der Erfahrung (unter der Bedingung der Sukzession), weil er selbst der Grund der Möglichkeit einer solchen Erfahrung ist.” (KrdrV B Zweite Analogie, `Grundsatz der Zeitenfolge nach dem Gesetz der Kausalität)

Wenn die Zeit nicht den Dingen an sich anhaftet, sondern ausschliesslich ein Ordnungsschema ist, nach dem wir unsere Wahrnehmungen ordnen, dann fehlt den Erscheinungen das Kriterium, nach dem sie geordnet werden sollen. Was vorher und was nachher kommt, ist in den Dingen an sich ja – nach Kant – nicht gegeben, also muss es bei der Wahrnehmungen den Erscheinungen hinzugefügt werden. Dies leistet nach Kant der Verstand, der nach dem Kausalitätsgesetz die Ordnung einführt.

Zunächst bringt sich Kant in die Bredouille, indem er behauptet, die Zeit gehöre nicht zur Welt an sich. Weil er aber die offensichtliche Ordnung in den Erscheinungen nicht verleugnen kann, verschiebt er auch das Kausalitätsgesetz von der Welt an sich zu den Erscheinungen. Diese Ordnung, die wir wahrnehmen, soll nun nichts mit der Welt an sich zu tun haben? Wie kann es da sein, dass ich mich trotz solcher Wahnvorstellungen in der Welt recht gut zurecht finde und diese Welt auch nicht als feindlich erlebe? – Ein Wahnsinniger mag zwar jede Konfrontation mit der Realität in seinen Wahn einordnen können. Er wird seine Umwelt aber als sehr feindselig erleben, weil sie sich immer wieder entgegen seiner Einbildung verhält. Oder, anders gefragt: Wenn meine Wahrnehmung mit der Welt an sich nichts zu tun hat, was könnte es für eine Rolle spielen, wenn ich mir eine das Bild verzerrende Brille aufsetze?

3.3.3. Das Induktionsproblem

Alle Urteile der Naturwissenschaften können nach Kant also einer der obigen Kategorie zugeordnet werden. Kants Schlüsselidee ist nun: Unsere Erkenntnisse können nur in diesem von den Kategorien gesteckten Rahmen liegen, so wie unsere Sinneswahrnehmungen durch den Rahmen beschränkt sind, der durch die Gesetze von Raum und Zeit gesteckt sind. Dass dieser Schluss gewagt ist, ist Kant durchaus bewusst.

Im Fall der Kausalität handelt sich hier wieder um das Humesche Induktionsproblem. Kant erklärt das Problem im folgenden hier noch einmal und schliesst mit einem Satz, der deswegen bemerkenswert ist, weil er das einzige Argument ist, das er gegen Humes skeptische Position vorzubringen hat:

„Gedächte man sich von der Mühsamkeit dieser Untersuchungen dadurch loszuwickeln, daß man sagte: Die Erfahrung böte unablässig Beispiele einer solchen Regelmäßigkeit der Erscheinungen dar, die genugsam Anlaß geben, den Begriff der Ursache davon abzusondern, und dadurch zugleich die objektive Gültigkeit eines solchen Begriffs zu bewähren, so bemerkt man nicht, daß auf diese Weise der Begriff der Ursache gar nicht entspringen kann, sondern daß er entweder völlig a priori im Verstande müsse gegründet sein, oder als ein bloßes Hirngespinst gänzlich aufgegeben werden müsse. Denn dieser Begriff erfordert durchaus, daß etwas A von der Art sei, daß ein anderes B daraus notwendig und nach einer schlechthin allgemeinen Regel folge. Erscheinungen geben gar wohl Fälle an die Hand, aus denen eine Regel möglich ist, nach der etwas gewöhnlichermaßen geschieht, aber niemals, daß der Erfolg notwendig sei: daher der Synthesis der Ursache und Wirkung auch eine Dignität anhängt, die man gar nicht empirisch ausdrücken kann, nämlich, daß die Wirkung nicht bloß zu der Ursache hinzukomme, sondern durch dieselbe gesetzt sei, und aus ihr erfolge. Die strenge Allgemeinheit der Regel ist auch gar keine Eigenschaft empirischer Regeln, die durch Induktion keine andere als komparative Allgemeinheit, d.i. ausgebreitete Brauchbarkeit bekommen können. Nun würde sich aber der Gebrauch der reinen Verstandesbegriffe gänzlich ändern, wenn man sie nur als empirische Produkte behandeln wollte.” (KrdrV, § 13)

Kant verwirft Humes Position, weil man nach dem Skeptizismus nicht mehr sagen könnte: Die Kausalität gilt immer und überall. Darüber hinaus findet man bei Kant kein Argument gegen Hume. Hume hat bewiesen, dass das Kausalitätsgesetz nicht aus der Erfahrung abgeleitet werden kann und hat daraus geschlossen, dass wir nie mit Sicherheit wissen können, ob es gilt. Im Kern lautet Kants Erkenntnistheorie: Da das Kausalitätsgesetz nicht aus der Erfahrung abgeleitet werden kann, muss es a priori gelten! Dass es nicht allgemein gelten könnte, zog er gar nicht in Erwägung.

In seinem grossen Werk weist Kant weder nach, dass Hume sich geirrt hat, noch beweist er, dass das Kausalitätsgesetz allgemein gilt. Beides versucht er schon gar nicht. Sein Werk ist ein heroischer Versuch nachzuweisen, dass kein Widerspruch entstehen würde, wenn wir annehmen würden, wir wüssten a priori, dass das Kausalitätsgesetz allgemein gilt. Nur weil etwas nicht in Widersprüche führt, heisst dies aber nicht, dass wir es mit absoluter Sicherheit wissen. Humes skeptische Position ist dadurch also in keiner Weise widerlegt oder auch nur erschüttert.

3.3.4. Die Kategorien schreiben der Natur die Gesetze vor

Kant lässt keinen Zweifel am Kausalitätsgesetz zu. Wie aber kann es sein, dass wir vom Kausalitätsgesetz mit absoluter Sicherheit wissen, wenn diese Sicherheit nicht aus der Erfahrung stammen kann?

Kant dazu Kritik der reinen Vernunft § 27:
„Nun sind nur zwei Wege, auf welchen eine n o t w e n d i g e Übereinstimmung der Erfahrung mit den Begriffen von ihren Gegenständen gedacht werden kann: entweder die Erfahrung macht diese Begriffe, oder diese Begriffe machen die Erfahrung möglich“

Die Hervorhebung von n o t w e n d i g e stammt von Kant. Auch dieser Satz zeigt, dass Kant das Kausalitätsgesetz gar nie hinterfragt. Er behauptet ganz einfach, dass wir hierüber ja absolute Sicherheit hätten und fragt sich, wie das sein kann.

Da die Erfahrung nicht zu dieser (postulierten) absoluten Sicherheit über das Kausalitätsgesetz führen kann, bleibt nur der zweite Weg. Wie können die Begriffe die Erfahrung möglich machen? – Kant dazu (Kritik der reinen Vernunft § 26):
„Kategorien sind Begriffe, welche den Erscheinungen, mithin der Natur, als dem Inbegriffe aller Erscheinungen (natura materialiter spectata), Gesetze a priori vorschreiben, und nun frägt sich, da sie nicht von der Natur abgeleitet werden und sich nach ihr als ihrem Muster richten (weil sie sonst bloss empirisch sein würden), wie es zu begreifen sei, dass die Natur sich nach ihnen richten müsse, d. i. wie sie die Verbindung des Mannigfaltigen der Natur, ohne sie von dieser abzunehmen, a priori bestimmen können. Hier die Auflösung dieses Rätsels.

Es ist um nichts befremdlicher, wie die Gesetze der Erscheinungen in der Natur mit dem Verstande und seiner Form a priori, d. i. seinem Vermögen das Mannigfaltige überhaupt zu v e r b i n d e n d e n , als wie die Erscheinungen selbst mit der Form der sinnlichen Anschauung a priori übereinstimmen müssen. Denn Gesetze existieren eben so wenig in den Erscheinungen sondern nur relativ zum Subjekt,…
…
Erscheinungen sind nur Vorstellungen von Dingen, die, nach dem, was sie an sich sein mögen, unerkannt sind. Als blosse Vorstellungen aber stehen sie unter gar keinem Gesetze der Verknüpfung, als demjenigen, welches das verknüpfende Vermögen vorschreibt.
…
Da nun … alle mögliche Wahrnehmung … von den Kategorien abhängt, so müssen alle mögliche Wahrnehmungen, mithin auch alles, was zum empirischen Bewusstsein immer gelangen kann, d. i. alle Erscheinungen der Natur, ihrer Verbindung nach unter den Kategorien stehen, von welchen die Natur (bloss als Natur überhaupt betrachtet), als dem ursprünglichen Grunde ihrer notwendigen Gesetzmässigkeit (als natura formaliter spectata), abhängt.“

Wie bei den Gesetzen von Raum und Zeit läuft Kants Argument also auch hier darauf hinaus, dass wir über die Welt an sich zwar nichts aussagen können, dass wir aber die Gesetzmässigkeiten der Wahrnehmungen, die wir von dieser Welt haben, a priori kennen. Wie oben müssen wir uns aber auch fragen, ob wir wirklich a priori diese Gesetzmässigkeiten kennen. Bei den Gesetzen des Raumes nahm Kant die euklidsche Geometrie als Basis und verleugnete, dass auch andere Geometrien denkbar wären. Er behauptete ganz einfach, wir wüssten a priori, dass die Gesetze der euklidschen Geometrie gelten müssen.

Hier unterliegt er noch einmal dem gleichen Denkfehler. Statt auf die euklidsche Geometrie stützt er sich hier auf die Kategorientafel. Allein schon die Tatsache, dass andere Philosophen andere Tafeln benützen (Schoppenhauer z. B. fand, die einzige wahre Kategorie sei die Kausalität), zeigt, dass diese Tafel keine absolute Sicherheit ausstrahlt. Kant müsste nachweisen, dass wir beim Bilden von Urteilen zwingend die Kategorientafel brauchen und dass diese genau die notwendig gültigen Gesetze unserer Wahrnehmung enthalten. Selbst dann ist der Schluss aber nicht a priori. Denn es handelt sich einfach um das anthropische Prinzip, das auf der Beobachtung beruht, dass wir bewusst denkende Lebewesen sind. Das anthropische Prinzip führt nicht zu Urteilen a priori.

Eine Begründung, weshalb Kant mit seiner Idee des a priori scheitern muss, findet man in Abschnitt 5.

4. Eine Reihe von Irrtümern, denen Kant mit seiner Erkenntnistheorie eine Grundlage schafft

4.1. Vorbemerkung zu den Irrtümern

Es ist bezeichnend, dass Kant sich praktisch immer irrte, wenn er ein Beispiel für ein synthetisches Urteil a priori anführte. Anhänger Kants werden dem entgegnen, Kant könne gar nicht geirrt haben. Wenn Urteile a priori, also unabhängig von der Erfahrung, gelten, können sie durch Erfahrung nicht widerlegt werden.

Bei dieser ‚Beweisführung‘ wird aber das vorausgesetzt, was bewiesen werden sollte! – Die Frage ist ja, ob die von Kant genannten Beispiele Urteile a priori sind. Kant behauptete dies und hätte dies beweisen müssen.

Viele Philosophen halten die folgenden Kantzitate für verzeihliche und unbedeutende Irrtümer, die Kants Leistung nicht schmälern. Zu Kants Zeit waren die Naturwissenschaften eben noch nicht so weit. Jeder Mensch irrt sich ab und zu, weshalb sollen wir Kant einzelne Irrtümer übel nehmen?

Der Punkt ist, dass Kant seine ganze Theorie auf der Behauptung aufbaut, dass er sich in den Urteilen a priori gar nicht irren kann! Schon wenn sich ein einziges Urteil a priori als falsch herausstellt, muss dies zutiefst beunruhigend sein. Denn jeder Fehler beweist, dass wir nicht in der Lage sind, a priori unerschütterlich wahre Urteile zu fällen, dass also Kants Grundannahme falsch ist. Wenn auch nur ein Urteil, das wir ursprünglich für sicher gehalten haben, sich plötzlich als unsicher herausstellt, bricht das ganze kunstvolle Gebäude zusammen und es bleibt nichts als der Zweifel.

Ich habe die Irrtümer in drei Kategorien eingeteilt, was die folgenden drei Abschnitte ergibt.

4.2. Behauptungen, die sich durch fragwürdige Definitionen retten lassen

Kritik der reinen Vernunft – Einleitung: IV Von dem Unterschiede analytischer und synthetischer Urteile
…
„Z. B. wenn ich sage: alle Körper sind ausgedehnt, so ist dies ein analytisch Urteil. Denn ich darf nicht über den Begriff, den ich mit dem Körper verbinde, hinausgehen, …
Denn es wäre ungereimt, ein analytisches Urteil auf Erfahrung zu gründen, weil ich aus meinem Begriffe gar nicht hinausgehen darf, um das Urteil abzufassen, und also kein Zeugnis der Erfahrung dazu nötig habe.“

Natürlich kann man den Begriff ‚Körper‘ definieren, als etwas, das eine Ausdehnung hat. Es fragt sich, ob eine solche Definition nützlich ist. Wenn sich nun herausstellt, dass ein Elektron keine Ausdehnung hat, sind Elektronen keine Körper mehr. Vielleicht würden wir dann bei der Betrachtung der Welt plötzlich feststellen, dass es gar keine Körper gibt oder dass gewisse Dinge am Montag, Dienstag und Mittwoch Körper sind, aber an den anderen Wochentagen nicht.

Gerade das Beispiel Elektron zeigt auch, dass die Frage ob es ausgedehnt oder punktförmig ist, nicht so leicht zu beantworten ist. Es kann nämlich auch beides sein, je nachdem wie die Begriffe ‘ausgedehnt’ und ‘punktförmig’ definiert werden.

Die Frage ist, wie sinnvoll es ist, die Begriffe so starr zu definieren und keine Korrektur zu erlauben, auch wenn die Experimente danach schreien. Begriffe werden aufgebaut beim Begreifen, also im direkten Kontakt mit der Natur. Wenn wir nach Kant verfahren würden, müssten wir nach jeder neuen Erkenntnis, neue Begriffe erfinden. Die Atome wären dann plötzlich keine Atome mehr, nur weil sie jemand gespalten hat.

4.3. Behauptungen, die durch die moderne Physik widerlegt sind

„Einleitung S. 67: Naturwissenschaft (Physica) enthält synthetische Urteile a priori als Prinzipien in sich. Ich will nur ein paar Sätze zum Beispiel anführen, als den Satz: dass in allen Veränderungen der körperlichen Welt die Quantität der Materie unverändert bleibe, …“

Nach der Formel E=mc² kann Materie in Energie umgewandelt werden. Die Quantität der Materie ist also nicht unverändert.

„S. 86 (Nur in der ersten Fassung der KdrV: Auf diese Notwendigkeit a priori gründet sich die apodiktische Gewissheit aller geometrischen Grundsätze, und die Möglichkeit ihrer Konstruktionen a priori. Wäre nämlich diese Vorstellung des Raums ein a posteriore erworbener Begriff, der aus der allgemeinen äusseren Erfahrung geschöpft wäre, so würden die ersten Grundsätze der mathematischen Bestimmung nichts als Wahrnehmungen sein. Sie hätten also alle Zufälligkeit der Wahrnehmungen, und es wäre eben nicht notwendig, dass zwischen zwei Punkten nur eine gerade Linie sei, sondern die Erfahrung würde es so jederzeit lehren. Was von der Erfahrung entlehnt ist, hat auch nur komparative Allgemeinheit, nämlich durch Induktion. Man würde also nur sagen können, so viel zur Zeit noch bemerkt worden, ist kein Raum gefunden worden, der mehr als drei Abmessungen hätte.“

Es ist nicht notwendig, dass es zwischen zwei Punkten überhaupt eine gerade Linie gibt. Im gekrümmten Raum der allgemeinen Relativitätstheorie gibt es normalerweise keine gerade Linie zwischen zwei Punkten, denn Geodäten sind im allgemeinen krumm. Wenn wir grosszügigerweise eine Geodäte gerade nennen wollen, gäbe es mehrere Geraden zwischen zwei Punkten, was Kant sicher auch nicht erwartet hätte.

Wie viele Dimensionen der Raum hat, ist auch nicht a priori bestimmt. Aus der Erfahrung wissen wir, dass es in unserer Umgebung nur drei sichtbare Raum-Dimensionen gibt. In der Stringtheorie geht man aber z. B. von 11 Dimensionen aus, wovon 8 nur deshalb nicht sichtbar sind, weil sie zusammen gerollt sind. Anders als Kant behauptete, sind wir tatsächlich in der Situation, dass wir die Natur anschauen müssen, um zu wissen, welche Geometrie hier gilt.

Prolegomena Erster Teil, Wie ist reine Mathematik möglich? §10:

„Beide Vorstellungen [Raum und Zeit] aber sind bloß Anschauungen, denn wenn man von den empirischen Anschauungen der Körper und ihrer Veränderungen (Bewegung) alles Empirische, nämlich was zur Empfindung gehört, wegläßt, so bleiben noch Raum und Zeit übrig, welche also reine Anschauungen sind, die jenen a priori zum Grunde liegen, und daher selbst niemals weggelassen werden können…“

Als Einstein bei seiner Ankunft in New York 1921 nach einer kurzen Erklärung seiner Relativitätstheorie gefragt wird, antwortet er: „Früher hat man geglaubt, wenn alle Dinge aus der Welt verschwinden, so bleiben noch Raum und Zeit übrig. Nach der Relativitätstheorie verschwinden aber Zeit und Raum mit den Dingen.“

Auch abgesehen von der Relativitätstheorie scheint mir, zumindest den Raum könnte man problemlos auch weg lassen. Denn wenn ich im Halbschlaf Musik höre oder einen Duft rieche, nehme ich über meine Sinne durchaus etwas wahr, ohne dazu einen Raum als Form zu benötigen. Mir scheint auch, Gefühle im Halbschlaf können durchaus zeitlos sein.

4.4. Urteile a priori, die zwar noch nicht widerlegt sind, aber nicht zwingend erscheinen

Es sind keineswegs alle von Kants Beispielen bereits widerlegt. Kants Erkenntnistheorie gerät aber schon ins Wanken, wenn Sätze, die er als unerschütterlich wahr bezeichnete, plötzlich nicht mehr so sicher erscheinen. Kants Erkenntnistheorie erträgt keine Unsicherheit, im Unterschied zu Theorien der Naturwissenschaften. Wenn die Steine nicht ganz so hinunter fallen, wie Newton es beschrieb, müssen wir das Gravitationsgesetz eben anpassen. Dies bedeutet aber nicht, dass die ganze Physik zusammenbricht. Anders als Kant nennt aber kein Physiker seine Behauptungen unerschütterlich wahr.

Kants Theorie funktioniert nur, wenn absolute Sicherheit überhaupt möglich ist. Wir müssen uns ständig fragen: Ist diese Sicherheit nur eingebildet oder können wir uns tatsächlich darauf verlassen? – Wenn plötzlich ein Satz zweifelhaft wird, der nach Theorie unerschütterlich wahr ist, beweist dies, dass die Sicherheit nur eingebildet sein kann. Dann bleibt aber nichts als der Humesche Zweifel.

Deshalb sind auch die folgenden Sätze ernsthafte Probleme für Kants Erkenntnistheorie.

KrdrV, Einleitung V, S. 68:„… z. B. in dem Satze: die Welt muss einen ersten Anfang haben, u. a. m. und so besteht Metaphysik wenigstens ihrem Zwecke nach aus lauter synthetischen Sätzen a priori.“

Kant hielt es also für unbezweifelbar sicher, dass die Welt einen ersten Anfang hat. Etwas anderes ist für ihn gar nicht denkbar, also muss es so sein. Physiker erwägen heute aber durchaus auch andere Modelle, z. B. ein pulsierendes Universum. Was sollen wir davon halten, wenn ein Erkenntnistheoretiker behauptet, solche Modelle seien grundsätzlich undenkbar? – Physiker denken solche Modelle!

KrdrV, Einleitung V, S. 67: „Naturwissenschaft (Physica) enthält synthetische Urteile a priori als Prinzipien in sich. Ich will nur ein paar Sätze zum Beispiel anführen, als den Satz: … dass, in aller Mitteilung der Bewegung, Wirkung und Gegenwirkung jederzeit einander gleich sein müssen.“

Ob Wirkung immer gleich Gegenwirkung sein muss, weiss ich nicht. Ich kenne zwar keine Ausnahme, aber ganz sicher bin ich mir nicht. Zumindest wissen die Menschen dies nicht a priori. Es brauchte Genies wie Galilei und Newton, die auf diesen Satz hinwiesen. Aristoteles z. B. hatte noch eine ganz andere Vorstellung von den Wechselwirkungen. Wenn der Satz von Wirkung und Gegenwirkung a priori jedem Menschen gegeben ist, wie kommt es dann, dass Aristoteles eine so andere Vorstellung von diesem Satz hat?

KrdrV, S. 86: „… Denn erstlich kann man sich nur einen einigen Raum vorstellen, und wenn man von vielen Räumen redet, so verstehet man darunter nur Teile eines und desselben alleinigen Raumes.“

Mathematiker und Physiker können sich durchaus Räume vorstellen, die nicht zusammen hängen und die Löcher aufweisen (Multiversen, Blasenuniversum, Parallelwelten, …).

KrdrV, S. 86: „… Er (der Raum) ist wesentlich einig, das Mannigfaltige in ihm, mithin auch der allgemeine Begriff von Räumen überhaupt beruht lediglich auf Einschränkungen. Hieraus folgt, dass in Ansehung seiner eine Anschauung a priori (die nicht empirisch ist) allen Begriffen von demselben zum Grunde liegt. So werden auch alle geometrische Grundsätze, z. B. dass in einem Triangel zwei Seiten zusammen grösser seien, als die dritte niemals aus allgemeinen Begriffen von Linie und Triangel, sondern aus der Anschauung und zwar a priori mit apodiktischer Gewissheit abgeleitet.“

Der Satz, dass in einem Triangel zwei Seiten zusammen grösser seien, als die dritte, ist keineswegs notwendig. Es gibt durchaus Geometrien, in denen dieser Satz nicht allgemein gilt. Wenn es Wurmlöcher gibt, gilt der Satz sicher nicht.

KrdrV, S. 86: „Der Raum wird als eine unendliche gegebene Grösse vorgestellt.“

Es ist durchaus möglich, sich endliche Räume vorzustellen. Es ist eine wichtige Frage der Kosmologie, ob das Universum unendlich oder endlich ist. Physiker werden diese Frage durch Messungen beantworten. Es handelt sich hier also nicht um ein a priori Wissen.

KrdrV, S. 88 „Geometrie ist eine Wissenschaft, welche die Eigenschaften des Raums synthetisch und doch a priori bestimmt. … Denn die geometrischen Sätze sind insgesamt apodiktisch, d. i. mit dem Bewusstsein ihrer Notwendigkeit verbunden, z. B. der Raum hat nur drei Abmessungen; dergleichen Sätze aber können nicht empirische oder Erfahrungsurteile sein, noch aus ihnen geschlossen werden.“

Es ist a priori überhaupt nicht klar, wie viele Dimensionen der Raum hat.

Kant behauptet also, kein Experiment der Welt könne nachweisen, dass die Welt mehr als drei Dimensionen habe. Es gibt aber durchaus experimentell überprüfbare Theorien, nach denen die Welt mehr als drei Dimensionen hat. In der Quantentheorie rechnet man in einem unendlichdimensionalen Hilbertraum. Kaluzza und Klein haben die elektrische Kraft in einer fünfdimensionalen Raumzeit beschrieben. Die Stringtheorien basieren auf dieser Idee. Nach diesen hat der Raum mehr als drei Dimensionen, wobei allerdings alle bis auf drei so eng zusammen gerollt sind, dass wir sie nicht sehen können. Nach Andrej Lindes Theorie des Blasenuniversums ist die Anzahl der Dimensionen nicht in jeder Blase gleich. Es gibt auch eine bemerkenswerte Theorie, die besagt, das Universum sei ein Hologramm und habe nur zwei Dimensionen. Vielleicht ist das Universum ein Fraktal und hat keine ganzzahlige Dimension. All dies zeigt, dass die Physiker den Vorurteilen wesentlich weniger unterliegen als Kant es für absolut notwendig hielt.

Natürlich ist unser Raum nahezu dreidimensional. Das sehen wir. Das bedeutet aber doch nicht, dass wir schon bevor wir überhaupt hinschauen, wissen, dass der Raum exakt dreidimensional ist!

Dies wäre Kants Kernaussage: Wir müssen überhaupt nicht mehr hinschauen wie der Raum ist. Denn der muss so sein, wie wir ihn uns vorstellen. Auf solchen Glaubenssätzen basieren die Religionen, die Esoterik und der Okkultismus. Dass Kant im Vergleich zu seinen Zeitgenossen ein Aufklärer war, ändert nichts daran.

4.5. Eine andere Interpretation von Kants Apriori

Viele Kantianer sind der Ansicht, Kants Erkenntnistheorie widerspreche Einsteins Relativitätstheorie nicht. Kant schliesse nicht aus, dass es andere Geometrien gibt und dass wir z. B. die Erscheinungen mit einer gekrümmten Geometrie ebenso gut beschreiben können. Sie meinen aber, die Geometrie sei lediglich die Form, nach der wir die Erscheinungen ordnen und habe mit der realen Welt nichts zu tun. Wenn wir die Erscheinungen nach einer gekrümmten Geometrie ordnen, dann kann kein Experiment diese Ordnung widerlegen. Wenn wir sie nach der euklidschen Geometrie ordnen, dann werden wir damit ebenfalls nicht auf Widersprüche zu den Experimenten stossen. Dies gelte so für alle Urteile a priori. A priori ist das Raster festgelegt. Dieses Raster legt auch fest, was wir sehen können.

Ich halte dies für Unsinn und glaube nicht, dass Kant dies meinte. Im konkreten Fall der Dimensionalität bedeutet es nämlich folgendes: Über die Welt an sich können wir nichts aussagen. Diese bleibt uns verborgen. Wir können aber die Erscheinungen nach verschiedenen Schemen ordnen, z. B. in einen dreidimensionalen Raum. Ebensogut können wir die Erscheinungen aber auch in einen zwei- oder vierdimensionalen Raum ordnen. Diese Form, in die wir die Erscheinungen ordnen, gibt vor, wie wir die Welt erleben. Experimentell können wir nicht zwischen guten und schlechten Schemen unterscheiden.

Konkret könnte es nach dieser Interpretation Menschen geben, die die Erscheinungen zweidimensional ordnen. Diese würden z. B. Schweine sehen, die beim Essen in zwei Teile zerfallen. Andere Menschen sehen dreidimensionale Schweine, die nicht zerfallen. Verdoppelt man bei einem zweidimensionalen Schwein alle Längen, so wird es viermal so schwer. Verdoppelt man bei einem vierdimensionalen Schwein alle Längen, so wird es sechzehnmal so schwer. Trotzdem können ein zwei- ein drei- und ein vierdimensional wahrnehmender Beobachter mit keinem Experiment entscheiden, wer recht hat. Denn die Dimensionalität würde ja nur durch die Einordnung entstehen und wäre völlig unabhängig von den Dingen an sich sein. Diese Vorstellung scheint mir nicht haltbar.

Abbildung 1. Eine andere Interpretation von Kants Apriori. Ein Mensch kann die Erscheinungen ebenso gut in einen zweidimensionalen Raum ordnen, wie in einen dreidimensionalen. Der zweidimensional Wahrnehmende sieht, wie ein Schwein beim Fressen in zwei Stücke zerfällt. Der dreidimensional Wahrnehmende sieht keine Teilung. Trotzdem soll es kein Experiment geben, das zwischen den zwei Wahrnehmungen unterscheidet. Ich glaube nicht, dass Kant sein Apriori so verstand.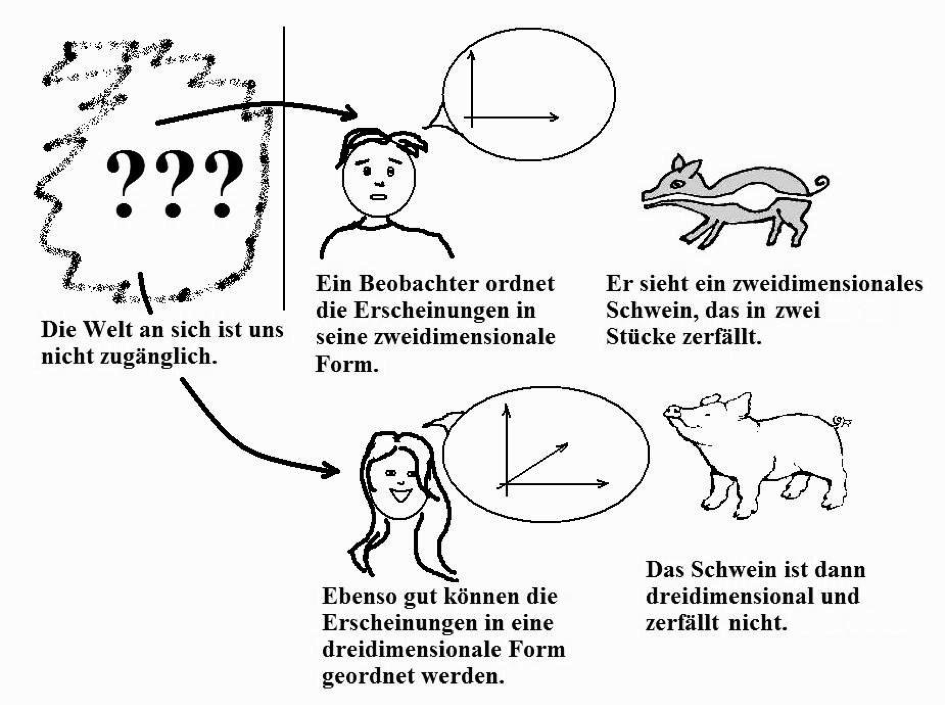

5. Einschätzung von Kants Ideen

Nach dem oben Gesagten werden einige nun behaupten, ich hätte Kant missverstanden, ich hätte die stringenten Argumente übersehen und die falschen Stellen zitiert. Andere werden hoffen, durch kleinere Modifikationen könne Kants Idee des a priori gerettet werden. Ich widerspreche dem. Die Vorstellung, wir hätten a priori Informationen, ist grundsätzlich falsch und führt nur zu einer vorgekaukelten Sicherheit.

Natürlich können wir aus dem anthropischen Prinzip Schlüsse über unsere Welt ziehen. Dabei handelt es sich aber nicht um Urteile a priori, sondern um Schlüsse, die wir aus der Beobachtung ziehen, dass wir bewusst denkende Lebewesen sind. Weiter ist natürlich richtig, dass jedes neugeborene Kind vor aller Erfahrung ein grosses Wissen über die Welt besitzt. Auch hierbei handelt es sich aber nicht um Urteile a priori, sondern um Schemata, die sich im Lauf der Evolution bewährt haben und die uns deshalb angeboren sind. Diese Schemata basieren also auch auf Erfahrung, wenn auch nicht auf persönlicher, so doch auf stammesgeschichtlicher, wie sie in der Evolutionären Erkenntnistheorie beschrieben wird (Con 1). Das Wissen, das uns so gegeben ist, ist keineswegs sicher. Im Gegenteil müssen wir gerade diese Schemata besonders kritisch hinterfragen, wie gerade die moderne Physik eindrücklich zeigt.

Wissen ist Information. Solange wir nicht wissen, woher diese Information stammt und worauf sie gründet, ist sie nicht gesichertes Wissen, und wir müssen ihr mit Skepsis begegnen. Es gibt genügend Gründe, selbst den Sinneseindrücken und den Experimenten zu misstrauen. Sicher sollten wir uns nicht darauf einlassen, an eine a priori Information zu glauben, nur weil wir uns mit unseren schwachen Geistern nichts anderes vorstellen können.

Insgesamt muss man sagen, Kants Erkenntnistheorie war ein Rückschritt gegenüber Humes. Bei Kant findet man keine Idee, wie Humes Zweifel beseitigt werden könnte. Sein einziges Argument ist der Aufruf an den blinden Glauben an ein a priori Wissen, das zumindest ich in mir drin nicht finde und an dem ich heftig zweifeln würde, wenn ich es finden würde. Kant schreibt zwar immer wieder, er habe bewiesen, wie a priori Erkenntnis möglich sei. Aber diesen Beweis gibt es nicht. Man findet ihn auch in der Sekundärliteratur nicht und auch nicht bei Kants sehr fleissigen Schülern. Kant hat für kein einziges synthetisches Urteil a priori gezeigt, dass es sicher gilt.

Kant begeht die Erzsünde, den Zweifel abzulegen und etwas als gesichert anzunehmen, wovon er höchstens vage Hinweise hat. Dadurch, dass er den Zweifel ablegt, kann er seine Irrtümer nicht mehr korrigieren. Wer alles schon besser weiss, kann nichts mehr dazulernen. Dies ist der Fehler aller totalitären Gruppierungen. Kant mag seiner Zeit ein Aufklärer gewesen sein. Heute brauchen wir eine zweite Aufklärung.

Einstein schrieb hierzu (Ein 2) : “Begriffe und Begriffsysteme erhalten die Berechtigung nur dadurch, dass sie zum Überschauen von Erlebniskomplexen dienen; eine andere Legitimation gibt es für sie nicht. Es ist deshalb nach meiner Überzeugung eine der verderblichsten Taten der Philosophen, dass sie gewisse begriffliche Grundlagen der Naturwissenschaft aus dem der Kontrolle zugänglichen Gebiete des Empirisch-Zweckmäßigen in die unangreifbare Höhe des Denknotwendigen (Apriorischen) versetzt haben. … Dies gilt im Besonderen auch von unseren Begriffen über Zeit und Raum, welche die Physiker – von Tatsachen gezwungen – aus dem Olymp des Apriori herunterholen mussten, um sie zu reparieren und wieder in einen brauchbaren Zustand setzen zu können.”

6. Wie die Physik a priori aufgebaut werden könnte

6.1. Holger Lyre und C. F. von Weizsäcker

Ich muss hier erwähnen, dass ich es durchaus für möglich halte, dass wir einmal a priori, also ohne uns auf Experimente zu berufen, eine Physik aufbauen können. Allerdings nur, wenn wir das in Abschnitt 5 Gesagte ernst nehmen und uns bewusst sind, dass eine Physik a priori keine Information enthalten kann. Jeder Versuch, in diese Physik a priori Information zu stecken, bedeutet lediglich, einem unbegründeten Vorurteil anzuhängen. Wenn wir aber genau analysieren, was ein System ohne Information bedeutet, so sehen wir, dass dieses System (fast?) alle wichtigen Naturgesetze automatisch enthält.

C.F. von Weizsäcker hat mit seiner Urtheorie hierzu einen Grundstein gelegt. Holger Lyre und andere haben basierend auf diesem Ansatz bemerkenswerte Erkenntnisse gewonnen (Lyr 1), (Cas 1), (Wei 2). Auch wenn Holger Lyre Kants Bedeutung völlig anders beurteilt als ich oben, stimme ich seinem Artikel (Externer Link: “Kann moderne Physik a priori begründbar sein?”) fast vollständig zu.

Lyre betont, durch Kants Theorie Erkenntnisse gewonnen zu haben, die für seine Arbeit von ausserordentlicher Bedeutung waren. Wenn jemand wie Lyre dies von sich selber behauptet, wäre es absurd zu widersprechen, zumal ja sein Ansatz gerade auf diesem Gebiet durchaus überzeugend ist. Gerade weil der Ansatz so überzeugend ist und sich unsere Einschätzung von Kants Werk so stark unterscheiden, erlaube ich mir einige Bemerkungen dazu.

Erstens können die Begriffe ‚notwendig‘ und ‚mit apodiktischer Gewissheit‘, die in Kants Philosophie an prominenter Stelle auftauchen, auf zwei unterschiedliche Arten gelesen werden. Lyre diskutiert in diesem Zusammenhang die höchst erstaunliche Tatsache, dass die Naturgesetze notwendig zu gelten scheinen. Sie gelten immer und überall und nicht nur mit sehr hoher Wahrscheinlichkeit. Steine fallen immer hinunter. So sieht es zumindest aus. Dieses bemerkenswerte Phänomen der Physik gilt es zu klären. Warum erscheinen uns die Naturgesetze als unausweichlich und allgemeingültig?

Kant dagegen aber verwendet die Begriffe ‚notwendig‘ und ‚mit Gewissheit‘ sehr oft, wenn er die Urteile a priori von Wahrscheinlichkeitsaussagen abgrenzen will, wie sie aus der Erfahrung gewonnen werden können. Kant hält das Wissen, das ihm a priori gegeben sei, für absolut gesichert. Nur so kann er nämlich behaupten, er habe Humes Zweifel überwunden.

Bemerkenswerterweise verwirft Lyre Kants ‚dogmatische Inanspruchnahme der unbezweifelbaren Evidenz eines Apriori‘. Er fordert einen Apriorismus ohne Dogmatismus. Kants Idee reduziert sich dann auf das, was ich Beobachter Regel nenne. In Lyres Worten: „Die wahren Bedingungen der Möglichkeit von Erfahrung können sich niemals empirisch als falsch erweisen – das wäre ein Widerspruch.“

Wenn wir umgekehrt fragen, wie den Lyre auf die Idee kommt, die Naturgesetze gelten notwendig, so wird klar, dass er sich keineswegs auf ein a priori Wissen stützt. Im Gegenteil basiert diese Idee auf seiner Erfahrung, was Kant für völlig unmöglich hält und klar verwirft. Lyre schreibt dazu: „Gerade als Physiker wird man nicht umhin können, das Bestechende dieses Arguments zu loben, denn die Unausweichlichkeit physikalischer Grundgesetze ist ein staunenswertes Urerlebnis eines jeden Naturwissenschaftlers.“ Lyre bezieht also das Wissen um die Allgemeingültigkeit der Naturgesetze aus der Erfahrung und ist sich dabei durchaus bewusst, dass sich dieses `Wissen´ auch als Irrtum erweisen kann, dass also Experimente dies als Vorurteil entlarven könnte.

6.2. Was können wir a priori wissen?

Schlussfolgerungen nach der Beobachter Regel

Die Frage ist, wie wir die wahren Bedingungen der Möglichkeit von Erfahrung finden können. Dass Kant dabei so spektakulär gescheitert ist, soll uns eine Warnung sein (auch in diesem Punkt stimme ich Lyre voll zu, und dies ist auch der Grund, weshalb ich die Kritik so scharf formuliert habe).

Wenn wir die Physik a priori begründen wollen, können wir uns auf die Beobachter Regel stützen, so wie Lyre dies vorschlägt. Meiner Ansicht nach ist dies aber nicht wirklich a priori. Ich nehme wahr, dass ich ein beobachtendes Lebewesen bin. Aus dieser Wahrnehmung kann ich sehr viel schliessen. Ich stütze mich dabei aber auf eine Beobachtung, nicht auf ein a priori Wissen. Wenn ich aus dieser Beobachtung etwas auf die Zukunft schliessen kann, dann nur deshalb, weil der Schluss von Erfahrungen auf die Zukunft eben durchaus möglich ist, wie ich im Artikel zum Induktionsprinzip zeige.

Lyre macht den Vorschlag, mit den Begriffen Unterscheidbarkeit und Zeitlichkeit zu beginnen, weil ohne Unterscheidbarkeit und Zeitlichkeit keine Erkenntnis möglich wäre. Er schreibt dazu z. B.: „Wer also weiss, was Erfahrung ist, oder von ihr methodisch Gebrauch macht, macht stillschweigend von der Zeitlichkeit im Sinne eines Unterschiedes von Vergangenheit und Zukunft Gebrauch. Wiederum wäre es nicht einmal möglich, Erfahrung zu definieren, ohne auf diesen Unterschied, ohne auf Zeitlichkeit zu rekurrieren.“

Auch hier müssen wir uns aber bewusst sein, dass wir den Begriff der Zeitlichkeit zwar im Sinne der Beobachter Regel voraussetzen können, aber keineswegs als Kantsches a priori. Wir können nach der Beobachter Regel schliessen, dass es eine Zeit geben muss, weil wir die Welt beobachten. Wir dürfen aber nicht wie Kant glauben, jedes Lebewesen, das Erfahrungen sammeln kann, müsse a priori über ein theoretisches Wissen verfügen, was Zeit ist. Viele Tiere können Erfahrungen sammeln und lernen, ohne zu wissen, was Zeit ist. Meine dreijährige Tochter weiss schon sehr viel über die Welt und kann sich sehr gut ausdrücken, aber sie hat nur eine sehr vage Vorstellung von der Zeitlichkeit. Alle Ereignisse der Vergangenheit waren für sie „gestern einmal“. Andere Zeitangaben versteht sie nicht. Wenn wir für die Zukunft einen Ausflug planen, sagt sie: „Wir gehen einmal …“ (Allerdings gibt es im Schweizerdeutschen keine Zukunftsform bei den Verben.)

6.3. Grundriss einer Physik a priori

Im Artikel Wie ist die Welt entstanden? skizziere ich, wie eine Physik a priori aussehen könnte. Ich bin der Ansicht, dass die Physik, ähnlich wie Holger Lyre es vorschlägt, a priori aufgebaut werden kann, allerdings mit einer entscheidenden Einschränkung: Die a priori aufgebaute Physik enthält null Information! Wenn sie denn jemals verwirklicht wird, ist sie also etwas völlig anderes als Kant es sich vorgestellt hat. Dies aus drei Gründen:

Erstens mache ich genau das Gegenteil von dem, was Kant macht: Ich setze a priori voraus, dass wir kein a priori Wissen haben.

Zweitens bin ich nach wie vor auf die Erfahrung angewiesen. Auch wenn ich alle Formeln präzise aufschreiben könnte, muss ich im Experiment überprüfen, ob sie in unserer Welt gelten. Denn möglicherweise gelten in verschiedenen Welten verschiedene Naturgesetze oder die Naturgesetze ändern sich sogar in unserer Welt. Manche, ernst zu nehmende Leute, haben sogar vorgeschlagen, das Universum könnte in sich widersprüchlich sein.

Wir können die Naturgesetze experimentell überprüfen, was Kant abstritt. Gestützt auf Erfahrung sind Aussagen über die Zukunft möglich, wie ich im Artikel zum Induktionsprinzip zeige.

Drittens beruhen unsere Schlüsse im Alltag nicht auf diesen a priori Überlegungen. Die Menschen auf der Strasse stützen sich bei ihren Aussagen über die Natur nicht auf das a priori Wissen. Wenn jemand sagt, die Sonne werde morgen wieder aufgehen, dann weiss er dies aus Erfahrung und nicht dank irgendeines a priori Wissens. Selbst wenn es einmal gelingt, so eine Physik a priori aufzustellen, so würden die meisten Menschen diese komplizierte und sehr abstrakte Theorie überhaupt nicht kennen, geschweige denn verstehen.

7. Weiterführende Literatur

Weiterführende Artikel:

Wie ist die Welt entstanden?
Was ist Realität?
Das Induktionsprinzip
Falsifizierbarkeit

Weiterführende Bücher:

Kant Immanuel, ‘Kritik der reinen Vernunft’, Reclam

Kant Immanuel, ‘Prolegomena zu einer jeden künftigen Metaphysik, die als Wissenschaft wird auftreten können’, Reclam