Visits: 1585
Philipp Wehrli, 2. Januar 2002
Das Doppeltspaltexperiment könnte zumindest auf den ersten Blick auch klassisch erklärt werden. Wir könnten sagen: Wenn die Elektronenkanone ein Elektron abschiesst, so geht von der Kanone gleichzeitig auch eine Welle aus. Das Elektron schwimmt auf dieser Welle mit und kann sich nur da bewegen, wo auch die Welle ist. Es ist aber ein Teilchen und befindet sich zu jedem Zeitpunkt genau an einem Ort. David Bohm und Louis deBroglie haben mit einigem Erfolg versucht, eine solche Theorie der ‘Führungswelle’ zu formulieren (Spe 1). Das hier beschriebene Experiment widerlegt die Theorie der Führungswellen.
Erst 1992 gelang es, mit einem Experiment nachzuweisen, dass eine Welle ohne Teilchen nicht existiert oder zumindest nicht messbar ist. Das Experiment ist ziemlich trickreich. Aber es ist so wunderschön, dass ich es hier einfach vorstellen muss! Wer vor einer etwas komplizierten Versuchsanordnung nicht zurückschreckt, findet hier einige wichtige Anhaltspunkte, was an der Quantenwelt ‘real’ ist und was mathematisches Beigemüse. Zunächst einmal bauen wir den ‘Doppelspaltversuch’ etwas moderner. Ausserdem verwenden wir dazu diesmal Photonen, also Lichtteilchen. Photonen haben wie Elektronen eine bestimmte Wellenlänge. Diese Wellenlänge ist umso kürzer, je grösser die Energie des Photons ist.
Bei diesem ‘Doppelspaltversuch’ benützen wir zwei grundsätzlich verschiedene Arten, ein Photon in zwei Teilstrahlen zu zerlegen. Bei der ersten Art wird das Photon auf einen doppelbrechenden Kristall geschossen. Dieser wandelt das Photon in zwei Photonen von je halber Energie, also mit doppelt so langer Wellenlänge um.
Abbildung 1 Wird ein Photon auf einen doppelbrechenden Kristall geworfen, so spaltet es sich in zwei Photonen mit doppelter Wellenlänge auf.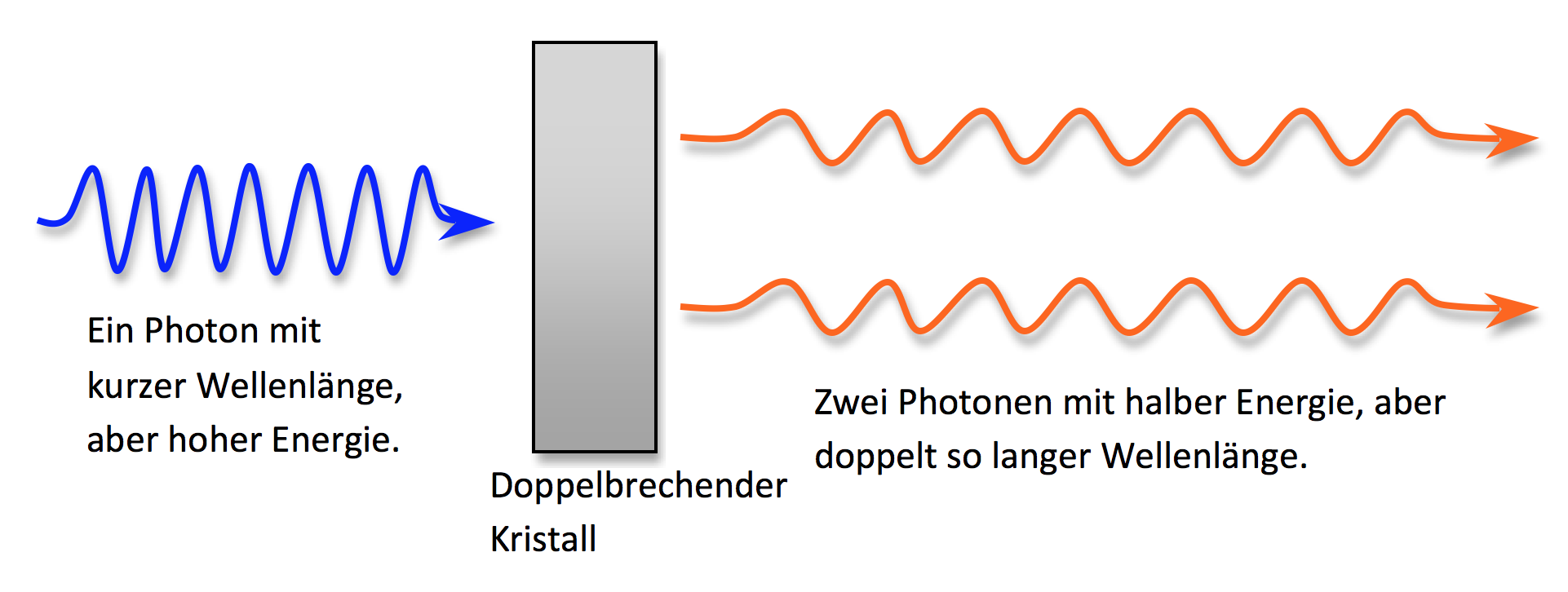
Bei der zweiten Art wird ein Photon aus einem Laser an einem halbdurchlässigen Spiegel in zwei Teilwellen gespalten, die sich gegenseitig überlagern und interferieren können. Das Photon kann also wie im Doppelspalt zwei verschiedene Wege gehen und wie im Doppelspaltexperiment geht es gewissermassen beide Wege gleichzeitig. Es ist aber nur ein Photon.
Im Versuch spalten wir ein Photon mit einem sogenannten Strahlteiler, einem halbdurchlässigen Spiegel (½ Spiegel) in zwei Teilwellen A und B (Abbildung 2). Den ersten Weg geht die Teilwelle A (dunkelgrau). Sie trifft auf einen doppelbrechenden Kristall K1 und wird dort wie beschrieben in ein Photonenpaar A1 und A2 umgewandelt (dunkelgrau gestrichelt). Bohr hätte gesagt: „Diese neuen Photonen sind ebenfalls Teil des einen möglichen Weges. Wie beim Doppelspalt existieren sie nur, wenn ich nachschaue und sehe, dass sie existieren.“
Den zweiten Weg geht die Teilwelle B (hellgrau). Sie trifft auf einen anderen doppelbrechenden Kristall K2, wird dortin ein Photonenpaar B1 und B2 umgewandelt (hellgrau gestrichelt), und zwar genau in dem Moment, in dem die Teilwelle A2 den Kristall K2 kreuzt.
Wenn die Teilstrahlen A2 und B2 zusammengeführt werden und ebenso die Teilstrahlen A1 und B1 so lässt sich nicht mehr bestimmen, ob der Weg A oder B gewählt wurde. Weil der Weg nicht mehr bestimmt werden kann, kommt es zwischen A1 und B1 zu einem Interferenzmuster.
Abbildung 2 Ein realistisches Doppelspalt-Experiment. Details im Text.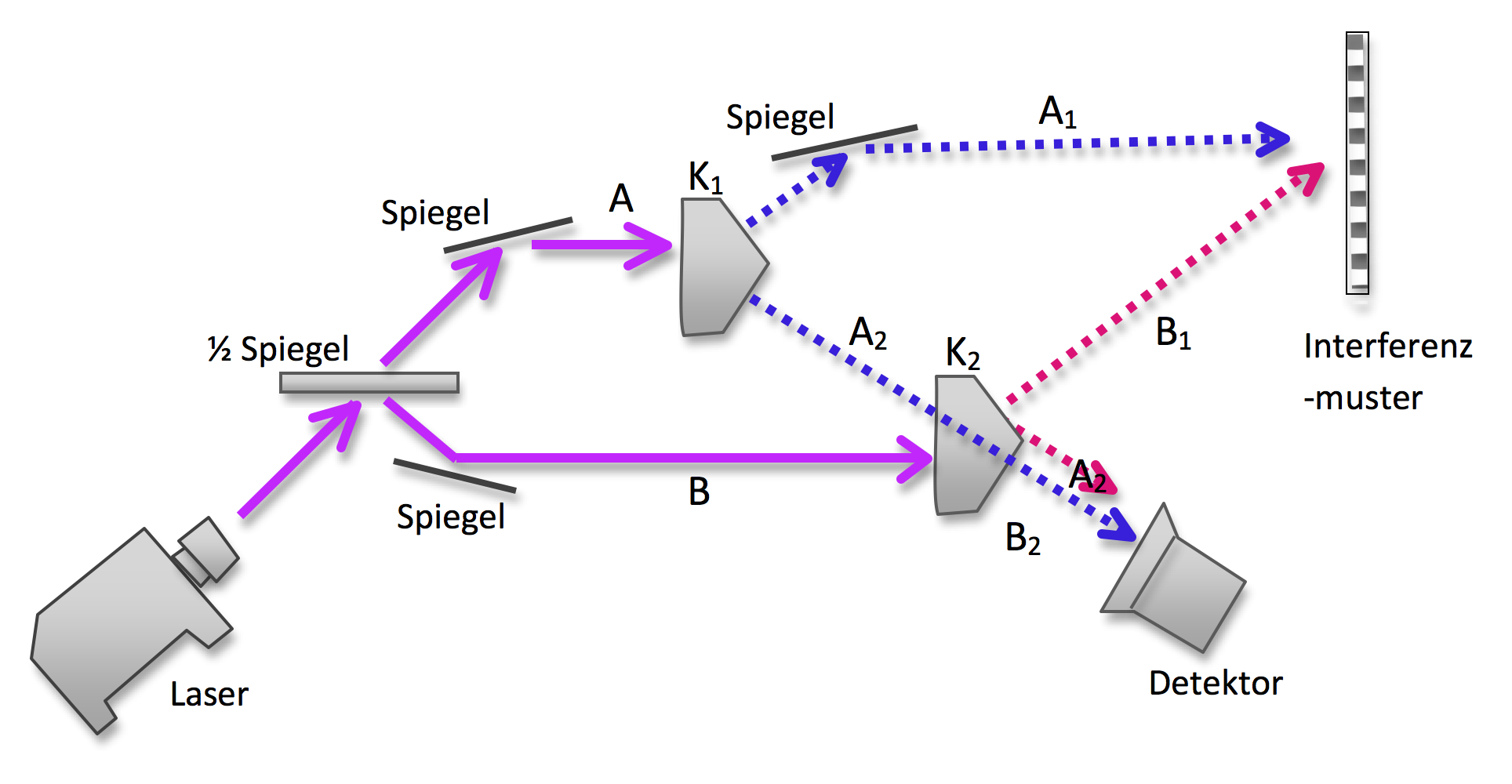
Es ist ganz entscheidend, dass A2 gleichzeitig mit B auf den Kristall trifft. Denn die Wellen B1 und B2 übernehmen von A2 den Takt (die Phase), in dem sie schwingen. Ohne A2 würden sie zu einem beliebigen Zeitpunkt zu schwingen beginnen und B1 könnte nicht mit A1 interferieren. A2 wird während dieses ‘Taktgebens’ zwangsläufig mit B2 überlagert, deshalb gibt es in diesem Strahl kein schönes Interferenzmuster.
Wenn wir verhindern, dass der Teilstrahl A2 den Strahlen B1 und B2 den Takt angibt, verschwindet das Interferenzmuster. Dies können wir z. B. dadurch tun, dass wir den Weg zwischen den Kristallen K1 und K2 versperren. Nun sehen wir aber mit dem Detektor, ob Weg A oder B verwirklicht wurde. Denn der Detektor misst genau dann ein Photon, wenn der Weg B gewählt wurde. Wieder gilt die Grundregel der Quantenmechanik: Wenn der Weg bestimmt werden kann, kann es keine Interferenz mehr geben. Also interferieren auch die Teilstrahlen A1 und B1 nicht mehr.
Wenn wir auf irgendeine Weise herauszufinden versuchen, ob im Teilstrahl A2 ein Photon drin ist, dann verhindern wir dadurch zwangsläufig, dass der Teilstrahl A2 den Strahlen B1 und B2 den Takt angibt.
Abbildung 3 Wenn wir den Weg A2 versperren, können wir herausfinden, welchen Weg das Photon gewählt hat. Es gibt keine Interferenz.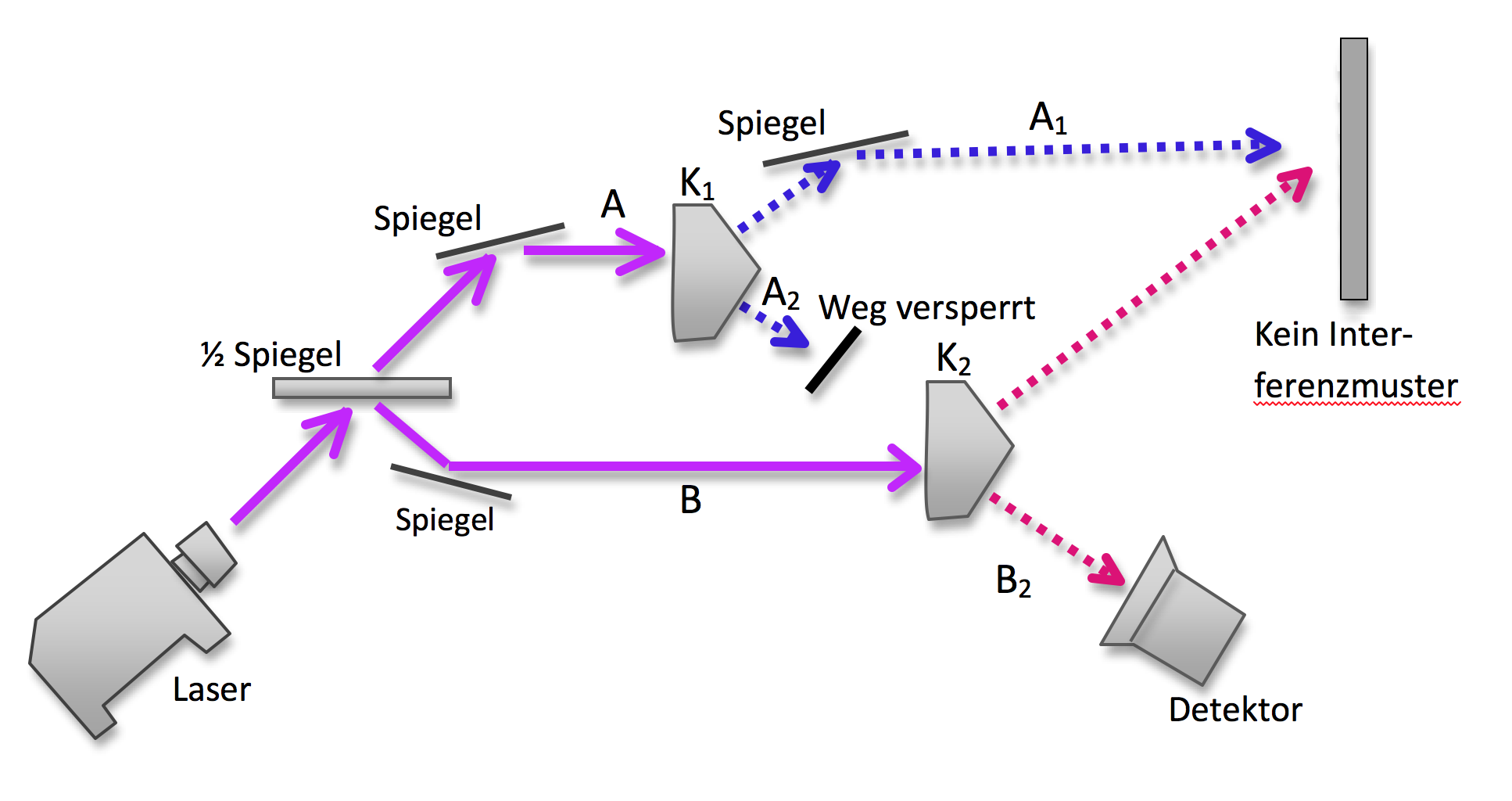
Auch dieses Experiment ist mit der Theorie der Führungswelle erklärbar. Nach deBroglies Theorie braucht es aber gar kein Teilchen, um im Kristall K2 den Takt anzugeben. Schon eine leere Welle müsste dazu reichen. Ob dies wirklich geschieht, kann in einem leicht abgeänderten Versuch nachgeprüft werden (Zou 1) (siehe Abbildung 4).
Statt den Strahl A2 völlig abzufangen, wird er durch einen halbdurchlässigen Spiegel geschickt. Nach deBroglie kann nun das Photon entweder durch diesen Spiegel hindurchgehen oder es kann von ihm zu einem zweiten Detektor 2 abgelenkt werden. Aber auch wenn es abgelenkt wird, geht ein Teil der Führungswelle immer durch den halbdurchlässigen Spiegel hindurch. Nach der Theorie der Führungswellen müsste diese leere Welle ausreichen, um den Strahlen B1 und B2 den Takt anzugeben und Interferenz zwischen A1 und B1 zu erzeugen.
Abbildung 4 Wird in Detektor 2 ein Photon gemessen, dann kreuzen sich nach deBroglies Theorie in K2 zwei leere Führungswellen. Es zeigt sich, dass diese ‚leeren Führungswellen’ zumindest in dieser Anordnung nicht zu einem Interferenzmuster führen. Ob sie ‚existieren’ mag jeder selbst entscheiden.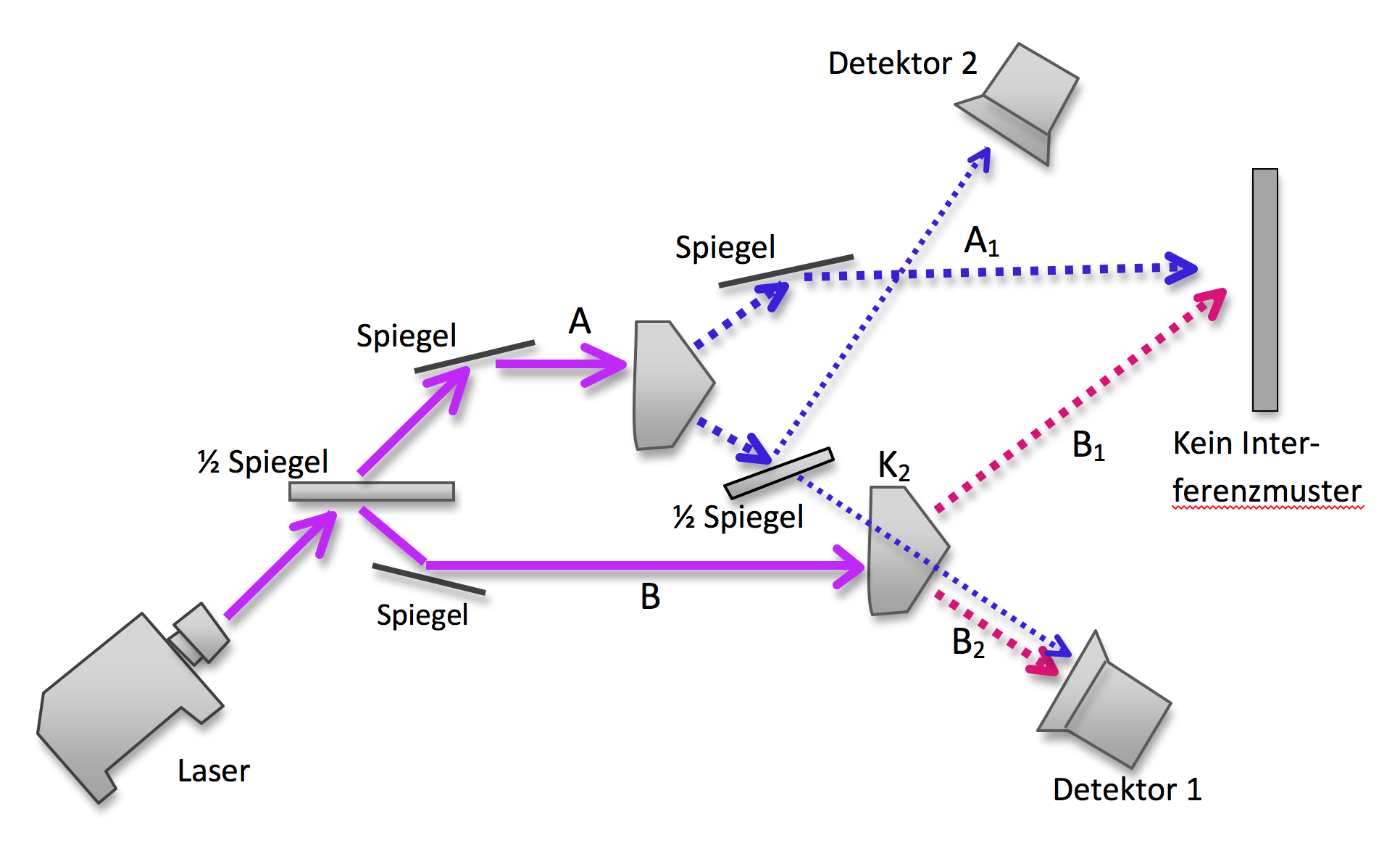
Wir schiessen nun mit dem Laser einzeln Photonen auf den Weg. Immer wenn wir beim Detektor 2 ein Photon messen, wissen wir, dass sich in K2 zwei leere Wellen kreuzen. Daraus schliessen wir, dass gleichzeitig in der Welle A1 ein Photon mitschwimmt. Wir schauen, ob in diesen Fällen zwischen A1 und der leeren Welle B1 eine Interferenz auftritt. Dies ist nicht der Fall. Eine Welle, die mit Sicherheit leer ist, hat keinen Einfluss auf das Experiment. Ob wir von so einer Welle sagen sollen, sie ‘existiere’, mag der Leser selber entscheiden.
Vielleicht denken Sie, die Welle, die durch den halbdurchlässigen Spiegel hindurch geht, ist einfach zu klein geworden, um noch eine sichtbare Wirkung zu haben. Aber wir könnten den Spiegel auch viel durchsichtiger machen und z. B. 99 % der Welle hindurchlassen. Dann würden wir im Detektor 2 zwar nur selten ein Photon registrieren. In diesen Fällen wüssten wir aber, dass eine sehr grosse, aber mit Sicherheit leere Welle über den Kristall K2 gegangen ist. Auch mit diesem Experiment kann keine Interferenz erzeugt werden. Bisher gilt für alle durchgeführten Experimente: Wenn ich weiss, welchen Weg ein Teilchen geht, gibt es keine Interferenz.
Im Artikel Viele-Welten-Interpretation zeige ich, dass es durchaus Gründe für die Annahme gibt, die leere Welle existiere.
Weiterführende Artikel auf dieser Homepage:
Doppelspaltversuch
Der Beobachter in der Quantentheorie
Der Quantenradierer
Weiterführende Bücher:
Philip Wehrli, ‘Das Universum, das Ich und der liebe Gott’, (2017), Nibe Verlag,

In diesem Buch präsentiere ich einen Gesamtüberblick über mein Weltbild: Wie ist das Universum entstanden? Wie ist das Leben auf der Erde entstanden? Was ist Bewusstsein und woher kommt es? Braucht es dazu einen Gott?
Viele Artikel dieses Blogs werden in diesem Buch in einen einheitlichen Rahmen gebracht, so dass sich ein (ziemlich) vollständiges Weltbild ergibt.
Leserunde bei Lovelybooks zum Buch ‘Das Universum, das Ich und der liebe Gott’, von Philipp Wehrli (abgeschlossen)
Rezensionen bei Lovelybooks
Rezensionen bei Amazon
Film-Präsentation zum Buch
Nibe Verlag
Audretsch Jürgen / Mainzer Klaus (Hrsg), ‘Wieviele Leben hat Schrödingers Katze?’, Spektrum Akademischer Verlag, (1990), Heidelberg / Berlin / Oxford
Verschiedene Autoren interpretieren die Quantentheorie anhand der aktuellen Experimente. Sehr anregend. Die entscheidenden Argumente sind aber nur nachvollziehbar, wenn man die Quantentheorie schon kennt und vor mathematischen Formeln nicht zurückschreckt.
Paul Harry, ‘Photonen- Eine Einführung in die Quantenoptik’, (1999), Teubner Studienbücher, Leipzig
Etwas vom Besten, was zur Quantentheorie geschrieben wurde! Paul stellt die schönsten Experimente der Quantenoptik vor und analysiert scharfsinnig, weshalb die klassische Physik versagen muss. Die ideale Einführung für alle, die nicht nur rechnen, sondern die Natur auch verstehen wollen. Benützt nur sehr einfache Mathematik.
Selleri Franco, (1990) ‘Die Debatte um die Quantentheorie’, Vieweg, Braunschweig
Sellerie zeigt die Interpretationsprobleme, die durch die Quantentheorie aufgeworfen wurden und erklärt, wie sie von den Begründern der Theorie gelöst wurden und wie die Interpretationen heute z. T. mit Experimenten überprüft werden können. Dabei verwendet er ziemlich abstrakte Mathematik. Man kann zwar über die meisten Formeln hinweglesen, aber das Buch verliert dabei natürlich etwas.
Spektrum Akademischer Verlag, Heidelberg, ‘Quantenphilosophie – Reihe Verständliche Forschung’, Neuser / Neuser-von Oettingen (Herausgegeber)
Wer sich für die Philosophie hinter der Quantentheorie interessiert, findet hier ein breites Spektrum anregender Artikel, unter anderem von Schrödinger, Gamov, d´Espagnat, Cassidy und de Witt. Die Artikel sind kurz, prägnant und allgemeinverständlich und werden mit vielen schönen Grafiken illustriert.
