Visits: 3992
Philipp Wehrli, 18. Oktober 2006
Wenn von der allgemeinen Relativitätstheorie und von gekrümmten Räumen gesprochen wird, fragen sich Laien häufig: “Wenn der Raum gekrümmt ist, muss es doch einen Aussenraum geben? Wieso sehen wir den Aussenraum nicht?“ Ich versuche hier in einfachen Worten die Idee der gekrümmten Geometrie zu erklären.
Das Universum ist der gesamte Raum. Es gibt keinen Aussenraum. Das ist schwer zu glauben. Wenn in der allgemeinen Relativitätstheorie von Krümmung gesprochen wird, so ist damit nie die Krümmung in einen Aussenraum gemeint. Vielmehr kann ein Raum auch in sich selber gekrümmt sein. Dies war die grosse Erkenntnis, die Friedrich Gauss in seinem theorema egregium, dem ‚herausragenden Theorem’ formulierte: Es gelang ihm, den Begriff Krümmung so zu definieren, dass kein Aussenraum nötig ist. Wenn ein Plattwurm auf einer gekrümmten Ebene umher kriecht und nichts vom Rest der Welt wahrnimmt, kann er doch feststellen, dass die Ebene gekrümmt ist.
Aber weshalb war Gauss so begeistert von diesem Satz, dass er ihn das ‚herausragende Theorem’ nannte? –Das Schöne ist, dass eine Beschreibung ohne Aussenraum das Charakteristische des beschriebenen Gegenstandes viel besser einfängt, als eine Beschreibung mit Aussenraum.
Betrachten wir z. B. einen Strumpf. Ein Strumpf ist ein zweidimensionaler gekrümmter Raum. Ich kann den Strumpf im dreidimensionalen Raum beschreiben. Dazu würde ich zu jedem Punkt im dreidimensionalen Raum angeben, ob da Strumpf ist oder nicht.
Wie könnte ich den Strumpf beschreiben, ohne den Aussenraum zu benützen? Ich tue dies genau so, wie ein Strumpf zusammengeknöpft werden könnte (Handarbeitslehrerinnen bitte weghören). Wenn wir eine Anleitung aufschreiben müssen, von wo nach wo die Fäden gehen, so müssen wir zu jedem Punkt für die x- und die y-Richtung angeben, in welchem Abstand der nächste Faden angeknöpft wird. Ausserdem brauchen wir eine Zahl, welche die Länge der Diagonalen festlegt, also z. B. von (0/0) nach (1/1). Ein zweidimensionales Gitternetz ist also definiert, wenn ich in jedem Punkt drei Zahlen angebe.
Abbildung 1 Wie ein gekrümmter Raum beschrieben wird.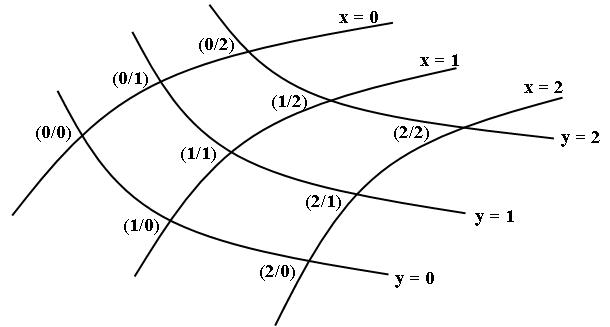
Wenn zwei verschiedene Leute diese Anleitung befolgen, so sehen die zwei Strümpfe für eine Ameise, die darauf herumkrabbelt, genau gleich aus. Die Ameise sieht, wie in welchem Rhythmus sie auf Kreuzungen stösst. Im dreidimensionalen Raum sehen die Strümpfe aber vielleicht völlig unterschiedlich aus.
Ein Strumpf kann zerknittert in einer Wäschetrommel liegen, er kann an einer Wäscheleine hängen oder er kann sorgfältig zusammengefaltet in einem Schrank sein. Im dreidimensionalen Raum würde man denselben Strumpf auf unendlich viele so völlig verschiedene Arten beschreiben, dass untereinander überhaupt keine Ähnlichkeit mehr bestehen würde. Wenn ich den Strumpf aber zweidimensional beschreibe, wie oben das Drahtgitter, dann bleibt die Beschreibung immer gleich, egal ob der Strumpf zerknittert ist oder nicht. Die zweidimensionale Beschreibung, also die Beschreibung ohne Aussenraum zeigt also die Charakteristik des Strumpfs besser und sie ist auch in gewissem Sinne einfacher. Denn in der Beschreibung ohne Aussenraum gibt es nur den Strumpf und der Strumpf hat nur genau einen Zustand. Diese Entdeckung muss Gauss begeistert haben: Mit weniger Aufwand, nämlich mit nur zwei statt drei Dimensionen, kann ich die Charakteristik einer gekrümmten Fläche besser einfangen, als wenn ich den grösseren Aufwand betreibe. Gauss war überzeugt, dass er mit diesem Satz nicht nur einen mathematischen Zusammenhang gefunden, sondern eine fundamentale Eigenschaft des realen Raumes entdeckt hatte.
Die Art, wie Gauss gekrümmte Räume beschrieb, ist in gewissem Sinne eleganter und einfacher als die flache euklidische Geometrie, die wir kennen. ‚Einfacher’ heisst hier nicht ‚leicht verständlich’. Eine Theorie ist ‚einfach’, wenn sie nur auf wenige Axiome aufbaut, wenn nur wenige unbegründete Annahmen vorausgesetzt werden. Die flache Geometrie ist nur ein Spezialfall der gekrümmten. Sie ist komplizierter, denn für eine flache Geometrie brauche ich alle Axiome der gekrümmten Geometrie, zusätzlich aber noch das Axiom, dass die Krümmung null ist.
Wie erkenne ich, ob ein Raum gekrümmt ist?
Gauss zeigte, wie man nur aufgrund der Abstände und Winkel im Raum merken kann, ob ein Raum gekrümmt ist. Die mathematischen Details führen hier zu weit (siehe dazu (Olo 1) ). Ganz grob kann man sagen, dass in einem gekrümmten Raum die euklidsche Geometrie nicht gilt. Die Winkelsumme in Dreiecken muss nicht mehr 180° betragen. Ein Kreis mit Radius r hat nicht zwingend einen Umfang von 2rπ usw.
Abbildung 2 Die Winkelsumme eines Dreiecks im gekrümmten Raum muss nicht unbedingt 180° betragen.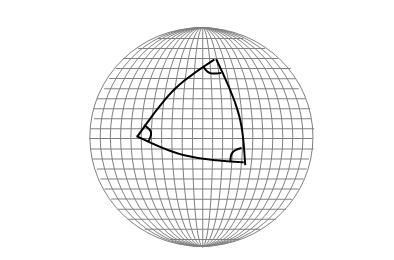
Die Abbildung 2 zeigt noch ein Charakteristikum gekrümmter Räume. Es ist im Allgemeinen nicht möglich, einen gekrümmten Raum mit einem einzigen brauchbaren Koordinatensystem zu überziehen. Schon beim einfachen Fall einer Kugel ergeben sich Probleme. Z. B. ordnet das Koordinatensystem in Abbildung 2 dem Nord- und dem Südpol der Kugel keine eindeutigen Koordinaten zu, denn die Pole liegen auf allen Längengraden gleichzeitig. Probleme solcher Art sind gemeint, wenn gesagt wird, irgendein Gesetz „gilt nur lokal“, „ein Inertialsystem lässt sich nur lokal definieren“, der Energie bleibt „nur lokal erhalten“ oder „Überlichtgeschwindigkeiten sind lokal nicht möglich“.
Gemeint ist immer: Ein kleiner Teil des gekrümmten Raumes muss ausgewählt werden, wie eine Karte von einem kleinen Ausschnitt der Erdoberfläche problemlos und ohne grosse Verzerrungen gezeichnet werden kann. In diesem kleinen Bereich, der (praktisch) ohne Verzerrungen abgebildet werden kann, gilt dann der jeweilige Satz.
Ein Raum ist genau dann gekrümmt, wenn die euklidische Geometrie nicht gilt. Viele Flächen, die auf den ersten Blick gekrümmt aussehen, sind mathematisch gesehen flach, haben also Krümmung null. Ein Beispiel eines flachen Raumes zeigt Abbildung 3. Jede Papierrolle ist flach, denn allfällige geometrische Figuren auf dem Papier gehorchen den Gesetzen der euklidischen Geometrie.
Abbildung 3 Die euklidische Geometrie gilt auf der ganzen abgebildeten Fläche, deshalb hat diese Fläche die Krümmung null.
Um einen zweidimensionalen gekrümmten Raum zu beschreiben, brauche ich also drei Zahlen in jedem Punkt des Raumes, nämlich auf jeder Achse eine Zahl für den Abstand zur nächsten Koordinate und eine Zahl für den Zwischenwinkel. In der vierdimensionalen Raumzeit brauche ich für alle vier Dimensionen je eine Zahl für den Abstand zur nächsten Koordinate. Ausserdem gibt es zwischen je zwei Achsen einen Winkel. Zu den vier Achsen x, y, z, t gibt es sechs Zwischenwinkel: (x, y), (x, z,) (x, t), (y, z), (y, t), (z, t). Insgesamt sind in der allgemeinen Relativitätstheorie also in jedem Punkt der Raumzeit 10 Zahlen nötig, um die gesamte Raumzeit zu beschreiben. Wenn ich durch die Raumzeit wandere, ändern sich diese zehn Zahlen, und aus der Art, wie sie sich ändern, können wir berechnen, ob der Raum gekrümmt ist und falls ja, wie stark.
Die Zahlen sagen etwa: „In x-Richtung kommst du nur mühsam voran“, „In y-Richtung geht es leicht“, „Hier verrinnt die Zeit wie im Flug“. Was wir als gerade empfinden, hängt von diesen Zahlen ab. Gerade ist sozusagen der schnellste Weg zwischen zwei Punkten. Wenn ich in einem Sumpf nur langsam vorwärts komme, so mache ich einen Bogen um den Sumpf herum. In der Raumzeit erscheint mir dies aber nicht als Umweg, sondern als die kürzeste Verbindung. Diese anschaulichen Vergleiche sollen zeigen, dass mit Krümmung nicht eine Krümmung in einen äusseren Raum gemeint ist.
Weshalb glauben Physiker nicht an einen äusseren Raum?
Könnte es nicht sein, dass unser Raum in einen äusseren Raum hinein gekrümmt ist? Wir sehen diesen äusseren Raum zwar nicht, aber er ist ja vielleicht doch da?
Wir können nie beweisen, dass etwas, was wir nicht sehen können, nicht existiert. Vielleicht gibt es Gespenster, niemand kann beweisen, dass es keine Gespenster geben kann. Wissenschafter halten sich in solchen Fragen an das Ökonomieprinzip. Sie fragen sich: Wird unser Weltbild einfacher, wenn ich an Gespenster glaube oder wird es komplizierter? Einfacher heisst hier wieder: Mein Weltbild basiert auf möglichst wenigen Annahmen, die ich nicht weiter begründen kann.
Ein äusserer Raum kann bis heute nicht beobachtet werden. Die Beschreibung mit äusserem Raum würde komplizierter, sie würde die Charakteristik des sichtbaren Raumes schlechter zeigen und würde mehr Axiome benötigen. Aus diesen Gründen ist es nicht sinnvoll zu glauben, dass der sichtbare Raum in einer zusätzlichen unsichtbaren Dimension in einen äusseren Raum hineingekrümmt ist. Wir brauchen den äusseren Raum nicht.
Weitere Artikel auf dieser Homepage zur allgemeinen Relativitätstheorie:
Ausgewählte Effekte der allgemeinen Relativitätstheorie (ART)
Wie kommt die Gravitationskraft zustande?
Externe Links:
Didaktisches Material und Animationen zur Relativitätstheorie
Weiterführende Bücher:
Um wirklich zu verstehen, wie man in der gekrümmten Geometrie rechnet, muss man Differentialgeometrie (Riemannsche Geometrie) studieren.
Nach einem Grundstudium Mathematik eignen sich z. B. (Olo 1) oder (Sex 4).
Einstein Albert, ‘Über die spezielle und die allgemeine Relativitätstheorie, gemeinverständlich’, Springer, (1916)
Nach wie vor eine der besten Einführungen in die Relativitätstheorie, das Werk von ihrem Schöpfer selbst.
Epstein Lewis C., ‘Relativitätstheorie anschaulich dargestellt’, Birkhäuser, (1983), Basel
Von diesem Buch bin ich begeistert! Ohne Mathematik zeigt Epstein, wie die Krümmung der Raumzeit zur Gravitationskraft führt, wie die Lichtablenkung an grossen Massen zustande kommt und wie schwarze Löcher funktionieren.
Oloff Rainer, ‘Geometrie der Raumzeit – Eine mathematische Einführung in die Relativitätstheorie’, (1999), Vieweg, Braunschweig
Das Buch ist geschrieben für Studenten der Mathematik oder Physik, die in einem einsemestrigen Kurs von zwei Doppelstunden plus Übungen die allgemeine Relativitätstheorie wirklich verstehen wollen. Oloff erklärt bei jeder Definition und jedem Satz, wozu er sie braucht. Die Erklärungen sind anwendungsorientiert und verständlich. Ein ausgezeichnetes Buch für Physikstudenten!
Kaku Michio, Im Hyperraum – Eine Reise durch Zeittunnel und Paralleluniversen, (1998), Rowohlt Taschenbuch Verlag GmbH
Vermischt mit vielen Anekdoten wird die Entwicklung der gekrümmten Geometrie in 4 und mehr Dimensionen erzählt und ihre Bedeutung für die Kosmologie und die Teilchenphysik erklärt. Leider erklärt Kaku die schwarzen Löcher falsch (mit der Entweichgeschwindigkeit, die nicht grösser als c sein darf) und die kosmische Rotverschiebung ebenfalls falsch als Dopplereffekt. Dennoch ein empfehlenswertes Buch.
Philip Wehrli, ‘Das Universum, das Ich und der liebe Gott’, (2017), Nibe Verlag,

In diesem Buch präsentiere ich einen Gesamtüberblick über mein Weltbild: Wie ist das Universum entstanden? Wie ist das Leben auf der Erde entstanden? Was ist Bewusstsein und woher kommt es? Braucht es dazu einen Gott?
Viele Artikel dieses Blogs werden in diesem Buch in einen einheitlichen Rahmen gebracht, so dass sich ein (ziemlich) vollständiges Weltbild ergibt.
Leserunde bei Lovelybooks zum Buch ‘Das Universum, das Ich und der liebe Gott’, von Philipp Wehrli (abgeschlossen)
Rezensionen bei Lovelybooks
Rezensionen bei Amazon
Film-Präsentation zum Buch
Nibe Verlag
Bei der Beschreibung einer gekrümmten Fläche gibt es ein riesen Problem. Was existiert zwischen zwei Punkten? Euklidisch ist die Antwort einfach, eine gerade Strecke.
Bei gekrümmten Flächen muss man die Krümmung kennen, Kugel. Man braucht also mehr Information als bei Euklid. Außerdem gehören zu einer gekrümmten Fläche nur bestimmte Punkte.
Euklid ist viel allgemeiner, hier gibt es nur Punkte und Strecken. Der Raum ist egal.
Wie sieht ein gekrümmter Raum mit 10 000 Dimensionen aus?
Wie kann aus einem Euklidischen Raum durch eine Masse plötzlich ein Nichteuklidischer Raum werden? Aus einer Fläche entsteht eine Kugeloberfläche? Auch in der Mathematik gibt es da ein Problem, eine Kugeloberfläche besteht nur aus Punkten. Punkte haben aber keine Fläche. Und Punkte existieren immer einzeln. Eine Strecke ist in der Mathematik eigentlich ein Kontinuum, also etwas eigenes, genauer eine Erfindung unseres Gehirns, das immer Dinge zusammenfasst, wenn es sie nicht einzeln speichern will. Der Kreis ist eine Erfindung unseres Gehirns. Unser Gehirn definiert aber solche Dinge nicht. Es ist ein Bild, das unser Gehirn so abspeichert. Erst Mathematiker wollten dann dieses Bild definieren. Ich glaube nicht, das Einstein je über so etwas nachgedacht hat.
Feynman sagt: Mathematik ist nicht Physik
Ich stimme ihm zu, das sind zwei grundsätzliche verschiedene Welten. Ob Einstein das auch so gesehen hat, kann man bezweifeln. Ich habe nie verstanden, wie eine Masse den Raum krümmen soll. Wie macht die Natur das? Diese Antwort hätte ich gern, egal von wem.
1.Was existiert zwischen zwei Punkten einer gekrümmten Fläche?
Unendlich viele Verbindungen, genau wie bei einer flachen Fläche.
Eine kürzeste bzw. geradeste Verbindung, genau wie bei einer flachen Fläche.
Flugzeuge fliegen transkontinental auf solchen Linien (sog. Geodäten)
2. Wie krümmt die Natur den Raum?
Gegenfrage, warum sollen sich sich 2 Massen anziehen? Das habe ICH nie verstanden.
Gedankenexperiment: Wenn die Sonne explodiert, dann verlässt nach Newton unsere Erde SOFORT ihre Bahn, aber erst 8 Minuten später wird es dunkel. Also funktioniert da mit Newton etwas nicht.
Warum fällt eine Feder genauso schnell wie ein Hammer im Schwerefeld des Mondes? (da gibt es keinen Luftwiderstand). Weil beide auf Linien des kürzesten Weges (Geodäten) im gekrümmten Raum , besser der Raumzeit fallen.
“Massen sagen, wie die Raumzeit sich krümmt, die Raumzeit sagt wie Massen sich darin bewegen”
Wie macht die Natur das? Das weiß keiner. Dafür sind wir nicht hoch genug entwickelt. Auf einer höheren Entwicklungsstufe (so etwas wie Supermensch) könnte man das vielleicht ganz einfach, ohne Mathematik, verstehen.