Visits: 3677
Philipp Wehrli, 7. Oktober 2007
Nach der allgemeinen Relativitätstheorie kann die Gravitation als eine Eigenschaft der gekrümmten Raumzeit angesehen werden. Weil die Zeit in der Nähe von Massen langsamer läuft, ziehen Massen sich an. In ähnlicher Weise kann auch die elektrische Kraft als eine Eigenschaft der Raumzeit interpretiert werden. Allerdings spielt bei der elektrischen Kraft die komplexe Phase der Wellenfunktion eine Rolle. Es wird nicht die Raumzeit gekrümmt, sondern es wird an jedem Punkt der Raumzeit die komplexe Phase gedreht.
Dieser Artikel setzt den Artikel Gravitation voraus.
Ziel dieser Abhandlung ist nicht, eine neue Theorie der Elektrizität zu schaffen, sondern die bestehende, mathematisch formulierte Theorie in ein anschauliches Modell zu übersetzen. Falls mein Modell in manchen Bereichen nicht ganz mit der üblichen Elektrodynamik übereinstimmt, ist selbstverständlich mein Modell in dieser Frage falsch, denn die Elektrodynamik stimmt bekanntlich ausgezeichnet mit allen Experimenten überein. Mein Modell ist aber sehr direkt dem Aufbau der Elektrodynamik als Eichtheorie nachempfunden, so dass Abweichungen höchstens in einigen Detailfragen eine Rolle spielen können.
Wohl die schönste Entdeckung der allgemeinen Relativitätstheorie ist, dass die Gravitation durch die Verlangsamung der Zeit in der Nähe von Massen vollständig erklärt wird. Die zwei scheinbar völlig verschiedenen Begriffe ‘Raumzeit’ und ‘Gravitationskraft’ werden damit in einen engen Zusammenhang gebracht. Da die elektrische Kraft nach dem Coulombgesetz grosse Ähnlichkeit mit der Gravitation aufweist, ist man versucht, sie in ähnlicher Weise zu erklären.
Tatsächlich kann die elektrische Kraft wie die Gravitation mit einer anschaulichen Erklärung auf Effekte der Raumzeit zurückgeführt werden. Ich zeige im Folgenden, wie die elektrische Kraft als sogenannte Eichtheorie aufgebaut werden kann. Dabei geht es mir hier nicht um den mathematischen Formalismus, diesen findet man z. B. bei (Tre 1). Vielmehr will ich -ähnlich wie bei der Gravitation- die anschauliche Bedeutung der Formeln erklären.
Bei diesem Unterfangen fallen sofort zwei wesentliche Unterschiede zwischen Gravitation und elektrischer Kraft auf:
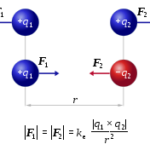
- Die Gravitation wirkt für alle Massen anziehend. Bei der elektrischen Kraft gibt es positive und negative Ladungen. Gleichnamige Ladungen stossen sich ab, unterschiedliche ziehen sich an.
- Im Gravitationsfeld werden alle Dinge gleich stark beschleunigt. Wie schon in Punkt 1 klar wird, ist dies bei der elektrischen Kraft nicht so.
Auf den ersten Blick würde man denken: Wenn die elektrische Kraft wie die Gravitation ein Effekt der Raumzeit wäre, müsste sie alle Teilchen gleich rasch in die gleiche Richtung beschleunigen. Denn alle Teilchen sind ja in der gleichen Raumzeit. Wie könnte es da unterschiedliche Beschleunigungen geben?
Schauen wir noch einmal die Erklärung zur Gravitation an. Die Gravitationskraft entsteht dadurch, dass die Zeit in der Nähe einer Masse langsamer läuft, wodurch die Geometrie der Raumzeit gekrümmt wird.
Abbildung 1 Anschauliche Erklärung der Gravitation: Ein Teilchen mit DurchmesserDx bewegt sich mit Lichtgeschwindigkeit durch die Zeit. Dabei wird es unten abgebremst. Wenn sich der obere Teil des Teilchens (pink) um cToben durch die Zeit bewegt, kommt der untere Teil (blau) nur cTunten. Dadurch wird das Teilchen auf einen Kreis mit dem Radius R gelenkt, wobei die Kreisbeschleunigung aKreis=c2/R ist.
Wie sieht dies nun im Fall der elektrischen Kraft aus? -In der Quantentheorie werden Teilchen durch Wellenfunktionen beschrieben. Eine Wellenfunktion ordnet jedem Punkt der 3+1 dimensionalen Raumzeit eine komplexe Zahl, die ‘Amplitude’, zu. Man könnte bei der Gravitation auch sagen: Unten ist die Periode 1/w der Wellenfunktion kürzer, deshalb wird das Teilchen nach unten beschleunigt.
In der Wellenfunktion steht unter anderem ein Faktor e-iwt oder eiwt. Der Faktor e-iwt bewirkt, dass sich die Amplitude der Welle im Lauf der Zeit in der komplexen Ebene im Uhrzeigersinn dreht. Der Faktor eiwt hat eine Drehung im Gegenuhrzeigersinn zur Folge. Die Frequenz w dieser Drehung hängt über die Unbestimmtheitsrelation mit der Energie, also mit der Masse des Teilchens zusammen.
Bei der elektrischen Kraft müssen wir das verschiedene Verhalten von positiven und negativen Ladungen erklären können. Genau dies leistet die sogenannte Eichtheorie. Der Faktor e-iwt gehört zu einer negativen Ladung, der Faktor eiwt zu einer positiven. Die Welle einer positiven Ladung dreht sich also in der komplexen Ebene im Gegenuhrzeigersinn. Wenn wir dies in einem Koordinatensystem mit der komplexen Ebene und der Zeit aufzeichnen, ergibt sich für eiwt eine rechtshändige Spirale.
Abbildung 2 Durch den Faktor eiwt dreht sich die Wellenfunktion einer positiven Ladung in der komplexen Ebene Gegenuhrzeigersinn. In jedem Punkt der Raumzeit müsste man sich eine komplexe Ebene vorstellen, in der sich die Amplitude der Welle dreht.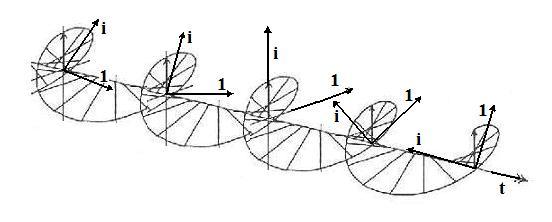
Die Wellenfunktion ist also eine Funktion, die jedem Punkt der Raumzeit eine komplexe Amplitude zuordnet. Diese komplexe Amplitude führt in jedem Punkt des Raumes die in Abbildung 2. gezeichnete Drehung durch, wobei sich die Länge der Amplitude normalerweise im Laufe der Zeit ändert.
Wir stellen uns also in jedem Punkt der Raumzeit eine komplexe Ebene vor. Die Frage ist nun, wie diese komplexen Ebenen relativ zueinander ausgerichtet werden. Die Amplitude eines Teilchens liegt zum Zeitpunkt t0 in einer anderen komplexen Ebene als zum Zeitpunkt t1. Woher weiss ich, ob sich die Amplitude gedreht hat oder ob die komplexe Ebene sich im Laufe der Zeit dreht?
Dies ist anschaulich der Gedankengang, der zur Eichtheorie der elektrischen Kraft führt. Die Richtung der Koordinatenachsen der komplexen Ebene muss geeicht werden. Dazu wird ein sogenanntes Eichfeld eingeführt, das jedem Punkt der Raumzeit eine komplexe Zahlenebene zuordnet. Je näher ein Punkt einer elektrischen Ladung ist, desto stärker wird dort die Eichung von der Drehung der Ladung beeinflusst. In der Nähe einer positiven Ladung drehen sich also die komplexen Ebenen wie die Ladung im Gegenuhrzeigersinn.
In der Nähe einer Ladung drehen sich die komplexen Ebenen in die gleiche Richtung wie die Ladung, aber weniger schnell. Wird nun eine Ladung mit gleichem Vorzeichen in dieses Feld gelegt, so dreht die Eichrichtung ständig davon. Es dauert daher länger, bis die Phase der Welle wieder im Grundzustand ist. Die Wellenlänge ist daher länger als im ungedrehten System.
Dies gilt aber nicht für alle Wellen. Dreht sich die Welle nämlich in die andere Richtung, (das bedeutet, dass die Ladung des Teilchens das umgekehrte Vorzeichen hat), wäre die Wellenlänge im Gegenteil verkürzt.
Wie wird nun die komplexe Ebene geeicht? Es gibt kein anderes Referenzsystem als die Teilchen, die sich in der Umgebung befinden. Drehen sich die Phasen dieser Teilchen mehrheitlich im Uhrzeigersinn, tragen sie also mehrheitlich positive Ladung, so wird sich auch das Eichfeld im Laufe der Zeit in dieser Richtung drehen. Die Wellenlängen der positiven Ladungen sind in so einem Gebiet also gedehnt, während die der negativen Ladungen gestaucht werden.
Stellen wir uns nun eine Wellenfront vor, deren oberer Teil sich mit einer Frequenz w dreht, während der untere Teil in einem Bereich liegt, in dem die komplexe Ebene sich im Laufe der Zeit in der gleichen Richtung davon dreht. Die Wellenlänge ist dann im unteren Bereich stärker gedehnt als im oberen. Wie im Artikel Gravitation gezeigt, wird jedes Teilchen in die Richtung gelenkt, in der ihre Wellenlänge möglichst kurz ist. Aus diesem Grund ziehen sich ungleichnamige Ladungen an, während sich gleichnamige abstossen.
Was geschieht mit neutralen Teilchen?
Teilchen ohne Ladung können als Überlagerung zweier unterschiedlicher Ladungen angesehen werden. Werden die Phasen e-iwt und eiwt überlagert, so ergibt sich:
e-iwt + eiwt = 2 cos wt
Diese Welle dreht sich nicht mehr in der komplexen Ebene, sondern ihre Amplitude verändert ihre Länge. Eine volle Periode ist durchlaufen, wenn die Amplitude zum zweiten Mal die ursprüngliche Länge hat. Damit ist aber die Wellenlänge eines neutralen Teilchens völlig unabhängig davon, wie das Eichfeld gedreht wird.
Wie hängt die Beschleunigung von der Masse ab?
Die Frequenz eines Teilchens hängt direkt proportional von seiner Masse ab. Analog zur Gravitation kann ich die Beschleunigung (Kreisbeschleunigung in der Raumzeit) berechnen.
Abbildung 4 Die Frequenz der Wellenfunktion einer positiven Ladung ist in der Nähe einer negativen Ladung grösser als weiter entfernt. Wie bei der Gravitation stelle ich mir vor, dass die Welle sich mit der Lichtgeschwindigkeit c auf der Zeitachse ausbreitet. Von den Raumdimensionen ist nur die x-Richtung gezeichnet, also die Achse, auf der die zwei Ladungen liegen.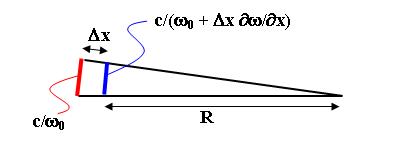
Achtung: R ist nicht der Abstand zwischen den Ladungen (vielleicht sind ja auch mehr als zwei Ladungen im Spiel), sondern Radius, der zur momentanen Beschleunigung des Teilchens in der Raumzeit gehört.
dw/dx gibt an, wie stark die Frequenz zunimmt, wenn ich mich in x-Richtung bewege. Nach dem Strahlensatz gilt:
c/w0(R + Dx) = c/(w0 + Dx dw/dx)R
Für die Kreisbeschleunigung c2/R erhält man:
c2/R = c2/w0 · dw/dx
Die Beschleunigung ist also umgekehrt proportional zur Frequenz und damit auch zur Masse des Teilchens. Das heisst:
Ein Teilchen wird k mal so stark beschleunigt wie ein gleich geladenes Teilchen, das eine k mal so grosse Masse hat.
Wozu ist das gut?
Was könnte der Nutzen eines solchen Modells sein? -Ich betone noch einmal, dass ich keine neue Physik geschaffen habe. Die obige Beschreibung ist der üblichen Herleitung der Elektrodynamik als Eichtheorie nachempfunden. Wenn das obige Modell in irgendeinem Punkt nicht zum gleichen Resultat führt, ist mein Modell falsch, denn die Quantenelektrodynamik ist extrem gut bestätigt.
Obwohl ich nichts Neues geschaffen habe, scheint mir die Veranschaulichung doch zumindest didaktisch wertvoll. Einige Elemente in den Formeln der Elektrodynamik scheinen auf den ersten Blick ziemlich willkürlich. So braucht man zwar das Minuszeichen der elektrischen Ladung, damit die Formeln die Realität richtig beschreiben, aber es scheint ziemlich rätselhaft, wie dieses Minus in der Realität verwirklicht sein könnte. Mein Modell zeigt, dass dies überhaupt nicht geheimnisvoll sein muss.
Zweitens bin ich der Ansicht, dass wir immer versuchen sollten, so viele passende Modelle wie möglich im Hinterkopf zu haben, wenn wir theoretische Forschung betreiben. Viele Physiker denken heute rein mathematisch. Sie begnügen sich damit, die Dinge ausrechnen zu können und verzichten gänzlich auf Modelle. Wenn ich aber die Texte grosser Physiker, wie Einstein oder Feynmann lese, so fällt mir immer wieder auf, wie sehr sie versuchen, Modelle zu sehen, statt nur mit abstrakten Mathematischen Regeln zu operieren. Ich denke, Modelle sehen zu können, ist eine enorme zusätzliche Kraft, wenn man die Physik verstehen will.
Ich erlaube mir, dazu Feynmann zu zitieren (Fey 3):
Die Topologie war für die Mathematiker durchaus nicht offensichtlich. Es gab allerlei verrückte Möglichkeiten, die ”unanschaulich” waren. Dann hatte ich einen Einfall. Ich forderte sie heraus. “Ich wette, ihr könnt mir nicht ein einziges Theorem nennen – und zwar die Annahmen und das Theorem in Begriffen, die ich verstehen kann – bei dem ich euch nicht auf der Stell sagen kann, ob es zutrifft oder falsch ist.”
Das lief oft so: Sie erklärten mir: “Du hast eine Orange, o. k.? Nun schneidest du die Orange in unendlich viele Stücke, setzt sie wieder zusammen, und sie ist so gross wie die Sonne. Wahr oder falsch?”
“Keine Löcher?”
“Keine Löcher.”
“Unmöglich! So etwas gibt´s nicht.”
“Ha! Wir haben ihn! Kommt mal alle her! Es ist Soundsos Theorem des unmessbaren Masses!”
Genau dann, wenn sie meinen, sie hätten mich, erinnere ich sie: “Aber ihr habt doch von einer Orange gesprochen! Man kann die Orangenschale nicht dünner schneiden als die Atome.”
“Aber wir haben die Bedingung der Kontinuität: Wir können immer kleiner schneiden!”
“Nein, ihr habt von einer Orange gesprochen, also habe ich angenommen, dass ihr eine wirkliche Orange gemeint habt.”
Auf diese Weise gewann ich immer. Wenn ich richtig riet, grossartig! Riet ich falsch, dann konnte ich immer etwas in ihren Vereinfachungen finden, das sie ausgelassen hatten.
Tatsächlich war an meinen Vermutungen wirklich etwas dran. Ich folgte einem Schema, das ich noch heute benutze, wenn mir jemand etwas erklärt, das ich zu verstehen versuche: ich denke mir Beispiele aus. Die Mathematiker kamen zum Beispiel mit einem tollen Theorem an, und sie sind ganz aufgeregt. Während sie mir die Bedingungen des Theorems nennen, konstruiere ich etwas, das alle Bedingungen erfüllt. Etwa so: Gegeben sei eine Menge (eine Kugel) – und die Menge sei disjunkt (zwei Kugeln). Dann stelle ich mir vor, dass die Kugeln farbig werden, dass sie Haare bekommen oder sonstwas, während die Mathematiker immer mehr Bedingungen stellen. Schliesslich tragen sie das Theorem vor, und das ist dann irgendwas Dummes über die Kugel, was für mein haariges grünes Kugel-Ding nicht zutrifft, also sage ich: “Falsch!”
…
Meistens riet ich richtig, denn obwohl die Mathematiker meinten, ihre Topologie-Theoreme seien unanschaulich, waren sie eigentlich nicht so schwierig, wie sie aussahen.
Weiterführende Artikel auf dieser Homepage:
Gravitation
Die Maxwell-Gleichungen
Weiterführende Literatur
Philip Wehrli, ‘Das Universum, das Ich und der liebe Gott’, (2017), Nibe Verlag,

In diesem Buch präsentiere ich einen Gesamtüberblick über mein Weltbild: Wie ist das Universum entstanden? Wie ist das Leben auf der Erde entstanden? Was ist Bewusstsein und woher kommt es? Braucht es dazu einen Gott?
Viele Artikel dieses Blogs werden in diesem Buch in einen einheitlichen Rahmen gebracht, so dass sich ein (ziemlich) vollständiges Weltbild ergibt.
Leserunde bei Lovelybooks zum Buch ‘Das Universum, das Ich und der liebe Gott’, von Philipp Wehrli (abgeschlossen)
Rezensionen bei Lovelybooks
Rezensionen bei Amazon
Film-Präsentation zum Buch
Nibe Verlag